Hostname: page-component-586b7cd67f-dsjbd Total loading time: 0 Render date: 2024-11-28T08:15:27.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Topology and geometry of nontrivial rank-one convex hulls for two-by-two matrices

Published online by Cambridge University Press:  22 March 2006

Carl-Friedrich Kreiner  and
Johannes Zimmer
Carl-Friedrich Kreiner
Affiliation:
Max Planck Institute for Mathematics in the Sciences, Inselstr. 22, 04 103 Leipzig, Germany.
Johannes Zimmer
Affiliation:
University of Bath, Department of Mathematical Sciences, Claverton Down, Bath BA2 7AY, UK; [email protected]
Get access

Abstract

Continuing earlier work by Székelyhidi, we describe the topological and geometric structure of so-called T 4-configurations which are the most prominent examples of nontrivial rank-one convex hulls. It turns out that the structure of T 4-configurations in $\mathbb{R}^{2\times 2}$ 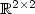is very rich; in particular, their collection is open as a subset of $(\mathbb{R}^{2\times2})^{4}$ 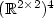. Moreover a previously purely algebraic criterion is given a geometric interpretation. As a consequence, we sketch an improved algorithm to detect T 4-configurations.

Keywords

Rank-one convexityT 4-configurations.
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 12 , Issue 2 , April 2006 , pp. 253 - 270
Copyright
© EDP Sciences, SMAI, 2006

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aranda, E. and Pedregal, P., On the computation of the rank-one convex hull of a function. SIAM J. Sci. Comput. 22 (2000) 1772–1790 (electronic). CrossRef
Aubry, S., Fago, M. and Ortiz, M., A constrained sequential-lamination algorithm for the simulation of sub-grid microstructure in martensitic materials. Comput. Methods Appl. Mech. Engrg. 192 (2003) 2823–2843. CrossRef
Chlebík, M. and Kirchheim, B., Rigidity for the four gradient problem. J. Reine Angew. Math. 551 (2002) 1–9. CrossRef
B. Dacorogna, Direct methods in the calculus of variations. Applied Mathematical Sciences, Springer-Verlag, Berlin 78 (1989).
Dolzmann, G., Numerical computation of rank-one convex envelopes. SIAM J. Numer. Anal. 36 (1999) 1621–1635 (electronic). CrossRef
Da.R. Grayson and M.E. Stillman, Macaulay 2, a software system for research in algebraic geometry. Available at http://www.math.uiuc.edu/Macaulay2/
J. Harris, Algebraic geometry. Springer-Verlag, New York (1995). A first course, Corrected reprint of the 1992 original.
B. Kirchheim, Rigidity and geometry of microstructures. Lecture notes 16/2003, Max Planck Institute for Mathematics in the Sciences, Leipzig (2003).
B. Kirchheim, S. Müller and V. Šverák, Studying nonlinear pde by geometry in matrix space, in Geometric analysis and nonlinear partial differential equations. Springer, Berlin (2003) 347–395.
C.-F. Kreiner, Algebraic methods for convexity notions in the calculus of variations. Master's thesis, Technische Universität München, Zentrum Mathematik (2003).
Kreiner, C.-F., Zimmer, J. and Chenchiah, I., Towards the efficient computation of effective properties of microstructured materials. Comptes Rendus Mecanique 332 (2004) 169–174. CrossRef
Matoušek, J. and Plecháč, P., On functional separately convex hulls. Discrete Comput. Geom. 19 (1998) 105–130. CrossRef
S. Müller, Variational models for microstructure and phase transitions, in Calculus of variations and geometric evolution problems (Cetraro, 1996). Springer, Berlin, Lect. Notes Math. 1713 (1999) 85–210.
S. Müller and V. Šverák, Unexpected solutions of first and second order partial differential equations, in Proceedings of the International Congress of Mathematicians, Vol. II (Berlin, 1998), Extra Vol. II (1998) 691–702.
L. Råde and B. Westergren, Mathematics handbook for science and engineering. Springer-Verlag, Berlin, fourth edition (1999).
V. Scheffer, Regularity and irregularity of solutions to nonlinear second order elliptic systems of partial differential equations and inequalities. Ph.D. thesis, Princeton University (1974).
Šverák, V., Rank-one convexity does not imply quasiconvexity. Proc. Roy. Soc. Edinburgh Sect. A 120 (1992) 185–189. CrossRef
Székelyhidi Jr, L., Rank-one convex hulls in $\Bbb R\sp {2\times 2}$ . Calc. Var. Partial Differ. Equ. 22 (2005) 253–281.
L. Tartar, Some remarks on separately convex functions, in Microstructure and phase transition. Springer, New York, IMA Vol. Math. Appl. 54 (1993) 191–204.