Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-17T07:51:14.609Z Has data issue: false hasContentIssue false
  • English
  • Français

Oscillations and concentrations in sequences of gradients

Published online by Cambridge University Press:  21 September 2007

Agnieszka Kałamajska  and
Martin Kružík
Agnieszka Kałamajska
Affiliation:
Institute of Mathematics, Warsaw University, ul. Banacha 2, 02-097 Warsaw, Poland; [email protected]
Martin Kružík
Affiliation:
Institute of Information Theory and Automation, Academy of Sciences of the Czech Republic. Corresponding address Pod vodárenskou věží 4, 182 08 Praha 8, Czech Republic. Faculty of Civil Engineering, Czech Technical University, Thákurova 7, 166 29 Praha 6, Czech Republic; [email protected] (corresponding author).
Get access

Abstract

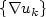We use DiPerna's and Majda's generalization of Young measures to describe oscillations and concentrations in sequences of gradients, $\{\nabla u_k\}$ , bounded in $L^p(\Omega;{\mathbb R}^{m\times n})$ 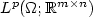if p > 1 and $\Omega\subset{\mathbb R}^n$ 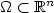is a bounded domain with the extension property in $W^{1,p}$ 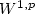.Our main result is a characterization of those DiPerna-Majda measures which are generated by gradients of Sobolev maps satisfying the same fixed Dirichlet boundary condition. Caseswhere no boundary conditions nor regularity of Ω arerequired and links with lower semicontinuity results by Meyers andby Acerbi and Fusco are also discussed.

Keywords

Sequences of gradientsconcentrationsoscillationsquasiconvexity
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 14 , Issue 1 , January 2008 , pp. 71 - 104
Copyright
© EDP Sciences, SMAI, 2007

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Acerbi, E. and Fusco, N., Semicontinuity problems in the calculus of variations. Arch. Rational Mech. Anal. 86 (1984) 125–145. CrossRef
Alibert, J.J. and Bouchitté, G., Non-uniform integrability and generalized Young measures. J. Convex Anal. 4 (1997) 125–145.
Allard, W., On the first variation of a varifold. Ann. Math. 95 (1972) 417–491. CrossRef
Almgren Jr, F.J.., Existence and regularity almost everywhere of solutions to elliptic variational problems among surfaces of varying topological type and singularity structure. Ann. Math. 87 (1968) 321–391. CrossRef
J.M. Ball, A version of the fundamental theorem for Young measures, in PDEs and Continuum Models of Phase Transition, M. Rascle, D. Serre and M. Slemrod Eds., Lect. Notes Phys. 344, Springer, Berlin (1989) 207–215.
Ball, J.M and Murat, F., $W^{1,p}$ -quasiconvexity and variational problems for multiple integrals. J. Funct. Anal. 58 (1984) 225–253. CrossRef
P. Billingsley, Probability and Measure. 3rd edn., John Wiley & Sons Ltd., Chichester (1995).
B. Dacorogna, Direct Methods in the Calculus of Variations. Springer, Berlin (1989).
DiPerna, R.J. and Majda, A.J., Oscillations and concentrations in weak solutions of the incompressible fluid equations. Commun. Math. Phys. 108 (1987) 667–689. CrossRef
N. Dunford and J.T. Schwartz, Linear Operators, Part I. Interscience, New York (1967).
R. Engelking, General topology. 2nd edn., PWN, Warszawa (1985).
L.C. Evans and R.F. Gariepy, Measure Theory and Fine Properties of Functions. CRC Press, Inc. Boca Raton (1992).
Fonseca, I., Lower semicontinuity of surface energies. Proc. Roy. Soc. Edinburgh 120A (1992) 95–115.
Fonseca, I. and Müller, S., Pedregal, P., Analysis of concentration and oscillation effects generated by gradients. SIAM J. Math. Anal. 29 (1998) 736–756. CrossRef
Greco, L., Iwaniec, T. and Subramanian, U., Another approach to biting convergence of Jacobians. Illin. Journ. Math. 47 (2003) 815–830.
M. de Guzmán, Differentiation of integrals in ${\mathbb R}^n$ , Lecture Notes in Math. 481. Springer, Berlin (1975).
Hafsa, O.M, Mandallena, J.-P. and Michaille, G., Homogenization of periodic nonconvex integral functionals in terms of Young measures. ESAIM: COCV 12 (2006) 35–51. CrossRef
Kałamajska, A., On lower semicontinuity of multiple integrals. Coll. Math. 74 (1997) 71–78.
Kałamajska, A., Young, On measures controlling discontinuous functions. J. Conv. Anal. 13 (2006) 177–192.
A. Kałamajska and M. Kružík, On weak lower semicontinuity of integral functionals along concentrating sequences (in preparation).
Kinderlehrer, D. and Pedregal, P., Characterization of Young measures generated by gradients. Arch. Rat. Mech.Anal. 115 (1991) 329–365. CrossRef
Kinderlehrer, D. and Pedregal, P., Gradient Young measures generated by sequences in Sobolev spaces. J. Geom. Anal. 4 (1994) 59–90. CrossRef
J. Kristensen, Finite functionals and Young measures generated by gradients of Sobolev functions. Mat-report 1994-34, Math. Institute, Technical University of Denmark (1994).
Kristensen, J., Lower semicontinuity in spaces of weakly differentiable functions. Math. Ann. 313 (1999) 653–710. CrossRef
Kružík, M. and Roubíček, T., On the measures of DiPerna and Majda. Mathematica Bohemica 122 (1997) 383–399.
Kružík, M. and Roubíček, T., Optimization problems with concentration and oscillation effects: relaxation theory and numerical approximation. Numer. Funct. Anal. Optim. 20 (1999) 511–530. CrossRef
C. Licht, G. Michaille and S. Pagano, A model of elastic adhesive bonded joints through oscillation-concentration measures. Prépublication of the Institut de Mathématiques et de Modélisation de Montpellier, UMR-CNRS 5149.
Marcellini, P., Approximation of quasiconvex functions and lower semicontinuity of multiple integrals. Manuscripta Math. 51 (1985) 1–28. CrossRef
V.G. Mazja, Sobolev Spaces. Springer, Berlin (1985).
Meyers, N.G., Quasi-convexity and lower semicontinuity of multiple integrals of any order. Trans. Am. Math. Soc. 119 (1965) 125–149. CrossRef
C.B. Morrey, Multiple Integrals in the Calculus of Variations. Springer, Berlin (1966).
Müller, S., Variational models for microstructure and phase transisions. Lecture Notes in Mathematics 1713 (1999) 85–210. CrossRef
P. Pedregal, Parametrized Measures and Variational Principles. Birkäuser, Basel (1997).
Reshetnyak, Yu.G., The generalized derivatives and the a.e. differentiability. Mat. Sb. 75 (1968) 323–334 (in Russian).
Reshetnyak, Yu.G., Weak convergence and completely additive vector functions on a set. Sibirsk. Mat. Zh. 9 (1968) 1039–1045. CrossRef
T. Roubíček, Relaxation in Optimization Theory and Variational Calculus. W. de Gruyter, Berlin (1997).
Schonbek, M.E., Convergence of solutions to nonlinear dispersive equations. Comm. Part. Diff. Equa. 7 (1982) 959–1000.
E.M. Stein, Singular Integrals and Differentiability Properties of Functions. Princeton university Press, Princeton (1970).
L. Tartar, Compensated compactness and applications to partial differential equations, in Nonlinear Analysis and Mechanics, R.J. Knops Ed., Heriott-Watt Symposium IV, Pitman Res. Notes Math. 39, San Francisco (1979).
L. Tartar, Mathematical tools for studying oscillations and concentrations: From Young measures to H-measures and their variants, in Multiscale problems in science and technology. Challenges to mathematical analysis and perspectives, N. Antonič et al. Eds., Proceedings of the conference on multiscale problems in science and technology, held in Dubrovnik, Croatia, September 3–9, 2000, Springer, Berlin (2002).
M. Valadier, Young measures, in Methods of Nonconvex Analysis, A. Cellina Ed., Lect. Notes Math. 1446, Springer, Berlin (1990) 152–188.
J. Warga, Optimal Control of Differential and Functional Equations. Academic Press, New York (1972).
L.C. Young, Generalized curves and the existence of an attained absolute minimum in the calculus of variations. Comptes Rendus de la Société des Sciences et des Lettres de Varsovie, Classe III 30 (1937) 212–234.