No CrossRef data available.
Article contents
On the continuity of degenerate n-harmonicfunctions
Published online by Cambridge University Press: 14 September 2011
Abstract
We study the regularity of finite energy solutions to degeneraten-harmonic equations. The functionK(x), which measures the degeneracy, is assumed to besubexponentially integrable, i.e. it verifies the condition exp(P(K)) ∈ Lloc1. The function P(t) is increasing on [0,∞[ and satisfies the divergence condition \begin{equation}\int_1^\infty\frac{P(t)}{t^2}\,{\rm d}t=\infty.\end{equation}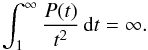
∫1∞P(t)t2 dt=∞.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 18 , Issue 3 , July 2012 , pp. 621 - 642
- Copyright
- © EDP Sciences, SMAI, 2011
References
E. Acerbi and N. Fusco, An approximation lemma for W 1,p functions, in Material Instabilities in Continuum Mechanics, J.M. Ball Ed. (Edinburgh, 1985–1986). Oxford University Press, New York (1988).
Carozza, M., Moscariello, G. and Napoli, A. Passarelli di, Regularity for p-harmonic equations with right hand side in Orlicz-Zygmund classes. J. Differ. Equ. 242 (2007) 248–268. Google Scholar
Gehring, F., Rings and quasiconformal mapping in the space. Trans. Amer. Math. Soc. 103 (1962) 353–393. Google Scholar
Giannetti, F. and Passarelli di Napoli, A., Isoperimetric type inequalities for differential forms on manifolds. Indiana Univ. Math. J. 54 (2005) 1483–1497. Google Scholar
Giannetti, F. and Passarelli di Napoli, A., On very weak solutions of degenerate equations. NoDEA 14 (2007) 739–751. Google Scholar
Giannetti, F., Greco, L. and Passarelli di Napoli, A., The self-improving property of the Jacobian determinant in Orlicz spaces. Indiana Univ. Math. J. 59 (2010) 91–114. Google Scholar
Giannetti, F., Greco, L. and Passarelli di Napoli, A., Regularity of solutions of degenerate A-harmonic equations. Nonlinear Anal. 73 (2010) 2651–2665. Google Scholar
Iwaniec, T. and Onninen, J., Continuity estimates for n-harmonic equations. Indiana Univ. Math. J. 56 (2007) 805–824. Google Scholar
Iwaniec, T. and Sbordone, C., Quasiharmonic fields. Ann. Inst. Henri Poincaré Anal. non Linéaire 18 (2001) 519–572. Google Scholar
Iwaniec, T., Migliaccio, L., Moscariello, G. and Passarelli di Napoli, A., A priori estimates for nonlinear elliptic complexes. Advances Difference Equ. 8 (2003) 513–546. Google Scholar
Kauhanen, J., Koskela, P., Maly, J., Onninen, J. and Zhong, X., Mappings of finite distortion : sharp Orlicz conditions. Rev. Mat. Iberoamericana 19 (2003) 857–872. Google Scholar
Koskela, P. and Onninen, J., Mappings of finite distortion : the sharp modulus of continuity. Trans. Amer. Math. Soc. 355 (2003) 1905–1920. Google Scholar
Koskela, P., Manfredi, J. and Villamor, E., Regularity theory and traces of 𝒜-harmonic functions. Trans. Amer. Math. Soc. 348 (1996) 755–766. Google Scholar
M.A. Krasnosel’skii and Ya.B. Rutickii, Convex Functions and Orlicz Spaces. P. Noordhoff LTD, Groningen, The Netherlands (1961).
Lewis, J., On very weak solutions of certain elliptic systems. Commun. Partial. Differ. Equ. 18 (1993) 1515–1537. Google Scholar
Moscariello, G., On the integrability of “finite energy” solutions for p-harmonic equations. NoDEA 11 (2004) 393–406. Google Scholar
M.M. Rao and Z.D. Ren, Theory of Orlicz spaces. Monographs and Textbooks in Pure and Applied Mathematics 146. Marcel Dekker, Inc., New York (1991).
G. Stampacchia, Équations elliptiques du second ordre à coefficients discontinus. Semin. de Math. Supérieures 16, Univ. de Montréal (1966).