Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-24T09:00:49.594Z Has data issue: false hasContentIssue false
  • English
  • Français

On indecomposable sets with applications

Published online by Cambridge University Press:  28 March 2014

Andrew Lorent
Andrew Lorent*
Affiliation:
Mathematics Department, University of Cincinnati, 2600 Clifton Ave. Cincinnati OH 45221.. [email protected]
Get access

Abstract

In this note we show the characteristic function of every indecomposable setF in theplane is BVequivalent to the characteristic function a closed set See Formula in PDF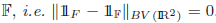\hbox{See Formula in PDF} .We show by example this is false in dimension three and above. As a corollary to thisresult we show that for every ϵ > 0 a set of finite perimeter S can be approximated by aclosed subset See Formula in PDF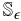\hbox{See Formula in PDF} with finitely many indecomposablecomponents and with the property that See Formula in PDF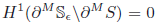\hbox{See Formula in PDF} and See Formula in PDF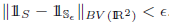\hbox{See Formula in PDF} .We apply this corollary to give a short proof that locally quasiminimizing sets in theplane are BVlextension domains.

Keywords

Sets of finite perimeterindecomposable sets
Type
Research Article
Information
ESAIM: Control, Optimisation and Calculus of Variations , Volume 20 , Issue 2 , April 2014 , pp. 612 - 631
Copyright
© EDP Sciences, SMAI, 2014

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

L. Ambrosio, N. Fusco and D. Pallara, Functions of bounded variation and free discontinuity problems. Oxford Mathematical Monographs. The Clarendon Press, Oxford University Press, New York (2000).
Ambrosio, L., Caselles, V., Masnou, S. and Morel, J.-M., Connected components of sets of finite perimeter and applications to image processing. J. Eur. Math. Soc. (JEMS) 3 (2001) 39–92. Google Scholar
Baldi, A. and Montefalcone, F., A note on the extension of BV functions in metric measure spaces. J. Math. Anal. Appl. 340 (2008) 197–208. Google Scholar
Yu. Burago and V.G. Maz’ya, Potential theory and function theory for irregular regions. Translated from Russian. Seminars in Mathematics. Vol. 3. of V.A. Steklov Mathematical Institute, Leningrad, Consultants Bureau, New York (1969).
David, G. and Semmes, S., Quasiminimal surfaces of codimension 1 and John domains. Pacific J. Math. 183 (1998) 213–277. Google Scholar
Kinnunenm, J., Korte, R., Lorent, A. and Shanmugalingam, N., Regularity of sets with quasiminimal boundary surfaces in metric spaces. J. Geom. Anal. 23 (2013) 1607–1640. Google Scholar
B. Kirchheim, Lipschitz minimizers of the 3-well problem having gradients of bounded variation. MIS. MPg. Preprint (12/1998).
P. Mattila, Geometry of sets and measures in Euclidean spaces. Fractals and rectifiability. Vol. 44. of Cambridge Studies in Advanced Mathematics. Cambridge University Press, Cambridge (1995).