Article contents
A note on convergence of low energy critical pointsof nonlinear elasticity functionals,for thin shells of arbitrary geometry
Published online by Cambridge University Press: 24 March 2010
Abstract
We prove that the critical points of the 3d nonlinear elasticity functionalon shells of small thickness h and around the mid-surface S of arbitrary geometry, converge as h → 0to the critical points of the vonKármán functional on S, recently proposed in [Lewicka et al., Ann. Scuola Norm. Sup. Pisa Cl. Sci. (to appear)].This result extends the statement in [Müller and Pakzad, Comm. Part. Differ. Equ. 33 (2008) 1018–1032], derived for the case of plates when $S\subset\mathbb{R}^2$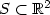 .The convergence holds provided the elastic energies of the 3d deformations scale like h4 and the external body forces scale like h3.
.The convergence holds provided the elastic energies of the 3d deformations scale like h4 and the external body forces scale like h3.
- Type
- Research Article
- Information
- ESAIM: Control, Optimisation and Calculus of Variations , Volume 17 , Issue 2 , April 2011 , pp. 493 - 505
- Copyright
- © EDP Sciences, SMAI, 2010
References
- 10
- Cited by


