Nonlinear diffusion equations with variable coefficients as gradient flows in Wasserstein spaces

Abstract

We study existence and approximation of non-negative solutions of partial differential equations of the type 
 $$\partial_t u - \div (A(\nabla (f(u))+u\nabla V )) = 0 \qquad \mbox{in } (0,+\infty )\times \mathbb{R}^n,\qquad\qquad (0.1)$$ where A is a symmetric matrix-valued function of the spatial variable satisfying a uniform ellipticity condition, $f:[0,+\infty) \rightarrow[0,+\infty)$ 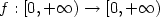is a suitable non decreasing function, $V:\mathbb{R}^n \rightarrow\mathbb{R}$ 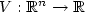is a convex function.Introducing the energy functional $\phi(u)=\int_{\mathbb{R}^n} F(u(x))\,{\rm d}x+\int_{\mathbb{R}^n}V(x)u(x)\,{\rm d}x$ 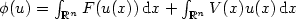,where F is a convex function linked to f by $f(u) = uF'(u)-F(u)$ 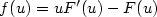,we show that u is the “gradient flow” of ϕ with respect to the2-Wasserstein distance between probability measures onthe space $\mathbb{R}^n$ 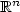, endowed with the Riemannian distance induced by $A^{-1}.$ 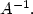In the case of uniform convexity of V, long time asymptotic behaviour and decay rate to the stationary statefor solutions of equation (0.1) are studied.A contraction property in Wasserstein distance for solutions of equation (0.1)is also studied in a particular case.