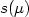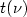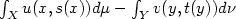Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Ekeland, Ivar
2010.
Existence, uniqueness and efficiency of equilibrium in hedonic markets with multidimensional types.
Economic Theory,
Vol. 42,
Issue. 2,
p.
275.
Carlier, G.
and
Ekeland, I.
2010.
Matching for teams.
Economic Theory,
Vol. 42,
Issue. 2,
p.
397.
Chiappori, Pierre-André
McCann, Robert J.
and
Nesheim, Lars P.
2010.
Hedonic price equilibria, stable matching, and optimal transport: equivalence, topology, and uniqueness.
Economic Theory,
Vol. 42,
Issue. 2,
p.
317.
Carlier, G.
and
Lachapelle, A.
2011.
A Planning Problem Combining Calculus of Variations and Optimal Transport.
Applied Mathematics & Optimization,
Vol. 63,
Issue. 1,
p.
1.
Kitagawa, Jun
and
Warren, Micah
2012.
Regularity for the Optimal Transportation Problem with Euclidean Distance Squared Cost on the Embedded Sphere.
SIAM Journal on Mathematical Analysis,
Vol. 44,
Issue. 4,
p.
2871.
Pass, Brendan
2013.
Regularity properties of optimal transportation problems arising in hedonic pricing models.
ESAIM: Control, Optimisation and Calculus of Variations,
Vol. 19,
Issue. 3,
p.
668.
Ghoussoub, Nassif
and
Moameni, Abbas
2014.
Optimal mass transport and symmetric representations of their cost functions.
Mathematics and Financial Economics,
Vol. 8,
Issue. 4,
p.
435.
Mazón, José M.
Rossi, Julio D.
and
Toledo, Julián
2014.
An Optimal Matching Problem for the Euclidean Distance.
SIAM Journal on Mathematical Analysis,
Vol. 46,
Issue. 1,
p.
233.
Kim, Ju Hyun
2014.
Identifying the Distribution of Treatment Effects under Support Restrictions.
SSRN Electronic Journal,
Mazón, J. M.
Rossi, Julio D.
and
Toledo, J.
2014.
Optimal matching problems with costs given by Finsler distances.
Communications on Pure and Applied Analysis,
Vol. 14,
Issue. 1,
p.
229.
Pass, Brendan
2014.
Multi-marginal optimal transport and multi-agent matching problems: Uniqueness and structure of solutions.
Discrete & Continuous Dynamical Systems - A,
Vol. 34,
Issue. 4,
p.
1623.
Pass, Brendan
2015.
Multi-marginal optimal transport: Theory and applications.
ESAIM: Mathematical Modelling and Numerical Analysis,
Vol. 49,
Issue. 6,
p.
1771.
Igbida, Noureddine
Nguyen, Van Thanh
and
Toledo, Julián
2017.
On the Uniqueness and Numerical Approximations for a Matching Problem.
SIAM Journal on Optimization,
Vol. 27,
Issue. 4,
p.
2459.
Guillen, Nestor
and
Kitagawa, Jun
2017.
Pointwise Estimates and Regularity in Geometric Optics and Other Generated Jacobian Equations.
Communications on Pure and Applied Mathematics,
Vol. 70,
Issue. 6,
p.
1146.
Dizdar, Deniz
2018.
Two-Sided Investment and Matching with Multidimensional Cost Types and Attributes.
American Economic Journal: Microeconomics,
Vol. 10,
Issue. 3,
p.
86.
Mazón, J. M.
Rossi, J. D.
and
Toledo, J.
2018.
An optimal matching problem with constraints.
Revista Matemática Complutense,
Vol. 31,
Issue. 2,
p.
407.
Pass, Brendan
2019.
Interpolating between matching and hedonic pricing models.
Economic Theory,
Vol. 67,
Issue. 2,
p.
393.
Nenna, Luca
and
Pass, Brendan
2020.
Variational problems involving unequal dimensional optimal transport.
Journal de Mathématiques Pures et Appliquées,
Vol. 139,
Issue. ,
p.
83.
Tupitsa, Nazarii
Dvurechensky, Pavel
Gasnikov, Alexander
and
Uribe, Cesar A.
2020.
Multimarginal Optimal Transport by Accelerated Alternating Minimization.
p.
6132.
Coulson, N. Edward
Dong, Zhi
and
Sing, Tien Foo
2021.
Estimating Supply Functions for Residential Real Estate Attributes.
Real Estate Economics,
Vol. 49,
Issue. 2,
p.
397.