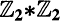We study a new topological classification of suspension flows on subshifts of finite type, and obtain a new proof of a theorem of Boyle's which states that, in an appropriate sense, all such flows are alike. We prove that the stochastic version of this classification is non-trivial by exhibiting a certain invariant, and show that this invariant is complete in a particular case, although not in general. Symbolic flows are important as models of basic sets of Axiom A flows, and so we discuss the significance of our results for this latter type of flow.

Let Ω be a totally disconnected compact metrizable space, and let α be a minimal homeomorphism of Ω. Let σ be a homeomorphism of order 2 on Ω such that ασ = σα−1, and assume that σ or ασ has a fixed point. We prove (Theorem 3.5) that the crossed product is an AF-algebra.

Let G be an abstract finite group. For an action α of G on a shift of finite type (SFT) S we introduce the periodic data of α, a computable finite-ordered set of complex polynomials. We show that two actions of G on possibly different SFTs are conjugate on periodic points iff their periodic data coincide. For each subgroup H of G the points fixed by α|H (the restriction of α to H) form a subsystem of S, which is of finite type. Our result shows that the zeta functions of these subsystems determine the conjugacy class (on periodic points) of α up to finitely many possibilities.

The orbit space of a finite skew action on an SFT S, endowed with the homeomorphism induced by S, is shown to have a zeta function equal to the zeta function of an SFT which is a left-closing quotient of S. We show that this zeta function equals the zeta function of S iff the skew action is inert with respect to a certain power of S.

Finally we consider functions of the periodic data as for example gyration numbers.

For a certain pair of discrete measured ergodic equivalence relations, we specify how one is imbedded into the other and obtain a factor and its subfactor. For this pair of factors index theory is developed. We obtain an index formula, an ‘extended’ relation corresponding to the basic extension, and so on. Our formulas as well as construction are very explicit and are given in terms of ‘measure theoretic’ data. We also present examples showing the contrast between type III0 index theory and type II1 (or IIIλ) index theory.

Let f be an Axiom A diffeomorphism, Ω its non wandering set, µ the Gibbs measure for the Lipschitz continuous potential. We consider the (suitably normalized) return times of the orbit to the ε-neighborhood of a point z ∈ Ω and prove that for µ-a.e. z the sequence of the normalized return times converges to the Poisson point process in finite dimensional distribution as ε → 0.

In this paper, we determine properties that a Lyapunov graph must satisfy for it to be associated with a gradient-like flow on a closed orientable three-manifold. We also address the question of the realization of abstract Lyapunov graphs as gradient-like flows on three-manifolds and as a byproduct we prove a partial converse to the theorem which states the Morse inequalities for closed orientable three-manifolds. We also present cancellation theorems of non-degenerate critical points for flows which arise as realizations of canonical abstract Lyapunov graphs.

For Fuchsian groups of the first kind containing parabolic elements, it is shown that the action on a suitable disconnection of the limit circle generates a Cuntz—Krieger C*-algebra. This clarifies and generalizes the situation of the subalgebra within O2, and provides a new proof of the simplicity and nuclearity of certain Cuntz—Krieger algebras. The proof relies on the Markov partition obtained from a suitable fundamental polygon for the group. Counter examples are given if an unsuitable fundamental polygon is used.