Research Article
Random products of automorphisms of Heisenberg nilmanifolds and Weil’s representation
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1277-1286
-
- Article
- Export citation
Generic super-exponential stability of invariant tori in Hamiltonian systems
-
- Published online by Cambridge University Press:
- 13 October 2010, pp. 1287-1303
-
- Article
- Export citation
Topological and symbolic dynamics for hyperbolic systems with holes
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1305-1323
-
- Article
- Export citation
A full family of multimodal maps on the circle
-
- Published online by Cambridge University Press:
- 20 July 2010, pp. 1325-1344
-
- Article
- Export citation
Approximating invariant densities of metastable systems
-
- Published online by Cambridge University Press:
- 02 September 2010, pp. 1345-1361
-
- Article
- Export citation
Extreme value theory and return time statistics for dispersing billiard maps and flows, Lozi maps and Lorenz-like maps
-
- Published online by Cambridge University Press:
- 30 June 2011, pp. 1363-1390
-
- Article
- Export citation
Hénon-like maps with arbitrary stationary combinatorics
-
- Published online by Cambridge University Press:
- 09 March 2011, pp. 1391-1443
-
- Article
- Export citation
Uniform sets and super-stationary sets over general alphabets
-
- Published online by Cambridge University Press:
- 14 March 2011, pp. 1445-1461
-
- Article
- Export citation
On maximal pattern complexity of some automatic words
-
- Published online by Cambridge University Press:
- 13 October 2010, pp. 1463-1470
-
- Article
- Export citation
Complete orbits for twist maps on the plane: the case of small twist
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1471-1498
-
- Article
- Export citation
On a class of stable conditional measures
-
- Published online by Cambridge University Press:
- 01 November 2010, pp. 1499-1515
-
- Article
- Export citation
Diffeomorphisms with infinitely many irrational invariant curves
-
- Published online by Cambridge University Press:
- 23 November 2010, pp. 1517-1535
-
- Article
- Export citation
Newhouse phenomenon and homoclinic classes
-
- Published online by Cambridge University Press:
- 17 November 2010, pp. 1537-1562
-
- Article
- Export citation
Existence of a measurable saturated compensation function between subshifts and its applications
-
- Published online by Cambridge University Press:
- 13 September 2010, pp. 1563-1589
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 31 issue 5 Cover and Front matter
-
- Published online by Cambridge University Press:
- 05 September 2011, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
ETS volume 31 issue 5 Cover and Back matter
-
- Published online by Cambridge University Press:
- 05 September 2011, pp. b1-b8
-
- Article
-
- You have access
- Export citation


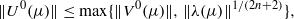
 and there exists a dense set 𝒟⊂𝒱 such that for all
and there exists a dense set 𝒟⊂𝒱 such that for all