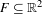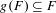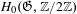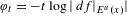Original Article
Self-embeddings of Bedford–McMullen carpets
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 577-603
-
- Article
- Export citation
Surjunctivity and topological rigidity of algebraic dynamical systems
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 604-619
-
- Article
- Export citation
A link between topological entropy and Lyapunov exponents
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 620-637
-
- Article
- Export citation
Badly approximable points on self-affine sponges and the lower Assouad dimension
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 638-657
-
- Article
-
- You have access
- Open access
- Export citation
Norm variation of ergodic averages with respect to two commuting transformations
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 658-688
-
- Article
- Export citation
Periodic approximation of Lyapunov exponents for Banach cocycles
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 689-706
-
- Article
- Export citation
Simple groups of dynamical origin
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 707-732
-
- Article
- Export citation
Dimensions of an overlapping generalization of Barański carpets
-
- Published online by Cambridge University Press:
- 25 September 2017, pp. 733-763
-
- Article
- Export citation
Thermodynamics of the Katok map
-
- Published online by Cambridge University Press:
- 28 June 2017, pp. 764-794
-
- Article
- Export citation
Purely exponential growth of cusp-uniform actions
-
- Published online by Cambridge University Press:
- 20 June 2017, pp. 795-831
-
- Article
- Export citation
Polynomial decay of correlations for almost Anosov diffeomorphisms
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 832-864
-
- Article
- Export citation
Front Cover (OFC, IFC) and matter
ETS volume 39 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
ETS volume 39 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 30 January 2019, pp. b1-b2
-
- Article
-
- You have access
- Export citation