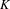Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T04:14:24.515Z Has data issue: false hasContentIssue false
  • English
  • Français

Wieler solenoids, Cuntz–Pimsner algebras and $K$-theory

Published online by Cambridge University Press:  02 May 2017

ROBIN J. DEELEY ,
MAGNUS GOFFENG ,
BRAM MESLAND  and
MICHAEL F. WHITTAKER
ROBIN J. DEELEY
Affiliation:
Department of Mathematics, University of Hawaii, 2565 McCarthy Mall, Keller 401A, Honolulu HI 96822, USA email [email protected]
MAGNUS GOFFENG
Affiliation:
Department of Mathematical Sciences, Chalmers University of Technology and The University of Gothenburg, SE-412 96 Gothenburg, Sweden email [email protected]
BRAM MESLAND
Affiliation:
Institut für Analysis, Leibniz Universität, Welfengarten 1, 30167 Hannover, Germany email [email protected]
MICHAEL F. WHITTAKER
Affiliation:
School of Mathematics and Statistics, University of Glasgow, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study irreducible Smale spaces with totally disconnected stable sets and their associated 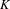$K$-theoretic invariants. Such Smale spaces arise as Wieler solenoids, and we restrict to those arising from open surjections. The paper follows three converging tracks: one dynamical, one operator algebraic and one 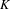$K$-theoretic. Using Wieler’s theorem, we characterize the unstable set of a finite set of periodic points as a locally trivial fibre bundle with discrete fibres over a compact space. This characterization gives us the tools to analyse an explicit groupoid Morita equivalence between the groupoids of Deaconu–Renault and Putnam–Spielberg, extending results of Thomsen. The Deaconu–Renault groupoid and the explicit Morita equivalence lead to a Cuntz–Pimsner model for the stable Ruelle algebra. The 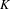$K$-theoretic invariants of Cuntz–Pimsner algebras are then studied using the Cuntz–Pimsner extension, for which we construct an unbounded representative. To elucidate the power of these constructions, we characterize the Kubo–Martin–Schwinger (KMS) weights on the stable Ruelle algebra of a Wieler solenoid. We conclude with several examples of Wieler solenoids, their associated algebras and spectral triples.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 8 , December 2018 , pp. 2942 - 2988
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Afsar, Z., an Huef, A. and Raeburn, I.. KMS states on C ∗ -algebras associated to local homeomorphisms. Internat. J. Math. 25 (2014), 28pp.Google Scholar
Agranovich, M. S.. Elliptic pseudodifferential operators on a closed curve. Tr. Mosk. Mat. Obs. 47 (1984), 22–67; 246.Google Scholar
Anderson, J. and Putnam, I. F.. Topological invariants for substitution tilings and their C ∗ -algebras. Ergod. Th. & Dynam. Sys. 18 (1998), 509–537.Google Scholar
Aoki, N. and Hiraide, K.. Topological Theory of Dynamical Systems (Recent Advances) (North-Holland Mathematical Library, 52) . North-Holland, Amsterdam, 1994.Google Scholar
Arici, F. and Rennie, A.. The Cuntz–Pimsner extension and mapping cone exact sequences. Preprint, 2016, arXiv:1605.08593.Google Scholar
Baaj, S. and Julg, P.. Théorie bivariante de Kasparov et operateurs non bornés dans les C ∗ -modules hilbertiens. C. R. Acad. Sci. Paris Sér. I Math. 296 (1983), 875–878.Google Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470) . Springer, New York, 1975.Google Scholar
Bratteli, O. and Robinson, D.. Operator Algebras and Quantum Statistical Mechanics, Vol. II (Texts and Monographs in Physics) . 2nd edn. Springer, New York, 2002.Google Scholar
Brownlowe, N., Buss, A., Gonçalves, D., Sims, A. and Whittaker, M. F.. $K$ -theoretic duality for self-similar group actions on graphs. In preparation.Google Scholar
Chen, X. and Hou, C.. Morita equivalence of groupoid C ∗ -algebras arising from dynamical systems. Studia Math. 149 (2002), 121–132.Google Scholar
Clark, A. and Hurder, S.. Homogeneous matchbox manifolds. Trans. Amer. Math. Soc. 365 (2013), 3151–3191.Google Scholar
Clark, A., Hurder, S. and Lukina, O.. The shape of matchbox manifolds. Indag. Math. (N.S.) 25 (2014), 669–712.Google Scholar
Connes, A.. Noncommutative Geometry. Academic Press, London, 1994.Google Scholar
Cuntz, J. and Krieger, W.. A class of C ∗ -algebras and topological Markov chains. Invent. Math. 56(3) (1980), 251–268.Google Scholar
Deaconu, V.. Generalized solenoids and C ∗ -algebras. Pacific J. Math. 190 (1999), 247–260.Google Scholar
Deeley, R. J., Killough, D. B. and Whittaker, M. F.. Dynamical correspondences for Smale spaces. New York J. Math. 22 (2016), 943–988.Google Scholar
Enomoto, M., Fujii, M. and Watatani, Y.. KMS states for the gauge action on O A . Math. Japan 29 (1984), 607–619.Google Scholar
Exel, R., an Huef, A. and Raeburn, I.. Purely infinite simple C ∗ -algebras associated to integer dilation matrices. Indiana Univ. Math. J. 60 (2011), 1033–1058.Google Scholar
Goffeng, M. and Mesland, B.. Spectral triples and finite summability on Cuntz–Krieger algebras. Doc. Math. 20 (2015), 89–170.Google Scholar
Goffeng, M., Mesland, B. and Rennie, A.. Shift–tail equivalence and an unbounded representative of the Cuntz–Pimsner extension. Ergod. Th. & Dynam. Sys., to appear, doi:10.1017/etds.2016.75, published online 8 November 2016.Google Scholar
Grubb, G.. The sectorial projection defined from logarithms. Math. Scand. 111 (2012), 118–126.Google Scholar
Kaminker, J., Putnam, I. F. and Whittaker, M. F.. $K$ -theoretic duality for hyperbolic dynamical systems. J. reine angew. Math., to appear, doi:10.1515/crelle-2014-0126, published online 2015, 1–37.Google Scholar
Kasparov, G. G.. The operator K-functor and extensions of C ∗ -algebras. Izv. Akad. Nauk SSSR Ser. Mat. 44 (1980), 571–636.Google Scholar
Kasparov, G. G.. Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91 (1988), 147–201.Google Scholar
Kucerovsky, D.. The KK-product of unbounded modules. K-Theory 11 (1997), 17–34.Google Scholar
Kumjian, A. and Renault, J.. KMS states on C ∗ -algebras associated to expansive maps. Proc. Amer. Math. Soc. 134 (2006), 2067–2078.Google Scholar
Laca, M. and Neshveyev, S.. KMS states of quasi-free dynamics on Pimsner algebras. J. Funct. Anal. 211 (2004), 457–482.Google Scholar
Laca, M., Raeburn, I., Ramagge, J. and Whittaker, M. F.. Equilibrium states on the Cuntz–Pimsner algebras of self-similar actions. J. Funct. Anal. 266 (2014), 6619–6661.Google Scholar
Lesch, M.. On the noncommutative residue for pseudodifferential operators with log-polyhomogeneous symbols. Ann. Global Anal. Geom. 17 (1999), 151–187.Google Scholar
Mesland, B.. Unbounded bivariant K-theory and correspondences in noncommutative geometry. J. Reine Angew. Math. 691 (2014), 101–172.Google Scholar
Mesland, B. and Rennie, A.. Nonunital spectral triples and metric completeness in unbounded KK-theory. J. Funct. Anal. 271 (2016), 2460–2538.Google Scholar
Muhly, P. S., Renault, J. and Williams, D. P.. Equivalence and isomorphism for groupoid C ∗ -algebras. J. Operator Theory 17 (1987), 3–22.Google Scholar
Nekrashevych, V.. Self-Similar Groups (Mathematical Surveys and Monographs, 117) . American Mathematical Society, Providence, RI, 2005.Google Scholar
Nekrashevych, V.. C ∗ -algebras and self-similar groups. J. Reine Angew. Math. 630 (2009), 59–123.Google Scholar
Olesen, D. and Pedersen, G. K.. Some C ∗ -dynamical systems with a single KMS state. Math. Scand. 42 (1978), 111–118.Google Scholar
Pavlov, A. A. and Troitskii, E. V.. Quantization of branched coverings. Russ. J. Math. Phys. 18 (2011), 338–352.Google Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple C ∗ -algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
Pimsner, M. V.. A class of C ∗ -algebras generalizing both Cuntz–Krieger algebras and crossed products by ℤ. Free Probability Theory (Waterloo, ON, 1995) (Fields Institute Communications, 12) . American Mathematical Society, Providence, RI, 1997, pp. 189–212.Google Scholar
Putnam, I. F.. C ∗ -algebras from Smale spaces. Canad. J. Math. 48 (1996), 175–195.Google Scholar
Putnam, I. F.. Lifting factor maps to resolving maps. Israel J. Math. 146 (2005), 253–280.Google Scholar
Putnam, I. F.. A Homology Theory for Smale Spaces (Memoirs of the American Mathematical Society, 232) . American Mathematical Society, Providence, RI, 2014.Google Scholar
Putnam, I. F.. Lecture Notes on Smale Spaces, Unpublished lecture notes, University of Victoria, http://www.math.uvic.ca/faculty/putnam/ln/Smale_spaces.pdf.Google Scholar
Putnam, I. F. and Spielberg, J.. The structure of C ∗ -algebras associated with hyperbolic dynamical systems. J. Funct. Anal. 163 (1999), 279–299.Google Scholar
Renault, J. N.. A Groupoid Approach to C ∗ -Algebras (Lecture Notes in Mathematics, 793) . Springer, Berlin, 1980.Google Scholar
Renault, J. N.. Cuntz-like Algebras (Operator Theoretical Methods) . Theta Foundation, Bucharest, 2000, pp. 371–386.Google Scholar
Rennie, A., Robertson, D. and Sims, A.. The extension class and KMS states for Cuntz–Pimsner algebras of some bi-Hilbertian bimodules. J. Topol. Anal., to appear, doi:10.1142/S1793525317500108, published online 2016, 1–31.Google Scholar
Ruelle, D.. Noncommutative algebras for hyperbolic diffeomorphisms. Invent. Math. 93 (1988), 1–13.Google Scholar
Ruelle, D.. Thermodynamic Formalism, 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Thomsen, K.. C ∗ -Algebras of Homoclinic and Heteroclinic Structure in Expansive Dynamics (Memoirs of the American Mathematical Society, 970) . American Mathematical Society, Providence, RI, 2010.Google Scholar
Thomsen, K.. On the C ∗ -algebra of a locally injective surjection and its KMS states. Comm. Math. Phys. 302 (2011), 403–423.Google Scholar
Walters, P.. Convergence of the Ruelle operator for a function satisfying Bowen’s condition. Trans. Amer. Math. Soc. 353 (2000), 327–347.Google Scholar
Wieler, S.. Smale spaces via inverse limits. Ergod. Th. & Dynam. Sys. 34 (2014), 2066–2092.Google Scholar
Williams, R. F.. Expanding attractors. Publ. Math. Inst. Hautes Études Sci. 43 (1974), 169–203.Google Scholar
Yi, I.. K-theory of C ∗ -algebras from one-dimensional generalized solenoids. J. Operator Theory 50 (2003), 283–295.Google Scholar