Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T21:22:37.815Z Has data issue: false hasContentIssue false
  • English
  • Français

Value distribution of derivatives in polynomial dynamics

Part of: Complex dynamical systems Holomorphic mappings and correspondences Arithmetic and non-Archimedean dynamical systems

Published online by Cambridge University Press:  05 January 2021

YÛSUKE OKUYAMA  and
GABRIEL VIGNY
YÛSUKE OKUYAMA
Affiliation:
Division of Mathematics, Kyoto Institute of Technology, Sakyo-ku, Kyoto606-8585, Japan (e-mail: [email protected])
GABRIEL VIGNY*
Affiliation:
LAMFA, UPJV, 33 rue Saint-Leu, 80039Amiens Cedex 1, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For every 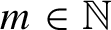$m\in \mathbb {N}$ , we establish the equidistribution of the sequence of the averaged pullbacks of a Dirac measure at any given value in 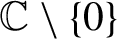$\mathbb {C}\setminus \{0\}$ under the 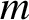$m$ th order derivatives of the iterates of a polynomials 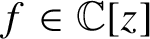$f\in \mathbb {C}[z]$ of degree $d>1$ towards the harmonic measure of the filled-in Julia set of f with pole at 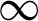$\infty $ . We also establish non-archimedean and arithmetic counterparts using the potential theory on the Berkovich projective line and the adelic equidistribution theory over a number field k for a sequence of effective divisors on 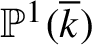$\mathbb {P}^1(\overline {k})$ having small diagonals and small heights. We show a similar result on the equidistribution of the analytic sets where the derivative of each iterate of a Hénon-type polynomial automorphism of $\mathbb {C}^2$ has a given eigenvalue.

Keywords

complex dynamicsHénon maphigher derivativenon-archimedean dynamicsvalue distribution

MSC classification

Primary: 37F10: Polynomials; rational maps; entire and meromorphic functions
Secondary: 37P30: Height functions; Green functions; invariant measures 32H50: Iteration problems
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 12 , December 2021 , pp. 3780 - 3806
Check for updates
Copyright
© The Author(s), 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Baker, M. H. and Hsia, L.-C.. Canonical heights, transfinite diameters, and polynomial dynamics. J. Reine Angew. Math. 585 (2005), 61–92.CrossRefGoogle Scholar
Baker, M. H. and Rumely, R.. Equidistribution of small points, rational dynamics, and potential theory. Ann. Inst. Fourier (Grenoble) 56(3) (2006), 625–688.CrossRefGoogle Scholar
Baker, M. H. and Rumely, R.. Potential Theory and Dynamics on the Berkovich Projective Line (Mathematical Surveys and Monographs, 159). American Mathematical Society, Providence, RI, 2010.CrossRefGoogle Scholar
Bedford, E. and Smillie, J.. Polynomial diffeomorphisms of ${\textbf{C}}^2$ . V. Critical points and Lyapunov exponents. J. Geom. Anal. 8(3) (1998), 349–383.CrossRefGoogle Scholar
Benedetto, R. L.. Dynamics in One Non-Archimedean Variable (Graduate Studies in Mathematics, 198). American Mathematical Society, Providence, RI, 2019.CrossRefGoogle Scholar
Berkovich, V. G.. Spectral Theory and Analytic Geometry over Non-Archimedean Fields (Mathematical Surveys and Monographs, 33). American Mathematical Society, Providence, RI, 1990.Google Scholar
Berteloot, F. and Mayer, V.. Rudiments de Dynamique Holomorphe (Cours Spécialisés, 7). Société Mathématique de France, Paris, 2001.Google Scholar
Brolin, H.. Invariant sets under iteration of rational functions. Ark. Mat. 6 (1965), 103–144.CrossRefGoogle Scholar
Chambert-Loir, A.. Mesures et équidistribution sur les espaces de Berkovich. J. Reine Angew. Math. 595 (2006), 215–235.Google Scholar
Dinh, T.-C. and Sibony, N.. Dynamics in several complex variables: endomorphisms of projective spaces and polynomial-like mappings. Holomorphic Dynamical Systems (Lecture Notes in Mathematics, 1998). Springer, Berlin, 2010, pp. 165–294.CrossRefGoogle Scholar
Dinh, T.-C. and Sibony, N.. Rigidity of Julia sets for Hénon type maps. J. Mod. Dyn. 8(3–4) (2014), 499–548.Google Scholar
Favre, C. and Jonsson, M.. The Valuative Tree (Lecture Notes in Mathematics, 1853). Springer, Berlin, 2004.CrossRefGoogle Scholar
Favre, C. and Rivera-Letelier, J.. Équidistribution quantitative des points de petite hauteur sur la droite projective. Math. Ann. 335(2) (2006), 311–361.10.1007/s00208-006-0751-xCrossRefGoogle Scholar
Favre, C. and Rivera-Letelier, J.. Théorie ergodique des fractions rationnelles sur un corps ultramétrique. Proc. Lond. Math. Soc. (3) 100(1) (2010), 116–154.CrossRefGoogle Scholar
Fornæss, J. E. and Sibony, N.. Complex dynamics in higher dimensions. Complex Potential Theory (Montreal, PQ, 1993) (NATO Advanced Science Institutes Series C: Mathematical and Physical Sciences, 439). Kluwer Academic Publishers, Dordrecht, 1994, pp. 131–186. Notes partially written by Estela A. Gavosto.CrossRefGoogle Scholar
Fresnel, J. and van der Put, M.. Rigid Analytic Geometry and its Applications (Progress in Mathematics, 218). Birkhäuser, Boston, 2004.CrossRefGoogle Scholar
Gauthier, T. and Vigny, G.. Distribution of points with prescribed derivative in polynomial dynamics. Riv. Math. Univ. Parma (N.S.) 8(2) (2017), 247–270.Google Scholar
Hörmander, L.. The Analysis of Linear Partial Differential Operators. I: Distribution Theory and Fourier Analysis (Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 256). Springer, Berlin, 1983.Google Scholar
Jonsson, M.. Dynamics on Berkovich spaces in low dimensions. Berkovich Spaces and Applications. Springer, Cham, 2015, pp. 205–366.Google Scholar
Milnor, J.. Dynamics in One Complex Variable (Annals of Mathematics Studies, 160), 3rd edn. Princeton University Press, Princeton, NJ, 2006.Google Scholar
Okuyama, Y.. Effective divisors on the projective line having small diagonals and small heights and their application to adelic dynamics. Pacific J. Math. 280(1) (2016), 141–175.CrossRefGoogle Scholar
Okuyama, Y.. Adelically summable normalized weights and adelic equidistribution of effective divisors having small diagonals and small heights on the Berkovich projective lines. Algebraic Number Theory and Related Topics 2014 (RIMS Kôkyûroku Bessatsu, B64). Research Institute for Mathematical Sciences (RIMS), Kyoto, 2017, pp. 55–66.Google Scholar
Okuyama, Y.. Value distribution of the sequences of the derivatives of iterated polynomials. Ann. Acad. Sci. Fenn. Math. 42(2) (2017), 563–574.CrossRefGoogle Scholar
Okuyama, Y.. An a priori bound of rational functions on the Berkovich projective line. Preprint, 2018, arXiv:1805.07668.Google Scholar
Ransford, T.. Potential Theory in the Complex Plane (London Mathematical Society Student Texts, 28). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Rivera-Letelier, J.. Dynamique des fonctions rationnelles sur des corps locaux. Geometric Methods in Dynamics. II (Astérisque, 287). Société Mathématique de France, Paris, 2003, pp. 147–230.Google Scholar
Russakovskii, A. and Shiffman, B.. Value distribution for sequences of rational mappings and complex dynamics. Indiana Univ. Math. J. 46(3) (1997), 897–932.CrossRefGoogle Scholar
Thuillier, A.. Théorie du potentiel sur les courbes en géométrie analytique non archimédienne. Applications à la théorie d’Arakelov. PhD Thesis, Université Rennes 1, 2005.Google Scholar
Yamanoi, K.. Zeros of higher derivatives of meromorphic functions in the complex plane. Proc. Lond. Math. Soc. (3) 106(4) (2013), 703–780.CrossRefGoogle Scholar
Ye, H.. The Schwarzian derivative and polynomial iteration. Conform. Geom. Dyn. 15 (2011), 113–132.CrossRefGoogle Scholar