Article contents
Uniformly perfect finitely generated simple left orderable groups
Published online by Cambridge University Press: 08 October 2019
Abstract
We show that the finitely generated simple left orderable groups 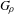 $G_{\!\unicode[STIX]{x1D70C}}$ constructed by the first two authors in Hyde and Lodha [Finitely generated infinite simple groups of homeomorphisms of the real line. Invent. Math. (2019), doi:10.1007/s00222-019-00880-7] are uniformly perfect—each element in the group can be expressed as a product of three commutators of elements in the group. This implies that the group does not admit any homogeneous quasimorphism. Moreover, any non-trivial action of the group on the circle, which lifts to an action on the real line, admits a global fixed point. It follows that any faithful action on the real line without a global fixed point is globally contracting. This answers Question 4 of the third author [A. Navas. Group actions on 1-manifolds: a list of very concrete open questions. Proceedings of the International Congress of Mathematicians, Vol. 2. Eds. B. Sirakov, P. Ney de Souza and M. Viana. World Scientific, Singapore, 2018, pp, 2029–2056], which asks whether such a group exists. This question has also been answered simultaneously and independently, using completely different methods, by Matte Bon and Triestino [Groups of piecewise linear homeomorphisms of flows. Preprint, 2018, arXiv:1811.12256]. To prove our results, we provide a characterization of elements of the group
$G_{\!\unicode[STIX]{x1D70C}}$ constructed by the first two authors in Hyde and Lodha [Finitely generated infinite simple groups of homeomorphisms of the real line. Invent. Math. (2019), doi:10.1007/s00222-019-00880-7] are uniformly perfect—each element in the group can be expressed as a product of three commutators of elements in the group. This implies that the group does not admit any homogeneous quasimorphism. Moreover, any non-trivial action of the group on the circle, which lifts to an action on the real line, admits a global fixed point. It follows that any faithful action on the real line without a global fixed point is globally contracting. This answers Question 4 of the third author [A. Navas. Group actions on 1-manifolds: a list of very concrete open questions. Proceedings of the International Congress of Mathematicians, Vol. 2. Eds. B. Sirakov, P. Ney de Souza and M. Viana. World Scientific, Singapore, 2018, pp, 2029–2056], which asks whether such a group exists. This question has also been answered simultaneously and independently, using completely different methods, by Matte Bon and Triestino [Groups of piecewise linear homeomorphisms of flows. Preprint, 2018, arXiv:1811.12256]. To prove our results, we provide a characterization of elements of the group 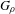 $G_{\!\unicode[STIX]{x1D70C}}$ which is a useful new tool in the study of these examples.
$G_{\!\unicode[STIX]{x1D70C}}$ which is a useful new tool in the study of these examples.
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2019
References
- 5
- Cited by



