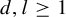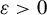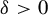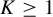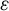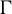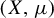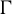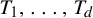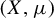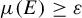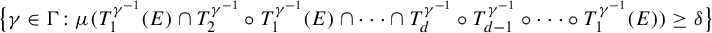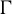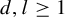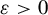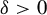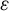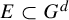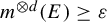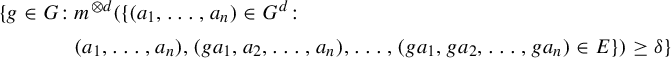1 Introduction
A subset of a group is called syndetic if the union of finitely many translates of it cover the whole group. Throughout, Følner nets are left Følner nets, and syndetic sets are left syndetic sets in non-commutative groups.
One version [Reference Furstenberg and Katznelson15] of Furstenburg’s multiple recurrence theorem [Reference Furstenberg14] is as follows.
Theorem 1.1. For every abelian group
![]() $\Gamma $
, each probability space
$\Gamma $
, each probability space
![]() $(X,\mu )$
with finitely many pairwise commuting measure-preserving
$(X,\mu )$
with finitely many pairwise commuting measure-preserving
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $T_i\curvearrowright (X,\mu )$
,
$T_i\curvearrowright (X,\mu )$
,
![]() $i=1,\ldots ,d$
, and all measurable sets E in X with positive measure, the return set
$i=1,\ldots ,d$
, and all measurable sets E in X with positive measure, the return set
is syndetic.
In this paper, our objective is to explore the uniformity of multiple recurrence theorems. There exist two directions of uniformity. First, can we establish a uniform lower bound for the measure of the multiple recurrence event, denoted as
![]() $\mu (E \cap T_1^\gamma (E) \cap T_2^\gamma (E) \cap \cdots \cap T_d^\gamma (E))$
, keeping it away from zero? Second, can we assert that the return set is uniformly not too small? Increasing the value of d or shrinking the measure of the set E might lead to a reduction in both the multiple recurrence event and the return set. Nevertheless, our aspiration is for these measures to remain independent of certain factors: the group
$\mu (E \cap T_1^\gamma (E) \cap T_2^\gamma (E) \cap \cdots \cap T_d^\gamma (E))$
, keeping it away from zero? Second, can we assert that the return set is uniformly not too small? Increasing the value of d or shrinking the measure of the set E might lead to a reduction in both the multiple recurrence event and the return set. Nevertheless, our aspiration is for these measures to remain independent of certain factors: the group
![]() $\Gamma $
, the probability space
$\Gamma $
, the probability space
![]() $(X, \mu )$
, the commuting measure-preserving
$(X, \mu )$
, the commuting measure-preserving
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $T_1,\ldots ,T_d$
, and the choice of measurable set E—as long as we fixed d and
$T_1,\ldots ,T_d$
, and the choice of measurable set E—as long as we fixed d and
![]() $\mu (E)$
.
$\mu (E)$
.
To pursue the second aspect of uniformity, it becomes necessary to establish a method for quantifying the size of a subset within a group. In light of the statement of Theorem 1.1, a natural choice is to use the concept of K-syndeticity: given a group
![]() $\Gamma $
and an integer
$\Gamma $
and an integer
![]() $K\geq 1$
, a subset
$K\geq 1$
, a subset
![]() $S\subset \Gamma $
is said to be K-syndetic if K many translates of S cover
$S\subset \Gamma $
is said to be K-syndetic if K many translates of S cover
![]() $\Gamma $
. (In a previous version of this paper, we quantified syndeticity using the size of the lower Banach density of a subset. We are indebted to the anonymous referee for suggesting the use of the more natural (and seemingly stronger) concept of K-syndicity, which also had the benefit of significantly simplifying the proof of our main uniform syndeticity result.)
$\Gamma $
. (In a previous version of this paper, we quantified syndeticity using the size of the lower Banach density of a subset. We are indebted to the anonymous referee for suggesting the use of the more natural (and seemingly stronger) concept of K-syndicity, which also had the benefit of significantly simplifying the proof of our main uniform syndeticity result.)
Numerous findings pertaining to uniform syndeticity are available within the existing literature. Among these, a notable contribution was made by Furstenberg and Katznelson, who demonstrated the prevalence of uniform syndeticity across all
![]() $\mathbb {Z}$
-actions.
$\mathbb {Z}$
-actions.
Theorem 1.2. (Uniform syndeticity,
 $\mathbb {Z}$
-case)
$\mathbb {Z}$
-case)
For every integer
![]() $d\geq 1$
and any
$d\geq 1$
and any
![]() $\varepsilon>0$
, there are
$\varepsilon>0$
, there are
![]() $\delta>0$
and
$\delta>0$
and
![]() $K\geq 1$
(only depending on
$K\geq 1$
(only depending on
![]() $\varepsilon ,d$
) such that for any probability space
$\varepsilon ,d$
) such that for any probability space
![]() $(X,\mu )$
, every d many pairwise commuting measure-preserving transformations
$(X,\mu )$
, every d many pairwise commuting measure-preserving transformations
![]() $T_i\colon X\to X$
,
$T_i\colon X\to X$
,
![]() $i=1,\ldots ,d$
, and all measurable sets E in X with
$i=1,\ldots ,d$
, and all measurable sets E in X with
![]() $\mu (E)\geq \varepsilon $
, it holds that
$\mu (E)\geq \varepsilon $
, it holds that
is K-syndetic.
Proof. This result can be deduced from [Reference Bergelson, Host, McCutcheon and Parreau5, Theorem 2.1(iii)].
The following weaker assertion is established for a fixed arbitrary countable abelian group by Furstenberg and Katznelson in their work [Reference Furstenberg and Katznelson15]. In this version of uniform syndeticity, the probability of the multiple recurrence event is not shown to be uniformly bounded away from zero, as observed in Theorem 1.2 or later shown in Theorem 1.5.
Theorem 1.3. (Weak uniform syndeticity, countable abelian case)
Let
![]() $\Gamma $
be a countable abelian group. For every integer
$\Gamma $
be a countable abelian group. For every integer
![]() $d\geq 1$
and any
$d\geq 1$
and any
![]() $\varepsilon>0$
, there exists
$\varepsilon>0$
, there exists
![]() $K\geq 1$
(only depending on
$K\geq 1$
(only depending on
![]() $\varepsilon ,d$
, and
$\varepsilon ,d$
, and
![]() $\Gamma $
) such that for any probability space
$\Gamma $
) such that for any probability space
![]() $(X,\mu )$
, every d many pairwise commuting measure-preserving actions
$(X,\mu )$
, every d many pairwise commuting measure-preserving actions
![]() $T_i\colon \Gamma \curvearrowright (X,\mu )$
,
$T_i\colon \Gamma \curvearrowright (X,\mu )$
,
![]() $i=1,\ldots ,d$
, and every measurable set E in X with
$i=1,\ldots ,d$
, and every measurable set E in X with
![]() $\mu (E)\geq \varepsilon $
, it holds that
$\mu (E)\geq \varepsilon $
, it holds that
is K-syndetic.
Proof. The claim follows from combining the results in [Reference Furstenberg and Katznelson15, §10], see the last remark therein.
Remark 1.4. In fact, in [Reference Furstenberg and Katznelson15], Furstenberg and Katznelson establish that the return set
satisfies stronger notions of largeness than syndeticity such as IP
![]() $^{*}$
or even IP
$^{*}$
or even IP
![]() $^{*}_r$
. However, we will focus on strengthening and generalizing the slightly weaker consequence stated in Theorem 1.3.
$^{*}_r$
. However, we will focus on strengthening and generalizing the slightly weaker consequence stated in Theorem 1.3.
Our main result establishes a new proof and a joint generalization and strengthening of Theorems 1.2 and 1.3 by relaxing the dependence of
![]() $\delta $
and K on the acting group.
$\delta $
and K on the acting group.
Theorem 1.5. For all integers
![]() $d,l\geq 1$
and any
$d,l\geq 1$
and any
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $K\geq 1$
(only depending on
$K\geq 1$
(only depending on
![]() $\varepsilon ,d,l$
) such that for any solvable group
$\varepsilon ,d,l$
) such that for any solvable group
![]() $\Gamma $
of derived length l, any probability space
$\Gamma $
of derived length l, any probability space
![]() $(X,\mu )$
, every d many pairwise commuting measure-preserving actions
$(X,\mu )$
, every d many pairwise commuting measure-preserving actions
![]() $T_i\colon \Gamma \curvearrowright (X,\mu )$
,
$T_i\colon \Gamma \curvearrowright (X,\mu )$
,
![]() $i=1,\ldots ,d$
, and every measurable set E in X with
$i=1,\ldots ,d$
, and every measurable set E in X with
![]() $\mu (E)\geq \varepsilon $
, it holds that
$\mu (E)\geq \varepsilon $
, it holds that
is K-syndetic, where
![]() $T_{[a,b]}^{\gamma }:=T_{a}^{\gamma }\circ T_{a+1}^{\gamma }\circ \cdots \circ T_{b}^{\gamma }$
.
$T_{[a,b]}^{\gamma }:=T_{a}^{\gamma }\circ T_{a+1}^{\gamma }\circ \cdots \circ T_{b}^{\gamma }$
.
We recall that the derived length n of a solvable group
![]() $\Gamma $
is the least n for which
$\Gamma $
is the least n for which
![]() $\Gamma ^{(n)}=1$
, where
$\Gamma ^{(n)}=1$
, where
![]() $\Gamma ^{(i)}$
is recursively defined by
$\Gamma ^{(i)}$
is recursively defined by
![]() $\Gamma ^{(0)}=\Gamma $
and
$\Gamma ^{(0)}=\Gamma $
and
![]() $\Gamma ^{(i+1)}$
is the commutator subgroup
$\Gamma ^{(i+1)}$
is the commutator subgroup
![]() $[\Gamma ^{(i)},\Gamma ^{(i)}]$
of
$[\Gamma ^{(i)},\Gamma ^{(i)}]$
of
![]() $\Gamma ^{(i)}$
.
$\Gamma ^{(i)}$
.
Remark 1.6. In fact, we establish a more general version of Theorem 1.5 where we can consider any uniformly amenable class of groups, of which a class of solvable groups of fixed derived length is an example. See §2 for the definition of uniform amenability and Theorem 3.2 for the general statement.
Remark 1.7. It is important to discern the variance in the articulation of the multiple recurrence event in the abelian case in Theorems 1.1, 1.2, and 1.3, where we consider
![]() $T_i^\gamma $
rather than the composite actions
$T_i^\gamma $
rather than the composite actions
![]() $T_{[1,i]}^{\gamma }$
as presented in the formulation of Theorem 1.5. The possibility of attaining an analogous formulation to Theorems 1.1, 1.2, and 1.3 does indeed arise for nilpotent groups. However, it is crucial to note, as observed by Bergelson and Leibman in [Reference Bergelson and Leibman6], that such a formulation fails to hold universally for solvable groups.
$T_{[1,i]}^{\gamma }$
as presented in the formulation of Theorem 1.5. The possibility of attaining an analogous formulation to Theorems 1.1, 1.2, and 1.3 does indeed arise for nilpotent groups. However, it is crucial to note, as observed by Bergelson and Leibman in [Reference Bergelson and Leibman6], that such a formulation fails to hold universally for solvable groups.
Remark 1.8. Quantitatively stronger results in the form of Khintchine-type bounds are available in more specific situations, as seen in [Reference Ackelsberg, Bergelson and Shalom1, Reference Bergelson, Host and Kra4, Reference Bergelson, Tao and Ziegler10–Reference Chu and Zorin-Kranich12, Reference Shalom22]. To the best of our knowledge, Theorem 1.5 is the first result of its kind to establish the existence of uniform bounds for arbitrary d, independent of
![]() $\Gamma $
(within a large class of groups), and without requiring the hypothesis of ergodicity.
$\Gamma $
(within a large class of groups), and without requiring the hypothesis of ergodicity.
Remark 1.9. In [Reference Durcik, Greenfeld, Iseli, Jamneshan and Madrid13], the first author and coauthors established a slightly weaker formulation of Theorem 1.5 (in fact, of the general Theorem 3.2) for two commuting actions involving, instead of K-syndeticity, a uniformly lower bound on the lower Banach density of the return set. The proof in [Reference Durcik, Greenfeld, Iseli, Jamneshan and Madrid13] relied on certain technical lemmas about the interplay of Hahn–Banach type extensions for finitely additive invariant means and ultralimits of lower Banach densities. Using the stronger K-syndeticity formulation, our proof not only establishes a stronger generalization of the result in [Reference Durcik, Greenfeld, Iseli, Jamneshan and Madrid13] to finitely many commuting actions, but also significantly simplifies (in particular, no Hahn–Banach type theorems and ultralimits of lower Banach densities are required anymore) and basically follows from an ultralimit construction of Austin’s amenable ergodic Szemerédi theorem as stated next.
A pivotal step in demonstrating Theorem 1.5 hinges on employing ultraproducts of measure-preserving dynamical systems. However, the resultant ultraproduct groups are often not countable and the corresponding Loeb probability spaces lack separability. Addressing these challenges introduces certain measure-theoretic subtleties, discussed comprehensively in [Reference Jamneshan and Tao20]. To navigate around these intricacies, an abstract category of probability algebra dynamical systems
![]() $\mathbf {PrbAlg}_\Gamma $
has been identified (see [Reference Jamneshan18–Reference Jamneshan and Tao21]). The abstract system is obtained from a concrete probability space by abstracting away the intrinsic point structure and exclusively focusing on the relationships between measurable sets, considering operations such as intersections, unions, and complementations.
$\mathbf {PrbAlg}_\Gamma $
has been identified (see [Reference Jamneshan18–Reference Jamneshan and Tao21]). The abstract system is obtained from a concrete probability space by abstracting away the intrinsic point structure and exclusively focusing on the relationships between measurable sets, considering operations such as intersections, unions, and complementations.
![]() $\mathbf {PrbAlg}_\Gamma $
, along with the tools to work with its objects, is gathered in §2.1
$\mathbf {PrbAlg}_\Gamma $
, along with the tools to work with its objects, is gathered in §2.1
Equipped with these tools in the domain of uncountable ergodic theory, we extend Austin’s amenable multiple recurrence theorem [Reference Austin2] to encompass the actions of uncountable amenable groups on inseparable probability spaces in the following theorem. This uncountable variant of Austin’s theorem is then applied to the ultraproduct systems, playing a key role in proving Theorem 1.5.
Theorem 1.10. Let
![]() $\Gamma $
be an arbitrary discrete amenable group and let
$\Gamma $
be an arbitrary discrete amenable group and let
![]() $(X,\mu ,T)$
be a
$(X,\mu ,T)$
be a
![]() $\mathbf {PrbAlg}_{\Gamma ^d}$
-system, that is, there are finitely many commuting measure-preserving
$\mathbf {PrbAlg}_{\Gamma ^d}$
-system, that is, there are finitely many commuting measure-preserving
![]() $\Gamma $
-actions
$\Gamma $
-actions
![]() $T_i\colon \Gamma \curvearrowright (X,\mu )$
,
$T_i\colon \Gamma \curvearrowright (X,\mu )$
,
![]() $i=1,\ldots ,d$
, where
$i=1,\ldots ,d$
, where
![]() $(X,\mu )$
is a probability algebra. Let
$(X,\mu )$
is a probability algebra. Let
![]() $f_{1},\ldots ,f_{d}\in L^{\infty }(X,\mu )$
and let
$f_{1},\ldots ,f_{d}\in L^{\infty }(X,\mu )$
and let
![]() $(\Phi _{\kappa })$
be a Følner net for
$(\Phi _{\kappa })$
be a Følner net for
![]() $\Gamma $
. Then the limit
$\Gamma $
. Then the limit
 $$ \begin{align} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\prod_{i=1}^{d}f_i\circ {T_{[1,i]}^{\gamma}} \end{align} $$
$$ \begin{align} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\prod_{i=1}^{d}f_i\circ {T_{[1,i]}^{\gamma}} \end{align} $$
exists in
![]() $L^{2}(X,\mu )$
and is independent of the Følner net. Moreover, if a measurable set E in X is such that
$L^{2}(X,\mu )$
and is independent of the Følner net. Moreover, if a measurable set E in X is such that
![]() $\mu (E)>0$
, then
$\mu (E)>0$
, then
 $$ \begin{align} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\mu \bigg( \bigcap_{i=0}^{d}T_{[1,i]}^{\gamma^{-1}}(E)\bigg)>0. \end{align} $$
$$ \begin{align} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\mu \bigg( \bigcap_{i=0}^{d}T_{[1,i]}^{\gamma^{-1}}(E)\bigg)>0. \end{align} $$
In particular, there exists
![]() $\varepsilon>0$
such that
$\varepsilon>0$
such that
 $$ \begin{align} \bigg\{ \gamma \in \Gamma \colon \mu \bigg( \bigcap_{i=0}^{d}T_{[1,i]}^{\gamma^{-1}}(E)\bigg)>\varepsilon \bigg\} \end{align} $$
$$ \begin{align} \bigg\{ \gamma \in \Gamma \colon \mu \bigg( \bigcap_{i=0}^{d}T_{[1,i]}^{\gamma^{-1}}(E)\bigg)>\varepsilon \bigg\} \end{align} $$
is syndetic in
![]() $\Gamma $
.
$\Gamma $
.
The case of two commuting transformations of Theorem 1.10 was previously established in [Reference Durcik, Greenfeld, Iseli, Jamneshan and Madrid13] by the first author and coauthors. They generalized the proof of the amenable double recurrence theorem by Bergelson, McCutcheon, and Zhang from [Reference Bergelson, McCutcheon and Zhang8]. Zorin-Kranich [Reference Zorin-Kranich26] establishes the limit claim in equation (1) of Theorem 1.10 in full generality using an adaptation of functional analytic methods developed by Walsh [Reference Walsh24], who established the
![]() $L^2$
-limit in the case of finitely many actions of a nilpotent group. However, Zorin-Kranich’s result does not provide information about the limit; in particular, it does not yield the multiple recurrence statements in equations (2) and (3). These multiple recurrence statements are established in the case of countable amenable groups by Austin [Reference Austin2] using sated extensions. Our proof of Theorem 1.10 will modify necessary steps in [Reference Austin2] to tailor his proof to our uncountable setting.
$L^2$
-limit in the case of finitely many actions of a nilpotent group. However, Zorin-Kranich’s result does not provide information about the limit; in particular, it does not yield the multiple recurrence statements in equations (2) and (3). These multiple recurrence statements are established in the case of countable amenable groups by Austin [Reference Austin2] using sated extensions. Our proof of Theorem 1.10 will modify necessary steps in [Reference Austin2] to tailor his proof to our uncountable setting.
1.1 Combinatorial application
As an immediate consequence of Theorem 1.5, we obtain the following combinatorial application. For a finite group G, we denote by m the uniform measure. On
![]() $G^d$
, we denote by
$G^d$
, we denote by
![]() $m^{\otimes d}$
the d-fold product of the uniform measure.
$m^{\otimes d}$
the d-fold product of the uniform measure.
Corollary 1.11. Let
![]() $d,l{\kern-1pt}\geq{\kern-1pt} 1$
be integers and let
$d,l{\kern-1pt}\geq{\kern-1pt} 1$
be integers and let
![]() $\varepsilon{\kern-1pt}>{\kern-1pt} 0$
. Then there are
$\varepsilon{\kern-1pt}>{\kern-1pt} 0$
. Then there are
![]() ${\delta {\kern-1pt}={\kern-1pt}\delta (d,l,\varepsilon ){\kern-1pt}>{\kern-1pt}0}$
and
${\delta {\kern-1pt}={\kern-1pt}\delta (d,l,\varepsilon ){\kern-1pt}>{\kern-1pt}0}$
and
![]() $K=K(d,l,\varepsilon )\geq 1$
such that for all finite solvable groups G of derived length l and any subset
$K=K(d,l,\varepsilon )\geq 1$
such that for all finite solvable groups G of derived length l and any subset
![]() $E\subset G^d$
with
$E\subset G^d$
with
![]() $m^{\otimes d}(E)\geq \varepsilon $
, we have that
$m^{\otimes d}(E)\geq \varepsilon $
, we have that
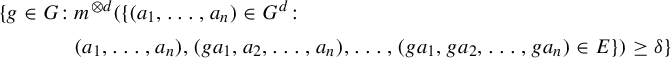 $$ \begin{align*} \{g\in G\colon &m^{\otimes d}(\{(a_1,\ldots,a_n)\in G^d\colon \\ & (a_1,\ldots,a_n),(ga_1,a_2,\ldots,a_n),\ldots,(ga_1,ga_2,\ldots, ga_n)\in E\})\geq \delta \} \end{align*} $$
$$ \begin{align*} \{g\in G\colon &m^{\otimes d}(\{(a_1,\ldots,a_n)\in G^d\colon \\ & (a_1,\ldots,a_n),(ga_1,a_2,\ldots,a_n),\ldots,(ga_1,ga_2,\ldots, ga_n)\in E\})\geq \delta \} \end{align*} $$
is K-syndetic.
Remark 1.12. In [Reference Bergelson, Robertson and Zorin-Kranich9, Theorem 1.5], the authors establish K-syndeticity for the density of triangle configurations with a Khintchine-type lower bound in a fixed class of quasirandom ultraproduct groups. In [Reference Bergelson, Robertson and Zorin-Kranich9, Corollary 1.6], they deduce a similar consequence for the class of all non-cyclic finite simple groups. Their proof relies on a convergence theorem along minimal idempotent ultrafilters for ergodic averages formed by two commuting actions of a minimally almost periodic group.
1.2 Discussion
In Theorem 3.2, we prove a more general version of Theorem 1.5, establishing a strong form of uniform syndeticity within any uniformly amenable class of groups. We then derive Theorem 1.5 by demonstrating that the class of solvable groups with a fixed derived length is uniformly amenable. A key property in this verification is that the class of solvable groups with a fixed derived length is closed under countable direct products.
Since Theorem 1.10 holds for all amenable groups, a natural question arises: does Theorem 1.5 remain valid for the entire class of amenable groups (that is,
![]() $K,\delta $
only depend on
$K,\delta $
only depend on
![]() $\varepsilon , d$
and are uniform for all amenable acting groups)? The methods employed in this paper cannot address this question. Indeed, the countable direct product of arbitrary nilpotent groups is not amenable in general, which essentially undermines our strategy based on Theorem 1.10 to prove uniform syndeticity. We are grateful to Dave Benson for this observation. Additionally, an example of an amenable group that is not uniformly amenable is given in [Reference Wysoczański25].
$\varepsilon , d$
and are uniform for all amenable acting groups)? The methods employed in this paper cannot address this question. Indeed, the countable direct product of arbitrary nilpotent groups is not amenable in general, which essentially undermines our strategy based on Theorem 1.10 to prove uniform syndeticity. We are grateful to Dave Benson for this observation. Additionally, an example of an amenable group that is not uniformly amenable is given in [Reference Wysoczański25].
However, the results of [Reference Bergelson and McCutcheon7] give hope that Theorem 1.10 holds for all amenable groups (or even for the class of all groups). In [Reference Bergelson and McCutcheon7, Theorem 1.3], the authors establish the consequence in equation (3) of Theorem 1.10 for the action of an arbitrary countable group in the case of two commuting actions. (Actually, they establish the stronger conclusion that the return set is
![]() $\mathcal {C}^{*}$
, we refer the interested reader to [Reference Bergelson and McCutcheon7] for the definition of a central
$\mathcal {C}^{*}$
, we refer the interested reader to [Reference Bergelson and McCutcheon7] for the definition of a central
![]() $^{*}$
subset of a group.) Proving an uncountable version of [Reference Bergelson and McCutcheon7, Theorem 1.3] should, in principle, yield the analogue of Theorem 1.5 for the class of all groups in the case of two commuting actions by the same proof as given in §3. To our knowledge, the analogue of [Reference Bergelson and McCutcheon7, Theorem 1.3] in the case of more than two commuting actions of an arbitrary countable group is unknown. A potential line of attack, suggested by Austin [Reference Austin2], is to combine the technique of stated extensions and the ultrafilter techniques in [Reference Bergelson and McCutcheon7]. We hope to address these questions in future work.
$^{*}$
subset of a group.) Proving an uncountable version of [Reference Bergelson and McCutcheon7, Theorem 1.3] should, in principle, yield the analogue of Theorem 1.5 for the class of all groups in the case of two commuting actions by the same proof as given in §3. To our knowledge, the analogue of [Reference Bergelson and McCutcheon7, Theorem 1.3] in the case of more than two commuting actions of an arbitrary countable group is unknown. A potential line of attack, suggested by Austin [Reference Austin2], is to combine the technique of stated extensions and the ultrafilter techniques in [Reference Bergelson and McCutcheon7]. We hope to address these questions in future work.
2 Tools
2.1 The category of probability algebra dynamical systems
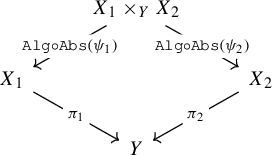
We now formalize the ‘point-free’ approach by introducing the category of probability algebra dynamical systems and the canonical model functor, see Figure 1. For a comprehensive background, references, and any unexplained concepts which are used in the following, we refer the interested reader to [Reference Jamneshan and Tao20].
Definition 2.1. (Categories and functors)
-
(i) We denote by
 ${\mathbf {CHPrb}}$
the category of compact Hausdorff spaces equipped with a Baire–Radon probability measure and measure-preserving continuous functions.
${\mathbf {CHPrb}}$
the category of compact Hausdorff spaces equipped with a Baire–Radon probability measure and measure-preserving continuous functions. -
(ii) We denote by
 $\mathbf {AbsMbl}$
the category of abstract measurable spaces which we define as the opposite category of the category of
$\mathbf {AbsMbl}$
the category of abstract measurable spaces which we define as the opposite category of the category of
 $\sigma $
-complete Boolean algebras and
$\sigma $
-complete Boolean algebras and
 $\sigma $
-complete Boolean homomorphisms.
$\sigma $
-complete Boolean homomorphisms. -
(iii) We denote by
 $\mathbf {PrbAlg}$
the opposite category of the category of probability algebras and measure-preserving Boolean homomorphisms. Note that the category
$\mathbf {PrbAlg}$
the opposite category of the category of probability algebras and measure-preserving Boolean homomorphisms. Note that the category
 $\mathbf {PrbAlg}$
has arbitrary inverse limits (e.g., see [Reference Jamneshan and Tao20]), a fact which will be useful for us later.
$\mathbf {PrbAlg}$
has arbitrary inverse limits (e.g., see [Reference Jamneshan and Tao20]), a fact which will be useful for us later. -
(iv) We denote by
 $\mathbf {Hilb}$
the category of complex Hilbert spaces and linear isometries.
$\mathbf {Hilb}$
the category of complex Hilbert spaces and linear isometries. -
(v) Given a (discrete) group
 $\Gamma $
, we can turn a category
$\Gamma $
, we can turn a category
 $ \mathcal {C}=\mathbf {Hilb}, \mathbf {PrbAlg}, {\mathbf {CHPrb}} $
into a dynamical category
$ \mathcal {C}=\mathbf {Hilb}, \mathbf {PrbAlg}, {\mathbf {CHPrb}} $
into a dynamical category
 $\mathcal {C}_\Gamma $
as follows. Given an object X in
$\mathcal {C}_\Gamma $
as follows. Given an object X in
 $ \mathcal {C}$
, we can associate with X the group
$ \mathcal {C}$
, we can associate with X the group
 $\mathrm {Aut}(X)$
of its automorphisms in
$\mathrm {Aut}(X)$
of its automorphisms in
 $\mathcal {C}$
. The dynamical category
$\mathcal {C}$
. The dynamical category
 $\mathcal {C}_\Gamma $
now consists of pairs
$\mathcal {C}_\Gamma $
now consists of pairs
 $(X,T)$
, where X is a
$(X,T)$
, where X is a
 $\mathcal {C}$
-object and
$\mathcal {C}$
-object and
 $ T\colon \Gamma \to \mathrm {Aut}(X)$
a group homomorphism. A
$ T\colon \Gamma \to \mathrm {Aut}(X)$
a group homomorphism. A
 $\mathcal {C}_\Gamma $
-morphism is a
$\mathcal {C}_\Gamma $
-morphism is a
 $\mathcal {C}$
-morphism which intertwines with the
$\mathcal {C}$
-morphism which intertwines with the
 $\Gamma $
-actions.
$\Gamma $
-actions. -
(vi) The abstraction functor
 $\texttt {Abs}$
maps a concrete measurable space
$\texttt {Abs}$
maps a concrete measurable space
 $(X,\Sigma _X)$
to the
$(X,\Sigma _X)$
to the
 $\mathbf {AbsMbl}$
-object
$\mathbf {AbsMbl}$
-object
 $\Sigma _X$
and a measurable function
$\Sigma _X$
and a measurable function
 $f:(X,\Sigma _X)\to (Y,\Sigma _Y)$
to the
$f:(X,\Sigma _X)\to (Y,\Sigma _Y)$
to the
 $\mathbf {AbsMbl}$
-morphism
$\mathbf {AbsMbl}$
-morphism
 $f^{*}:\Sigma _X\to \Sigma _Y$
, where
$f^{*}:\Sigma _X\to \Sigma _Y$
, where
 $f^{*}$
is the (opposite) pullback map
$f^{*}$
is the (opposite) pullback map
 $f^{*}(E):=f^{-1}(E)$
,
$f^{*}(E):=f^{-1}(E)$
,
 $E\in \Sigma _Y$
. We apply the
$E\in \Sigma _Y$
. We apply the
 $\texttt {Abs} $
-functor to a concrete probability space
$\texttt {Abs} $
-functor to a concrete probability space
 $(X,\Sigma _X,\mu )$
and obtain an abstract probability space
$(X,\Sigma _X,\mu )$
and obtain an abstract probability space
 $(\Sigma _X,\mu )$
. Let
$(\Sigma _X,\mu )$
. Let
 $\mathcal {I}_\mu =\{E\in \Sigma _X: \mu (E)=0\}$
be the ideal of
$\mathcal {I}_\mu =\{E\in \Sigma _X: \mu (E)=0\}$
be the ideal of
 $\mu $
-null sets. Then the quotient Boolean algebra
$\mu $
-null sets. Then the quotient Boolean algebra  is
is
 $\sigma $
-complete. We can lift the measure
$\sigma $
-complete. We can lift the measure
 $\mu $
to
$\mu $
to
 $X_\mu $
in a natural way and, by an abuse of notation, we denote this lift by
$X_\mu $
in a natural way and, by an abuse of notation, we denote this lift by
 $\mu $
again. The tuple
$\mu $
again. The tuple
 $ (X_\mu ,\mu )$
is a probability algebra and we define
$ (X_\mu ,\mu )$
is a probability algebra and we define
 $\texttt {Alg}\circ \texttt {Abs}(X,\Sigma _X,\mu _X):=(X_\mu ,\mu )$
. If
$\texttt {Alg}\circ \texttt {Abs}(X,\Sigma _X,\mu _X):=(X_\mu ,\mu )$
. If
 $f\colon (X,\Sigma _X,\mu )\to (Y,\Sigma _Y,\nu )$
is a measure-preserving function, then the pullback map
$f\colon (X,\Sigma _X,\mu )\to (Y,\Sigma _Y,\nu )$
is a measure-preserving function, then the pullback map
 $f^{*}$
maps the ideal
$f^{*}$
maps the ideal
 $\mathcal {I}_\nu $
to the ideal
$\mathcal {I}_\nu $
to the ideal
 $ \mathcal {I}_\mu $
. We obtain a
$ \mathcal {I}_\mu $
. We obtain a
 $\mathbf {PrbAlg}$
-morphism
$\mathbf {PrbAlg}$
-morphism
 $\texttt {Alg}\circ \texttt {Abs}(f)\colon (X_\mu ,\mu )\to (Y_\nu ,\nu )$
.
$\texttt {Alg}\circ \texttt {Abs}(f)\colon (X_\mu ,\mu )\to (Y_\nu ,\nu )$
. -
(vii) The canonical model functor
 $\texttt {Conc}$
reverses the process described in the previous item. More precisely, if
$\texttt {Conc}$
reverses the process described in the previous item. More precisely, if
 $(X,\mu )$
is a probability algebra, there exists a
$(X,\mu )$
is a probability algebra, there exists a
 ${\mathbf {CHPrb}}$
-space
${\mathbf {CHPrb}}$
-space  such that
such that
 $\texttt {Alg}\circ \texttt {Abs}(Z,\mathcal {B}a(Z),\mu _{Z})$
is isomorphic to
$\texttt {Alg}\circ \texttt {Abs}(Z,\mathcal {B}a(Z),\mu _{Z})$
is isomorphic to
 $(X,\mu )$
in
$(X,\mu )$
in
 $ \mathbf {PrbAlg}$
. A complete construction of
$ \mathbf {PrbAlg}$
. A complete construction of
 $\texttt {Conc} (X,\mu )$
can be found in [Reference Jamneshan and Tao20]. Given a
$\texttt {Conc} (X,\mu )$
can be found in [Reference Jamneshan and Tao20]. Given a
 $\mathbf {PrbAlg}$
-morphism
$\mathbf {PrbAlg}$
-morphism
 $f:(X,\mu )\rightarrow (Y,\nu )$
, we define
$f:(X,\mu )\rightarrow (Y,\nu )$
, we define
 ${\texttt {Conc}(f):Z_{X}\rightarrow Z_{Y}}$
by
${\texttt {Conc}(f):Z_{X}\rightarrow Z_{Y}}$
by
 $\texttt{Conc}(f)(\theta )=\theta \circ \phi $
.
$\texttt{Conc}(f)(\theta )=\theta \circ \phi $
. -
(viii) Next we define the
 $L^{2}$
-functor. Let
$L^{2}$
-functor. Let
 $(X,\mu )$
be a
$(X,\mu )$
be a
 $ \mathbf {PrbAlg}$
-space with canonical model
$ \mathbf {PrbAlg}$
-space with canonical model
 $\texttt {Conc}(X,\mu )=(Z, \mathcal {B}a(Z),\mu _{Z})$
, as constructed previously. We define the
$\texttt {Conc}(X,\mu )=(Z, \mathcal {B}a(Z),\mu _{Z})$
, as constructed previously. We define the
 $L^{2}$
-functor on objects by
$L^{2}$
-functor on objects by  . If
. If
 $\pi :(X,\mu )\rightarrow (Y,\nu )$
is a
$\pi :(X,\mu )\rightarrow (Y,\nu )$
is a
 $\mathbf {PrbAlg}$
-morphism, then
$\mathbf {PrbAlg}$
-morphism, then
 $L^{2}(\pi ):L^{2}(Y,\nu )\rightarrow L^{2}(X,\mu )$
is defined by the Koopman operator
$L^{2}(\pi ):L^{2}(Y,\nu )\rightarrow L^{2}(X,\mu )$
is defined by the Koopman operator  , where
, where  .
. -
(ix) Similarly, we define the dynamical version of the functors
 $ \texttt {Abs}\circ \texttt {Alg}$
,
$ \texttt {Abs}\circ \texttt {Alg}$
,
 $\texttt {Conc}$
, and
$\texttt {Conc}$
, and
 $L^{2}$
.
$L^{2}$
.

Figure 1 The main categories and functors used in this paper (
![]() $ \mathrm {op}$
indicates the use of the opposite category). Arrows with tails are faithful functors and arrows with two heads in one direction are full. Unlabeled functors are forgetful. The diagram is not fully commutative (even modulo natural isomorphisms).
$ \mathrm {op}$
indicates the use of the opposite category). Arrows with tails are faithful functors and arrows with two heads in one direction are full. Unlabeled functors are forgetful. The diagram is not fully commutative (even modulo natural isomorphisms).
A significant feature of the canonical model
![]() $\texttt {Conc}(X)=(Z_X,\mathcal {B}a(Z_X),\mu _{Z_X})$
of a
$\texttt {Conc}(X)=(Z_X,\mathcal {B}a(Z_X),\mu _{Z_X})$
of a
![]() $\mathbf {PrbAlg}$
-space
$\mathbf {PrbAlg}$
-space
![]() $X=(X,\mu )$
is the strong Lusin property (cf. [Reference Jamneshan and Tao20, §7]), which states that the commutative von Neumann algebra
$X=(X,\mu )$
is the strong Lusin property (cf. [Reference Jamneshan and Tao20, §7]), which states that the commutative von Neumann algebra
![]() $L^\infty (Z_X,\mathcal {B} a(Z_X),\mu _{Z_X})$
is isomorphic to the commutative
$L^\infty (Z_X,\mathcal {B} a(Z_X),\mu _{Z_X})$
is isomorphic to the commutative
![]() $C^{*}$
-algebra
$C^{*}$
-algebra
![]() $C(Z_X)$
of continuous functions on
$C(Z_X)$
of continuous functions on
![]() $Z_X$
in the category of unital
$Z_X$
in the category of unital
![]() $C^{*}$
-algebras. In
$C^{*}$
-algebras. In
![]() ${\mathbf {CHPrb}}$
-spaces with the strong Lusin property, every equivalence class of bounded measurable functions has a continuous representative. A very useful consequence of this property is that it comes with a canonical disintegration of measures.
${\mathbf {CHPrb}}$
-spaces with the strong Lusin property, every equivalence class of bounded measurable functions has a continuous representative. A very useful consequence of this property is that it comes with a canonical disintegration of measures.
Theorem 2.2. Let
![]() $\Gamma $
be a discrete group. Let
$\Gamma $
be a discrete group. Let
![]() $ \pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a
$ \pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism. Then there exists a unique Baire–Radon probability measure
$\mathbf {PrbAlg}_\Gamma $
-morphism. Then there exists a unique Baire–Radon probability measure
![]() $\mu _y$
on
$\mu _y$
on
![]() $Z_{X}$
for each
$Z_{X}$
for each
![]() $y \in Z_{Y}$
, which depends continuously on y in the vague topology in the sense that
$y \in Z_{Y}$
, which depends continuously on y in the vague topology in the sense that
![]() $y \mapsto \int _{Z_{X}} f\,d\mu _y$
is continuous for every f in the space of continuous functions
$y \mapsto \int _{Z_{X}} f\,d\mu _y$
is continuous for every f in the space of continuous functions
![]() $C(Z_{X})$
, and such that
$C(Z_{X})$
, and such that
 $$ \begin{align} \int_{Z_{X}} f(x) g(\texttt{Conc}(\pi)(x))\,d\mu_{Z_{X}}(x) = \int_{Z_{Y}} \bigg(\int_{Z_{X}} f\,d\mu_y\bigg) g\,d\mu_{Z_{Y}} \end{align} $$
$$ \begin{align} \int_{Z_{X}} f(x) g(\texttt{Conc}(\pi)(x))\,d\mu_{Z_{X}}(x) = \int_{Z_{Y}} \bigg(\int_{Z_{X}} f\,d\mu_y\bigg) g\,d\mu_{Z_{Y}} \end{align} $$
for all
![]() $f \in C(Z_{X})$
,
$f \in C(Z_{X})$
,
![]() $g \in C(Z_{Y})$
. Furthermore, for each
$g \in C(Z_{Y})$
. Furthermore, for each
![]() $y \in Z_{Y}$
,
$y \in Z_{Y}$
,
![]() $\mu _y$
is supported on the compact set
$\mu _y$
is supported on the compact set
![]() $\texttt {Conc} (\pi )^{-1}(\{y\})$
, in the sense that
$\texttt {Conc} (\pi )^{-1}(\{y\})$
, in the sense that
![]() $\mu _y(E)=0$
whenever E is a measurable set disjoint from
$\mu _y(E)=0$
whenever E is a measurable set disjoint from
![]() $\texttt {Conc}(\pi )^{-1}(\{y\})$
. (Note that this conclusion does not require the fibers
$\texttt {Conc}(\pi )^{-1}(\{y\})$
. (Note that this conclusion does not require the fibers
![]() $\texttt {Conc} (\pi )^{-1}(\{y\})$
to be Baire measurable.) Moreover, we have
$\texttt {Conc} (\pi )^{-1}(\{y\})$
to be Baire measurable.) Moreover, we have
![]() $ \mu _{S^\gamma _{Z_{Y}}(y)}=(T^\gamma _{Z_{X}})^{*}\mu _y$
for all
$ \mu _{S^\gamma _{Z_{Y}}(y)}=(T^\gamma _{Z_{X}})^{*}\mu _y$
for all
![]() $y\in Z_{Y}$
and
$y\in Z_{Y}$
and
![]() $\gamma \in \Gamma $
.
$\gamma \in \Gamma $
.
Let
![]() $\pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a
$\pi :(X,\mu ,T)\to (Y,\nu ,S)$
be a
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism and let
$\mathbf {PrbAlg}_\Gamma $
-morphism and let
![]() ${\texttt {Conc}(\pi ):Z_{X}\to Z_{Y}}$
be its canonical representation. For every
${\texttt {Conc}(\pi ):Z_{X}\to Z_{Y}}$
be its canonical representation. For every
![]() $f\in L^2(\texttt {Conc}(Y))$
, the composition
$f\in L^2(\texttt {Conc}(Y))$
, the composition
![]() $\texttt {Conc}(\pi )^{*} f$
is an element of
$\texttt {Conc}(\pi )^{*} f$
is an element of
![]() $L^2(\texttt {Conc}(X))$
since
$L^2(\texttt {Conc}(X))$
since
![]() $\texttt {Conc}(\pi )$
is measure-preserving. In fact,
$\texttt {Conc}(\pi )$
is measure-preserving. In fact,
![]() $\{\texttt {Conc}(\pi )^{*} f: f\in L^2(\texttt {Conc }(Y))\}$
is a closed
$\{\texttt {Conc}(\pi )^{*} f: f\in L^2(\texttt {Conc }(Y))\}$
is a closed
![]() $\Gamma $
-invariant subspace of
$\Gamma $
-invariant subspace of
![]() $L^2(\texttt {Conc}(X))$
. Thus, we can identify
$L^2(\texttt {Conc}(X))$
. Thus, we can identify
![]() $L^2(\texttt {Conc}(Y))$
with the closed subspace
$L^2(\texttt {Conc}(Y))$
with the closed subspace
![]() $ \texttt {Conc}(\pi )^{*}(L^2(\texttt {Conc}(Y)))$
in
$ \texttt {Conc}(\pi )^{*}(L^2(\texttt {Conc}(Y)))$
in
![]() $L^2(\texttt {Conc}(X))$
. Using this identification, we can define a conditional expectation operator
$L^2(\texttt {Conc}(X))$
. Using this identification, we can define a conditional expectation operator
![]() $ \mathbb {E}(\cdot |Y)$
from
$ \mathbb {E}(\cdot |Y)$
from
![]() $L^2(\texttt {Conc}(X))$
to
$L^2(\texttt {Conc}(X))$
to
![]() $L^2(\texttt {Conc}(Y))$
. Since
$L^2(\texttt {Conc}(Y))$
. Since
![]() $L^\infty $
is dense in
$L^\infty $
is dense in
![]() $L^2$
in the
$L^2$
in the
![]() $L^2$
topology and by Theorem 2.2, we obtain the disintegration of measures
$L^2$
topology and by Theorem 2.2, we obtain the disintegration of measures
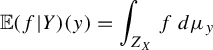 $$ \begin{align*} \mathbb{E}(f|Y)(y)=\int_{Z_{X}} f\,d\mu_y \end{align*} $$
$$ \begin{align*} \mathbb{E}(f|Y)(y)=\int_{Z_{X}} f\,d\mu_y \end{align*} $$
almost surely for all
![]() $f\in L^2(\texttt {Conc}(X))$
.
$f\in L^2(\texttt {Conc}(X))$
.
An important application is a canonical construction of relatively independent products. Indeed, let
![]() $\pi _{1}:(X_{1},\mu _{1},T_{1})\rightarrow (Y,\nu ,S)$
,
$\pi _{1}:(X_{1},\mu _{1},T_{1})\rightarrow (Y,\nu ,S)$
,
![]() $\pi _{2}:(X_{2},\mu _{2},T_{2})\rightarrow (Y,\nu ,S)$
be two
$\pi _{2}:(X_{2},\mu _{2},T_{2})\rightarrow (Y,\nu ,S)$
be two
![]() $\mathbf {PrbAlg}_{\Gamma }$
-morphisms. Let
$\mathbf {PrbAlg}_{\Gamma }$
-morphisms. Let
![]() $(\mu _{y}^{1})_{y\in Z_{Y}}$
and
$(\mu _{y}^{1})_{y\in Z_{Y}}$
and
![]() $(\mu _{y}^{2})_{y\in Z_{Y}}$
be the corresponding canonical disintegration of measures. Define the probability measure
$(\mu _{y}^{2})_{y\in Z_{Y}}$
be the corresponding canonical disintegration of measures. Define the probability measure
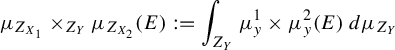 $$ \begin{align*} \mu _{Z_{X_{1}}}\times _{Z_{Y}}\mu _{Z_{X_{2}}}(E):=\int_{Z_{Y}}\mu _{y}^{1}\times \mu _{y}^{2}(E)\,d\mu _{Z_{Y}} \end{align*} $$
$$ \begin{align*} \mu _{Z_{X_{1}}}\times _{Z_{Y}}\mu _{Z_{X_{2}}}(E):=\int_{Z_{Y}}\mu _{y}^{1}\times \mu _{y}^{2}(E)\,d\mu _{Z_{Y}} \end{align*} $$
for all
![]() $E\in \mathcal {B}a(Z_{X_{1}})\otimes \mathcal {B}a(Z_{X_{2}})$
. Then
$E\in \mathcal {B}a(Z_{X_{1}})\otimes \mathcal {B}a(Z_{X_{2}})$
. Then
is a
![]() ${\mathbf {CHPrb}}_{\Gamma }$
-object coming with two
${\mathbf {CHPrb}}_{\Gamma }$
-object coming with two
![]() ${\mathbf {CHPrb}} _{\Gamma }$
-morphisms
${\mathbf {CHPrb}} _{\Gamma }$
-morphisms
![]() ${\psi _{1}:Z_{X_{1}}\times Z_{X_{2}}\rightarrow Z_{X_{1}}}$
and
${\psi _{1}:Z_{X_{1}}\times Z_{X_{2}}\rightarrow Z_{X_{1}}}$
and
![]() $\psi _{2}:Z_{X_{1}}\times Z_{X_{2}}\rightarrow Z_{X_{2}}$
. Applying the functor
$\psi _{2}:Z_{X_{1}}\times Z_{X_{2}}\rightarrow Z_{X_{2}}$
. Applying the functor
![]() $\texttt {Alg}\circ \texttt {Abs}$
, we obtain a
$\texttt {Alg}\circ \texttt {Abs}$
, we obtain a
![]() $\mathbf {PrbAlg}_{\Gamma }$
-object
$\mathbf {PrbAlg}_{\Gamma }$
-object
![]() $(X_{1}\times _{Y}X_{2},\mu _{1}\times _{Y}\mu _{2},T_{1}\times T_{2})$
and the two
$(X_{1}\times _{Y}X_{2},\mu _{1}\times _{Y}\mu _{2},T_{1}\times T_{2})$
and the two
![]() $\mathbf {PrbAlg}_{\Gamma }$
-morphisms
$\mathbf {PrbAlg}_{\Gamma }$
-morphisms
![]() $ \texttt {Alg}\circ \texttt {Abs}(\psi _{1}), \texttt {Alg}\circ \texttt {Abs} (\psi _{2})$
satisfying the following commutative diagram in
$ \texttt {Alg}\circ \texttt {Abs}(\psi _{1}), \texttt {Alg}\circ \texttt {Abs} (\psi _{2})$
satisfying the following commutative diagram in
![]() $\mathbf {PrbAlg} _{\Gamma }$
:
$\mathbf {PrbAlg} _{\Gamma }$
:
2.2 Ultrafilters and non-standard analysis
A filter on a set X is a non-empty collection f of subsets of X satisfying the following properties.
-
(i)
 $\emptyset \notin f$
.
$\emptyset \notin f$
. -
(ii) If
 $A,B\in f$
, then
$A,B\in f$
, then
 $A\cap B\in f$
.
$A\cap B\in f$
. -
(iii) If
 $A\in f$
,
$A\in f$
,
 $B\subset X$
, and
$B\subset X$
, and
 $A\subset B$
, then
$A\subset B$
, then
 $B\in f$
.
$B\in f$
.
An ultrafilter on X is a maximal element in the set of filters on X with respect to set inclusion. A non-principal ultrafilter is an ultrafilter such that none of its elements is finite.
We are concerned with non-principal ultrafilters on the set of natural numbers
![]() $\mathbb {N}$
. The Fréchet filter consists of all subsets
$\mathbb {N}$
. The Fréchet filter consists of all subsets
![]() $A\subset \mathbb {N}$
for which there is
$A\subset \mathbb {N}$
for which there is
![]() $n\in \mathbb {N}$
such that A contains the tail
$n\in \mathbb {N}$
such that A contains the tail
![]() $\{n,n+1,\ldots \}$
. By definition, the Fréchet filter is contained in any non-principal ultrafilter on
$\{n,n+1,\ldots \}$
. By definition, the Fréchet filter is contained in any non-principal ultrafilter on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Fix a non-principal ultrafilter p on
![]() $\mathbb {N}$
. The ultraproduct of a sequence
$\mathbb {N}$
. The ultraproduct of a sequence
![]() $\{X_n\}$
of sets with respect to p is the quotient set
$\{X_n\}$
of sets with respect to p is the quotient set
![]() $X^{*}=\prod _{n\to p} X_n$
of the Cartesian product
$X^{*}=\prod _{n\to p} X_n$
of the Cartesian product
![]() $\prod _{n\in \mathbb {N}} X_n$
with respect to the equivalence relation
$\prod _{n\in \mathbb {N}} X_n$
with respect to the equivalence relation
![]() $(x_n)\sim (y_n)$
if and only if
$(x_n)\sim (y_n)$
if and only if
![]() $\{n\colon x_n=y_n\}\in p$
. The equivalence class of
$\{n\colon x_n=y_n\}\in p$
. The equivalence class of
![]() $(x_n)$
is denoted by
$(x_n)$
is denoted by
![]() $\lim _{n\to p} x_n$
and called an ultralimit of the elements
$\lim _{n\to p} x_n$
and called an ultralimit of the elements
![]() $x_n$
.
$x_n$
.
A subset A of
![]() $X^{*}$
is said to be internal if it is of the form
$X^{*}$
is said to be internal if it is of the form
![]() $A=\prod _{n\to p} A_n$
for some subset
$A=\prod _{n\to p} A_n$
for some subset
![]() $A_n\subset X_n$
for each n. One can check that the collection of internal subsets of
$A_n\subset X_n$
for each n. One can check that the collection of internal subsets of
![]() $X^{*}$
forms an algebra of sets, in particular,
$X^{*}$
forms an algebra of sets, in particular,
![]() $\bigcup _{i=1}^K A_i= \prod _{n\to p} \bigcup _{i=1}^K A_{i,n}$
for finitely many internal subsets
$\bigcup _{i=1}^K A_i= \prod _{n\to p} \bigcup _{i=1}^K A_{i,n}$
for finitely many internal subsets
![]() $A_i$
of
$A_i$
of
![]() $X^{*}$
.
$X^{*}$
.
One can also verify that the ultraproduct of a sequence of groups is a group. Moreover, a class
![]() $\mathfrak {G}$
of groups is said to be uniformly amenable if the ultraproduct group
$\mathfrak {G}$
of groups is said to be uniformly amenable if the ultraproduct group
![]() $\Gamma ^{*}$
is amenable for any sequence of groups
$\Gamma ^{*}$
is amenable for any sequence of groups
![]() $\Gamma _n\in \mathfrak {G}$
.
$\Gamma _n\in \mathfrak {G}$
.
Let
![]() $(r_n)$
be a bounded sequence of real numbers. By the Bolzano–Weierstrass theorem, there is a unique real number r such that
$(r_n)$
be a bounded sequence of real numbers. By the Bolzano–Weierstrass theorem, there is a unique real number r such that
![]() $\lim _{n\to p} (r_n - r)$
is infinitesimal, that is, an ultralimit real number in the equivalence class of a null sequence. We define the standard part function
$\lim _{n\to p} (r_n - r)$
is infinitesimal, that is, an ultralimit real number in the equivalence class of a null sequence. We define the standard part function ![]() .
.
3 Proof of Theorem 1.5
We prove Theorem 1.5 via an ultralimit construction from Theorem 1.10. The following simple lemma is key. Throughout, fix a non-principal ultrafilter p on
![]() $\mathbb {N}$
.
$\mathbb {N}$
.
Lemma 3.1. Let
![]() $\{\Gamma _n\}$
be a sequence of groups and let
$\{\Gamma _n\}$
be a sequence of groups and let
![]() $\Gamma ^{*}=\prod _{n\to p}\Gamma _n$
be their ultraproduct. Let
$\Gamma ^{*}=\prod _{n\to p}\Gamma _n$
be their ultraproduct. Let
![]() $S=\prod _{n\to p} S_n$
be an internal subset of
$S=\prod _{n\to p} S_n$
be an internal subset of
![]() $\Gamma ^{*}$
which is a K-syndetic subset of
$\Gamma ^{*}$
which is a K-syndetic subset of
![]() $\Gamma ^{*}$
for some
$\Gamma ^{*}$
for some
![]() $K\geq 1$
. Then
$K\geq 1$
. Then
Proof. There are
![]() $\gamma _1,\ldots ,\gamma _K\in \Gamma $
such that
$\gamma _1,\ldots ,\gamma _K\in \Gamma $
such that
![]() $\Gamma ^{*}=\bigcup _{i=1}^K \gamma _i \cdot S$
. We have
$\Gamma ^{*}=\bigcup _{i=1}^K \gamma _i \cdot S$
. We have
![]() $\gamma _i=\lim _{n\to p} \gamma _{i,n}$
for some choice of
$\gamma _i=\lim _{n\to p} \gamma _{i,n}$
for some choice of
![]() $\gamma _{i,n}\in \Gamma _n$
for each n and every
$\gamma _{i,n}\in \Gamma _n$
for each n and every
![]() $1\leq i\leq K$
such that
$1\leq i\leq K$
such that
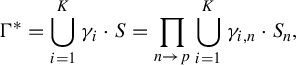 $$ \begin{align*}\Gamma^{*} = \bigcup_{i=1}^K \gamma_i\cdot S = \prod_{n\to p} \bigcup_{i=1}^K \gamma_{i,n}\cdot S_n,\end{align*} $$
$$ \begin{align*}\Gamma^{*} = \bigcup_{i=1}^K \gamma_i\cdot S = \prod_{n\to p} \bigcup_{i=1}^K \gamma_{i,n}\cdot S_n,\end{align*} $$
and thus
![]() $\{n\colon \bigcup _{i=1}^K \gamma _{i,n}\cdot S_n=\Gamma _n\}\in p$
.
$\{n\colon \bigcup _{i=1}^K \gamma _{i,n}\cdot S_n=\Gamma _n\}\in p$
.
At the end of this section, we show how to derive Theorem 1.5 from the following generalization of it.
Theorem 3.2. For every uniformly amenable class
![]() $\mathfrak {G}$
of groups, for all integer
$\mathfrak {G}$
of groups, for all integer
![]() $d\geq 1$
, and any
$d\geq 1$
, and any
![]() $\varepsilon>0$
, there exist an integer
$\varepsilon>0$
, there exist an integer
![]() $K\geq 1$
and
$K\geq 1$
and
![]() $\delta>0$
(only depending on
$\delta>0$
(only depending on
![]() $\mathfrak {G},\varepsilon ,d$
) such that for any group
$\mathfrak {G},\varepsilon ,d$
) such that for any group
![]() $\Gamma \in \mathfrak {G}$
, any probability space
$\Gamma \in \mathfrak {G}$
, any probability space
![]() $(X,\mu )$
, every finitely many pairwise commuting measure-preserving actions
$(X,\mu )$
, every finitely many pairwise commuting measure-preserving actions
![]() $T_i\colon \Gamma \curvearrowright (X,\mu )$
,
$T_i\colon \Gamma \curvearrowright (X,\mu )$
,
![]() $i=1,\ldots ,d$
, and every measurable set E in X with
$i=1,\ldots ,d$
, and every measurable set E in X with
![]() $\mu (E)\geq \varepsilon $
, it holds that
$\mu (E)\geq \varepsilon $
, it holds that
is K-syndetic, where
![]() $T_{[a,b]}^{\gamma }:=T_{a}^{\gamma }\circ T_{a+1}^{\gamma }\circ \cdots \circ T_{b}^{\gamma }$
.
$T_{[a,b]}^{\gamma }:=T_{a}^{\gamma }\circ T_{a+1}^{\gamma }\circ \cdots \circ T_{b}^{\gamma }$
.
Proof. Toward a contradiction, assume there is a uniformly amenable class of groups
![]() $\mathfrak {G}$
,
$\mathfrak {G}$
,
![]() $d\geq 1, \varepsilon>0$
such that for every
$d\geq 1, \varepsilon>0$
such that for every
![]() $n\geq 1$
, there is a group
$n\geq 1$
, there is a group
![]() $\Gamma _n\in \mathfrak {G}$
, d pairwise commuting measure-preserving
$\Gamma _n\in \mathfrak {G}$
, d pairwise commuting measure-preserving
![]() $\Gamma _n$
-actions
$\Gamma _n$
-actions
![]() $T_{n,1},\ldots , T_{n,d}$
on a probability space
$T_{n,1},\ldots , T_{n,d}$
on a probability space
![]() $(X_n, \mathcal {X}_n,\mu _n)$
, and
$(X_n, \mathcal {X}_n,\mu _n)$
, and
![]() $E_{n}\in \mathcal {X}_n$
with
$E_{n}\in \mathcal {X}_n$
with
![]() $\mu _{n}(E_{n})\geq \varepsilon $
such that
$\mu _{n}(E_{n})\geq \varepsilon $
such that
is not n-syndetic.
Let
![]() $X^{*}=\prod _{n\to p} X_n$
be the ultraproduct of the sets
$X^{*}=\prod _{n\to p} X_n$
be the ultraproduct of the sets
![]() $X_n$
and denote by
$X_n$
and denote by
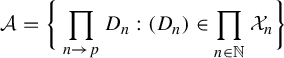 $$ \begin{align*} \mathcal{A}=\bigg\{\prod_{n\to p} D_n: (D_n)\in \prod_{n\in\mathbb{N}} \mathcal{X}_n\bigg\} \end{align*} $$
$$ \begin{align*} \mathcal{A}=\bigg\{\prod_{n\to p} D_n: (D_n)\in \prod_{n\in\mathbb{N}} \mathcal{X}_n\bigg\} \end{align*} $$
the algebra of internal subsets of
![]() $X^{*}$
. We define the Loeb premeasure
$X^{*}$
. We define the Loeb premeasure
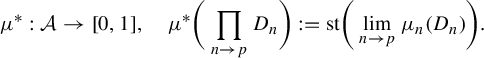 $$ \begin{align*} \mu^{*}:\mathcal{A}\to [0,1], \quad \mu^{*}\bigg(\prod_{n\to p} D_n\bigg):= \mathrm{st}\bigg(\lim_{n\to p} \mu_n(D_n)\bigg). \end{align*} $$
$$ \begin{align*} \mu^{*}:\mathcal{A}\to [0,1], \quad \mu^{*}\bigg(\prod_{n\to p} D_n\bigg):= \mathrm{st}\bigg(\lim_{n\to p} \mu_n(D_n)\bigg). \end{align*} $$
By Carathéodory’s extension and uniqueness theorem,
![]() $\mu ^{*}$
extends to a unique countably additive probability measure
$\mu ^{*}$
extends to a unique countably additive probability measure
![]() $\mu $
on the
$\mu $
on the
![]() $\sigma $
-algebra of sets generated by
$\sigma $
-algebra of sets generated by
![]() $\mathcal {A}$
. By a slight abuse of notation, we let
$\mathcal {A}$
. By a slight abuse of notation, we let
![]() $(X_\mu ,\mu )$
denote the probability algebra associated to
$(X_\mu ,\mu )$
denote the probability algebra associated to
![]() $(X^{*}, \sigma (\mathcal {A}),\mu )$
.
$(X^{*}, \sigma (\mathcal {A}),\mu )$
.
We let
![]() $\Gamma ^{*}=\prod _{n\rightarrow p}\Gamma _n$
. Since
$\Gamma ^{*}=\prod _{n\rightarrow p}\Gamma _n$
. Since
![]() $\mathfrak {G}$
is uniformly amenable,
$\mathfrak {G}$
is uniformly amenable,
![]() $\Gamma ^{*}$
is an amenable group. For each
$\Gamma ^{*}$
is an amenable group. For each
![]() $i=1,\ldots ,d$
, and for every
$i=1,\ldots ,d$
, and for every
![]() $\gamma ^{*}=\lim _{n\to p} \gamma _n \in \Gamma ^{*}$
and
$\gamma ^{*}=\lim _{n\to p} \gamma _n \in \Gamma ^{*}$
and
![]() $\prod _{n\to p} D_n \in \mathcal {A}$
, define
$\prod _{n\to p} D_n \in \mathcal {A}$
, define
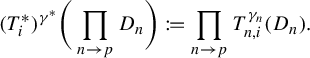
One checks that
![]() $(T^{*}_i)^{\gamma ^{*}}$
is a well-defined
$(T^{*}_i)^{\gamma ^{*}}$
is a well-defined
![]() $\Gamma ^{*}$
-action by Boolean automorphism of
$\Gamma ^{*}$
-action by Boolean automorphism of
![]() $\mathcal {A}$
that preserves the probability measure
$\mathcal {A}$
that preserves the probability measure
![]() $\mu $
. Since
$\mu $
. Since
![]() $\mu $
is a finite measure, by a standard approximation result in measure theory (see, e.g., [Reference Bauer3, Theorem 5.7]), for any
$\mu $
is a finite measure, by a standard approximation result in measure theory (see, e.g., [Reference Bauer3, Theorem 5.7]), for any
![]() $D\in X_\mu $
, there is a sequence
$D\in X_\mu $
, there is a sequence
![]() $D_n\in \mathcal {A}$
such that
$D_n\in \mathcal {A}$
such that
![]() $\mu (D\Delta D_n)\to 0$
as n tends to
$\mu (D\Delta D_n)\to 0$
as n tends to
![]() $\infty $
, where
$\infty $
, where
![]() $\Delta $
denotes symmetric set difference. Thus, we can extend actions
$\Delta $
denotes symmetric set difference. Thus, we can extend actions
![]() $T^{*}_i$
to abstract
$T^{*}_i$
to abstract
![]() $\mathbf {PrbAlg}_\Gamma $
-actions
$\mathbf {PrbAlg}_\Gamma $
-actions
![]() $T_i:\Gamma ^{*}\to \mathrm {Aut}(X_\mu ,\mu )$
. We obtain an abstract
$T_i:\Gamma ^{*}\to \mathrm {Aut}(X_\mu ,\mu )$
. We obtain an abstract
![]() $(\Gamma ^{*})^d$
-system
$(\Gamma ^{*})^d$
-system
![]() $(X_\mu ,\mu ,T)$
.
$(X_\mu ,\mu ,T)$
.
By construction, we have
![]() $\mu (E^{\ast })\geq \varepsilon $
, where
$\mu (E^{\ast })\geq \varepsilon $
, where
![]() $E^{\ast }:=\prod _{n\rightarrow p}E_{n}$
and the
$E^{\ast }:=\prod _{n\rightarrow p}E_{n}$
and the
![]() $E_{n}$
are as in equation (5). By Theorem 1.10, there exist
$E_{n}$
are as in equation (5). By Theorem 1.10, there exist
![]() $\delta>0$
and
$\delta>0$
and
![]() $K\geq 1$
such that
$K\geq 1$
such that
is K-syndetic. Let
By construction, we have
![]() $B=\prod _{n\to p} B_n$
. Then Lemma 3.1 gives
$B=\prod _{n\to p} B_n$
. Then Lemma 3.1 gives
Moreover,
![]() $B_n\subset A_n$
as long as
$B_n\subset A_n$
as long as
![]() $n> {1}/{\delta }$
, and since the Fréchet filter is contained in any non-principal ultrafilter, we must have
$n> {1}/{\delta }$
, and since the Fréchet filter is contained in any non-principal ultrafilter, we must have
![]() $\{n\colon B_n\subset A_n\}\in p$
. Since a filter is intersection closed and p does not contain finite sets as a non-principal ultrafilter, there are infinitely many
$\{n\colon B_n\subset A_n\}\in p$
. Since a filter is intersection closed and p does not contain finite sets as a non-principal ultrafilter, there are infinitely many
![]() $A_n$
which are K-syndetic, which contradicts our assumptions.
$A_n$
which are K-syndetic, which contradicts our assumptions.
As a corollary, we obtain Theorem 1.5.
Proof. By Theorem 3.2, it suffices to verify that the class of solvable groups of derived length at most l is uniformly amenable for some fixed
![]() $l\geq 1$
.
$l\geq 1$
.
Let
![]() $\Gamma ^{*}$
be the ultraproduct of a sequence
$\Gamma ^{*}$
be the ultraproduct of a sequence
![]() $\{\Gamma _n\}$
of solvable groups of derived length at most l. We claim that
$\{\Gamma _n\}$
of solvable groups of derived length at most l. We claim that
![]() $\Gamma ^{*}$
is solvable (and amenable in particular). The direct product
$\Gamma ^{*}$
is solvable (and amenable in particular). The direct product
![]() $\prod _{n}\Gamma _n$
is a solvable group as
$\prod _{n}\Gamma _n$
is a solvable group as
![]() $\{\Gamma _n\}$
has uniformly bounded length. The ultraproduct
$\{\Gamma _n\}$
has uniformly bounded length. The ultraproduct
![]() $\Gamma ^{*}=\prod _{n\rightarrow p}\Gamma _n$
is a quotient group of
$\Gamma ^{*}=\prod _{n\rightarrow p}\Gamma _n$
is a quotient group of
![]() $\prod _{n}\Gamma _n$
so
$\prod _{n}\Gamma _n$
so
![]() $\Gamma ^{*}$
is solvable as well.
$\Gamma ^{*}$
is solvable as well.
4 Proof of Theorem 1.10
Austin [Reference Austin2] proved a subcase of Theorem 1.10 when the acting group
![]() $\Gamma $
is countable and the space
$\Gamma $
is countable and the space
![]() $(X,\mu )$
is standard Lebesgue by constructing characteristic spaces on stated extensions. Our proof of Theorem 1.10 aims to facilitate Austin’s proof [Reference Austin2] to be carried out in a setup where spaces may not be standard Lebesgue and groups may not be countable. We will reuse most of the arguments of Austin [Reference Austin2] and only modify the steps in which the assumptions about the space and the group are substantially used. We will now use the notation introduced in §2.1.
$(X,\mu )$
is standard Lebesgue by constructing characteristic spaces on stated extensions. Our proof of Theorem 1.10 aims to facilitate Austin’s proof [Reference Austin2] to be carried out in a setup where spaces may not be standard Lebesgue and groups may not be countable. We will reuse most of the arguments of Austin [Reference Austin2] and only modify the steps in which the assumptions about the space and the group are substantially used. We will now use the notation introduced in §2.1.
Throughout this section, we let
![]() $\Gamma $
be a (discrete) amenable group and
$\Gamma $
be a (discrete) amenable group and
![]() $(\Phi _\kappa )$
be a left Følner net for
$(\Phi _\kappa )$
be a left Følner net for
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $(X,\mu )$
be a
$(X,\mu )$
be a
![]() ${\mathbf {PrbAlg}}$
-space and
${\mathbf {PrbAlg}}$
-space and
![]() $T_{1},T_{2},\ldots ,T_{d}$
be commuting group homomorphisms
$T_{1},T_{2},\ldots ,T_{d}$
be commuting group homomorphisms
![]() $T_{i}\colon \Gamma \rightarrow \mathrm {Aut}(X,\mu )$
, that is,
$T_{i}\colon \Gamma \rightarrow \mathrm {Aut}(X,\mu )$
, that is,
![]() $T_{i}^{\gamma }\circ T_{j}^{\eta }=T_{j}^{\eta }\circ T_{i}^{\gamma }$
for all
$T_{i}^{\gamma }\circ T_{j}^{\eta }=T_{j}^{\eta }\circ T_{i}^{\gamma }$
for all
![]() $\gamma ,\eta \in \Gamma $
and
$\gamma ,\eta \in \Gamma $
and
![]() $1\leq i<j\leq d$
(the automorphism group
$1\leq i<j\leq d$
(the automorphism group
![]() $\mathrm {Aut}(X,\mu )$
is taken in the category
$\mathrm {Aut}(X,\mu )$
is taken in the category
![]() $\mathbf {PrbAlg}$
). We denote by
$\mathbf {PrbAlg}$
). We denote by
![]() $(\tilde {X},\tilde {\mu },\tilde {T})$
the corresponding canonical model, so that
$(\tilde {X},\tilde {\mu },\tilde {T})$
the corresponding canonical model, so that
![]() $\tilde {X}$
is a compact Hausdorff space and each
$\tilde {X}$
is a compact Hausdorff space and each
![]() $\tilde {T}_{i}$
acts on
$\tilde {T}_{i}$
acts on
![]() $(\tilde {X},\tilde {\mu })$
by measure-preserving homeomorphisms. This canonical model has the advantage that tools such as disintegration of measure and relative independent product are available as discussed in §2.1. For the most part, we can then adopt Austin’s arguments on the concrete space
$(\tilde {X},\tilde {\mu })$
by measure-preserving homeomorphisms. This canonical model has the advantage that tools such as disintegration of measure and relative independent product are available as discussed in §2.1. For the most part, we can then adopt Austin’s arguments on the concrete space
![]() $(\tilde {X},\tilde {\mu },\tilde {T})$
. Then the corresponding results for the probability algebra
$(\tilde {X},\tilde {\mu },\tilde {T})$
. Then the corresponding results for the probability algebra
![]() $(X,\mu )$
follow by applying the functor
$(X,\mu )$
follow by applying the functor
![]() $\texttt {Alg}\circ \texttt {Abs}$
.
$\texttt {Alg}\circ \texttt {Abs}$
.
We begin with Zorin-Kranich’s convergence theorem [Reference Zorin-Kranich26] which holds in the generality that we have just set up.
Theorem 4.1. (Zorin-Kranich’s convergence theorem)
Let
![]() $f_{1},f_{2},\ldots ,f_{d}\in L^{\infty }(X,\mu ) $
. Then the limit
$f_{1},f_{2},\ldots ,f_{d}\in L^{\infty }(X,\mu ) $
. Then the limit
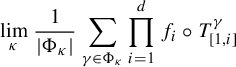 $$ \begin{align*} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\prod_{i=1}^{d}f_{i}\circ T_{[1,i]}^{\gamma } \end{align*} $$
$$ \begin{align*} \lim_{\kappa}\frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\prod_{i=1}^{d}f_{i}\circ T_{[1,i]}^{\gamma } \end{align*} $$
exists in
![]() $L^{2}(X,\mu )$
and is independent of the choice of the (left) Følner net
$L^{2}(X,\mu )$
and is independent of the choice of the (left) Følner net
![]() $(\Phi _{\kappa })$
.
$(\Phi _{\kappa })$
.
This is exactly the claim in equation (1) in Theorem 1.10. It remains to prove the claim in equation (2) in the same theorem. This is achieved as follows. Consider the set of d-fold couplings on
![]() $\tilde {X}^{d}$
, which is the collection of Baire probability measures on
$\tilde {X}^{d}$
, which is the collection of Baire probability measures on
![]() $(\tilde {X}^{d},\mathcal {B}a(\tilde {X}^{d}))$
all of whose coordinate projections are
$(\tilde {X}^{d},\mathcal {B}a(\tilde {X}^{d}))$
all of whose coordinate projections are
![]() $\tilde {\mu }$
. By Theorem 4.1, for each
$\tilde {\mu }$
. By Theorem 4.1, for each
![]() $x\in \tilde {X}$
, the averages
$x\in \tilde {X}$
, the averages
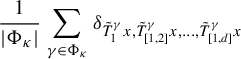 $$ \begin{align*} \frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\delta _{\tilde{T} _{1}^{\gamma }x,\tilde{T}_{[1,2]}^{\gamma }x,\ldots ,\tilde{T} _{[1,d]}^{\gamma }x} \end{align*} $$
$$ \begin{align*} \frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\delta _{\tilde{T} _{1}^{\gamma }x,\tilde{T}_{[1,2]}^{\gamma }x,\ldots ,\tilde{T} _{[1,d]}^{\gamma }x} \end{align*} $$
converge weakly to a measure
![]() $\unicode{x3bb} $
in the set of d-fold couplings. This weak convergence implies that
$\unicode{x3bb} $
in the set of d-fold couplings. This weak convergence implies that
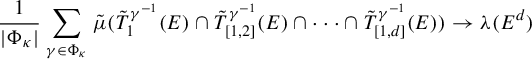 $$ \begin{align*} \frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\tilde{\mu}(\tilde{T} _{1}^{\gamma ^{-1}}(E)\cap \tilde{T}_{[1,2]}^{\gamma ^{-1}}(E)\cap \cdots \cap \tilde{T}_{[1,d]}^{\gamma ^{-1}}(E))\rightarrow \unicode{x3bb} (E^{d}) \end{align*} $$
$$ \begin{align*} \frac{1}{|\Phi _{\kappa}|}\sum_{\gamma \in \Phi _{\kappa}}\tilde{\mu}(\tilde{T} _{1}^{\gamma ^{-1}}(E)\cap \tilde{T}_{[1,2]}^{\gamma ^{-1}}(E)\cap \cdots \cap \tilde{T}_{[1,d]}^{\gamma ^{-1}}(E))\rightarrow \unicode{x3bb} (E^{d}) \end{align*} $$
for all
![]() $E\in \mathcal {B}a(\tilde {X})$
. To establish multiple recurrence, it suffices to show that
$E\in \mathcal {B}a(\tilde {X})$
. To establish multiple recurrence, it suffices to show that
Austin first introduces the notion of satedness and proves that any space has an extension that is sated. It is then not a loss of generality to assume that
![]() $(\tilde {X},\tilde {\mu })$
is a sated space in the first place. The advantage of a sated space is that it constrains how a certain relevant
$(\tilde {X},\tilde {\mu })$
is a sated space in the first place. The advantage of a sated space is that it constrains how a certain relevant
![]() $\sigma $
-subalgebra of the space is lifted to any of its extensions. More about satedness can be found in §4.1.
$\sigma $
-subalgebra of the space is lifted to any of its extensions. More about satedness can be found in §4.1.
Define
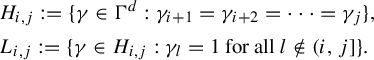 $$ \begin{align*} &H_{i,j} : =\{\mathbf{\gamma}\in \Gamma^{d}:\gamma_{i+1}=\gamma_{i+2}=\cdots =\gamma_{j}\}, \\ &L_{i,j} : =\{\mathbf{\gamma}\in H_{i,j}:\gamma_{l}=1\ \text{for all}\ l\notin (i,j]\}. \end{align*} $$
$$ \begin{align*} &H_{i,j} : =\{\mathbf{\gamma}\in \Gamma^{d}:\gamma_{i+1}=\gamma_{i+2}=\cdots =\gamma_{j}\}, \\ &L_{i,j} : =\{\mathbf{\gamma}\in H_{i,j}:\gamma_{l}=1\ \text{for all}\ l\notin (i,j]\}. \end{align*} $$
Austin then constructs recursively a tower of
![]() $\Gamma ^{d}$
-spaces, as a variant of Host–Kra self-joinings [Reference Host16, Reference Host and Kra17]:
$\Gamma ^{d}$
-spaces, as a variant of Host–Kra self-joinings [Reference Host16, Reference Host and Kra17]:
Assume that the tower has already been constructed up to some
![]() $j\leq d-1$
. Define an
$j\leq d-1$
. Define an
![]() $H_{d-j-1,d}$
-action
$H_{d-j-1,d}$
-action
![]() $\tilde {R}^{(j)}$
on
$\tilde {R}^{(j)}$
on
![]() $(\tilde {Y}^{(j)}, \tilde {\nu }^{(j)})$
by setting
$(\tilde {Y}^{(j)}, \tilde {\nu }^{(j)})$
by setting
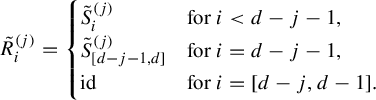 $$ \begin{align*} \tilde{R}_{i}^{(j)}= \begin{cases} \tilde{S}_{i}^{(j)} & \text{for }i<d-j-1, \\ \tilde{S}_{[d-j-1,d]}^{(j)} & \text{for }i=d-j-1, \\ \text{id} & \text{for }i=[d-j,d-1]. \end{cases} \end{align*} $$
$$ \begin{align*} \tilde{R}_{i}^{(j)}= \begin{cases} \tilde{S}_{i}^{(j)} & \text{for }i<d-j-1, \\ \tilde{S}_{[d-j-1,d]}^{(j)} & \text{for }i=d-j-1, \\ \text{id} & \text{for }i=[d-j,d-1]. \end{cases} \end{align*} $$
An
![]() $H_{d-j-1,d}$
-space is then constructed by the relative product
$H_{d-j-1,d}$
-space is then constructed by the relative product
where for a subgroup H of
![]() $\Gamma ^d$
, we let
$\Gamma ^d$
, we let
![]() $(\tilde {S})_H$
be the restriction of an action
$(\tilde {S})_H$
be the restriction of an action
![]() $\tilde {S}$
by
$\tilde {S}$
by
![]() $\Gamma ^d$
to an action by H, and for a subgroup L of
$\Gamma ^d$
to an action by H, and for a subgroup L of
![]() $\Gamma ^d$
, we denote by
$\Gamma ^d$
, we denote by
![]() $\Sigma _{\tilde {Y}}^L$
the
$\Sigma _{\tilde {Y}}^L$
the
![]() $\sigma $
-subalgebra of
$\sigma $
-subalgebra of
![]() $\Sigma _{\tilde Y}$
of invariant sets with respect to the restriction of an action
$\Sigma _{\tilde Y}$
of invariant sets with respect to the restriction of an action
![]() $\tilde {S}$
by
$\tilde {S}$
by
![]() $\Gamma ^d$
to an action by L.
$\Gamma ^d$
to an action by L.
Finally, a lifting lemma proves the existence of a
![]() $\Gamma ^d$
-space extension
$\Gamma ^d$
-space extension
which admits a commutative diagram of
![]() $H_{d-j-1,d}$
-spaces
$H_{d-j-1,d}$
-spaces
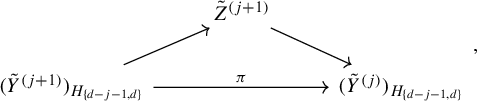
where
![]() $Y_H$
is the H-space with the same probability space but with the action restricted to H.
$Y_H$
is the H-space with the same probability space but with the action restricted to H.
The advantage of the sequence of extensions is a variant of Host–Kra inequality: the asymptotic behavior of the ergodic average of
![]() $f_{i}$
(the term inside the limit of equation (1)) is governed by an integral of a product of those
$f_{i}$
(the term inside the limit of equation (1)) is governed by an integral of a product of those
![]() $f_{i}$
lifted to
$f_{i}$
lifted to
![]() $\tilde {Y}^{(d)}$
.
$\tilde {Y}^{(d)}$
.
These Host–Kra-like self-joinings admit characteristic subspaces. A closed subspace
![]() $V\leq L^{2}(\tilde {\mu })$
is partially characteristic in position i if the ergodic averages of
$V\leq L^{2}(\tilde {\mu })$
is partially characteristic in position i if the ergodic averages of
![]() $f_{1},\ldots ,f_{d}$
are asymptotically the same as those of
$f_{1},\ldots ,f_{d}$
are asymptotically the same as those of
![]() $ f_{1},\ldots ,f_{i-1},P^{V}f_{i},f_{i+1},\ldots ,f_{d}$
, where
$ f_{1},\ldots ,f_{i-1},P^{V}f_{i},f_{i+1},\ldots ,f_{d}$
, where
![]() $P^V$
denotes the orthogonal projection onto the space V. In a sated space
$P^V$
denotes the orthogonal projection onto the space V. In a sated space
![]() $(\tilde {X},\tilde {\mu })$
, it can be proven that
$(\tilde {X},\tilde {\mu })$
, it can be proven that
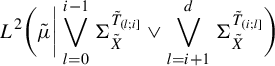 $$ \begin{align*} L^{2}\bigg( \tilde{\mu} \bigg|\bigvee\limits_{l=0}^{i-1}\Sigma^{\tilde{T}_{(l;i]}}_{\tilde{X}}\vee \bigvee\limits_{l=i+1}^{d}\Sigma ^{\tilde{T}_{(i;l]}}_{\tilde{X}}\bigg) \end{align*} $$
$$ \begin{align*} L^{2}\bigg( \tilde{\mu} \bigg|\bigvee\limits_{l=0}^{i-1}\Sigma^{\tilde{T}_{(l;i]}}_{\tilde{X}}\vee \bigvee\limits_{l=i+1}^{d}\Sigma ^{\tilde{T}_{(i;l]}}_{\tilde{X}}\bigg) \end{align*} $$
is partially characteristic in position i. The significance of these characteristic subspaces is that
![]() $P^Vf_d$
can be approximated by a finite sum of products of the form
$P^Vf_d$
can be approximated by a finite sum of products of the form
![]() $h_0h_1\ldots h_{d-1}$
, where each
$h_0h_1\ldots h_{d-1}$
, where each
![]() $h_i$
is
$h_i$
is
![]() $\Sigma ^{\tilde {T}_{(i;d]}}_{\tilde {X}}$
-measurable. This then allows us to reduce an ergodic average of d functions to an ergodic average of
$\Sigma ^{\tilde {T}_{(i;d]}}_{\tilde {X}}$
-measurable. This then allows us to reduce an ergodic average of d functions to an ergodic average of
![]() $d-1$
functions.
$d-1$
functions.
Satedness helps to prove that some spaces related to the characteristic subspaces are relatively orthogonal. As an illustrative example, let us say we want to prove that
![]() $L^{2}(\tilde {\mu }|\Phi _{1})$
and
$L^{2}(\tilde {\mu }|\Phi _{1})$
and
![]() $L^{2}(\tilde {\mu }|\Phi _{2})$
are relatively independent over
$L^{2}(\tilde {\mu }|\Phi _{2})$
are relatively independent over
![]() $V(\tilde {X})$
, where
$V(\tilde {X})$
, where
![]() $\Phi _{1},\Phi _{2}$
are
$\Phi _{1},\Phi _{2}$
are
![]() $\sigma $
-algebras over
$\sigma $
-algebras over
![]() $\tilde {X}$
and
$\tilde {X}$
and
![]() $V(\cdot )$
is a functorial
$V(\cdot )$
is a functorial
![]() $L^2$
-subspace (
$L^2$
-subspace (
![]() $V(\tilde {Z})$
is an
$V(\tilde {Z})$
is an
![]() $L^2$
-subspace of
$L^2$
-subspace of
![]() $L^2(\tilde {Z})$
; see Definition 4.3 for details). We assume that
$L^2(\tilde {Z})$
; see Definition 4.3 for details). We assume that
![]() $\tilde X$
is a
$\tilde X$
is a
![]() $\Psi $
-sated space.
$\Psi $
-sated space.
Let
![]() $f\in L^{2}(\tilde {\mu }|\Phi _{1})$
and
$f\in L^{2}(\tilde {\mu }|\Phi _{1})$
and
![]() $g\in L^{2}(\tilde {\mu }|\Phi _{2})$
. We construct a relative product measure
$g\in L^{2}(\tilde {\mu }|\Phi _{2})$
. We construct a relative product measure
and carefully define a
![]() $\Gamma $
-action on the space. Let
$\Gamma $
-action on the space. Let
![]() $\beta _1$
and
$\beta _1$
and
![]() $\beta _2$
be the projections of
$\beta _2$
be the projections of
![]() $\tilde {Y}=\tilde {X}^2$
onto the first and second coordinate, respectively. Since f is
$\tilde {Y}=\tilde {X}^2$
onto the first and second coordinate, respectively. Since f is
![]() $\Phi _{1}$
-measurable, we have
$\Phi _{1}$
-measurable, we have
Then we use V-satedness of
![]() $\tilde {X}$
, which gives that
$\tilde {X}$
, which gives that
![]() $L^{2}(\tilde {\mu })\circ \beta _{1}$
and
$L^{2}(\tilde {\mu })\circ \beta _{1}$
and
![]() $V(\tilde {Y})$
are relatively orthogonal over
$V(\tilde {Y})$
are relatively orthogonal over
![]() $V(\tilde {X})\circ \beta _{1}$
. We will need
$V(\tilde {X})\circ \beta _{1}$
. We will need
![]() $g\circ \beta _{2}\in V(\tilde {Y})$
, so equation (7) equals
$g\circ \beta _{2}\in V(\tilde {Y})$
, so equation (7) equals
By the same line of reasoning as in equation (7), we have this equals
as desired.
From here, Austin’s ergodic version of Tao’s removal lemma [Reference Tao23] yields equation (6).
The modifications we need to extend these arguments to our uncountable setup are as follows.
-
(i) Construction of sated extensions for
 ${\mathbf {PrbAlg}}$
-spaces.
${\mathbf {PrbAlg}}$
-spaces. -
(ii) Lifting lemma: extending a factor map relative to a subgroup to the whole group for
 ${\mathbf {PrbAlg}}$
-spaces and for uncountable groups.
${\mathbf {PrbAlg}}$
-spaces and for uncountable groups.
These modifications are carried out in the following two subsections.
4.1
 $\mathbf {PrbAlg}_\Gamma $
-sated extensions
$\mathbf {PrbAlg}_\Gamma $
-sated extensions
In this section, we verify that probability algebra dynamical systems admit sated extensions.
Following the standard notation, if
![]() $\pi :(Y,\nu ,S)\rightarrow (X,\mu ,T)$
is an extension, we let
$\pi :(Y,\nu ,S)\rightarrow (X,\mu ,T)$
is an extension, we let
![]() ${\pi }^{*} f:=f\circ \pi $
on
${\pi }^{*} f:=f\circ \pi $
on
![]() $L^2(X)$
. If
$L^2(X)$
. If
![]() ${\mathcal {H}}$
is a closed subspace of a Hilbert space, we denote by
${\mathcal {H}}$
is a closed subspace of a Hilbert space, we denote by
![]() $P_{\mathcal {H}}$
the orthogonal projection onto
$P_{\mathcal {H}}$
the orthogonal projection onto
![]() $\mathcal {H}$
.
$\mathcal {H}$
.
Recall that if
![]() ${\mathcal {H}}_1,{\mathcal {H}}_2$
, and
${\mathcal {H}}_1,{\mathcal {H}}_2$
, and
![]() ${\mathcal {I}}$
are closed subspaces of a Hilbert space, then
${\mathcal {I}}$
are closed subspaces of a Hilbert space, then
![]() ${\mathcal {H}}_1$
and
${\mathcal {H}}_1$
and
![]() ${\mathcal {H}}_2$
are said to be relatively orthogonal over
${\mathcal {H}}_2$
are said to be relatively orthogonal over
![]() $\mathcal {I}$
if for any
$\mathcal {I}$
if for any
![]() $u\in \mathcal {H}_1$
and
$u\in \mathcal {H}_1$
and
![]() $v\in \mathcal {H}_2$
, we have
$v\in \mathcal {H}_2$
, we have
![]() $\langle u,v\rangle =\langle P_{\mathcal {I}}u, P_{\mathcal {I} }v\rangle $
. The following simple characterization of relative orthogonality will be useful.
$\langle u,v\rangle =\langle P_{\mathcal {I}}u, P_{\mathcal {I} }v\rangle $
. The following simple characterization of relative orthogonality will be useful.
Lemma 4.2. Suppose
![]() $\mathcal {H}_1,\mathcal {H}_2$
, and
$\mathcal {H}_1,\mathcal {H}_2$
, and
![]() $\mathcal {I}$
are closed subspaces of a Hilbert space. If in addition
$\mathcal {I}$
are closed subspaces of a Hilbert space. If in addition
![]() $\mathcal {I}\subset \mathcal {H}_2$
, then
$\mathcal {I}\subset \mathcal {H}_2$
, then
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
are relatively orthogonal over
$\mathcal {H}_2$
are relatively orthogonal over
![]() $\mathcal {I}$
if and only if for any
$\mathcal {I}$
if and only if for any
![]() $u\in \mathcal {H}_1$
,
$u\in \mathcal {H}_1$
,
![]() $ P_{\mathcal {I}}(u)=P_{\mathcal {H}_2}(u)$
.
$ P_{\mathcal {I}}(u)=P_{\mathcal {H}_2}(u)$
.
Proof. Suppose
![]() $\mathcal {H}_1$
and
$\mathcal {H}_1$
and
![]() $\mathcal {H}_2$
are relatively orthogonal over
$\mathcal {H}_2$
are relatively orthogonal over
![]() $ \mathcal {I}$
. Fix
$ \mathcal {I}$
. Fix
![]() $u\in \mathcal {H}_1$
. For any
$u\in \mathcal {H}_1$
. For any
![]() $v\in \mathcal {H}_2$
,
$v\in \mathcal {H}_2$
,
![]() $ \langle u,v\rangle =\langle P_{\mathcal {I}}u, P_{\mathcal {I} }v\rangle =\langle P_{\mathcal {I}}u, v\rangle $
. Since
$ \langle u,v\rangle =\langle P_{\mathcal {I}}u, P_{\mathcal {I} }v\rangle =\langle P_{\mathcal {I}}u, v\rangle $
. Since
![]() $P_{\mathcal {I}}u\in \mathcal {H}_2$
, we have
$P_{\mathcal {I}}u\in \mathcal {H}_2$
, we have
![]() $P_{\mathcal {H}_2}u=P_{\mathcal {H} _2}(P_{\mathcal {I}}u)=P_{\mathcal {I}}u$
.
$P_{\mathcal {H}_2}u=P_{\mathcal {H} _2}(P_{\mathcal {I}}u)=P_{\mathcal {I}}u$
.
Conversely, suppose for any vector in
![]() $\mathcal {H}_1$
, its projection onto
$\mathcal {H}_1$
, its projection onto
![]() $ \mathcal {I}$
and
$ \mathcal {I}$
and
![]() ${\mathcal {H}_2}$
are the same. For any
${\mathcal {H}_2}$
are the same. For any
![]() $u\in \mathcal {H}_1$
and
$u\in \mathcal {H}_1$
and
![]() $v\in \mathcal {H}_2$
, we have
$v\in \mathcal {H}_2$
, we have
as desired.
Definition 4.3. (
 $\mathbf {PrbAlg}_\Gamma $
-sated extensions)
$\mathbf {PrbAlg}_\Gamma $
-sated extensions)
A functorial
![]() $L^2$
-subspace of
$L^2$
-subspace of
![]() $\mathbf {PrbAlg} _\Gamma $
-spaces is a composition of functors
$\mathbf {PrbAlg} _\Gamma $
-spaces is a composition of functors
![]() $V=W\circ L^2$
, where W is a functor from the category
$V=W\circ L^2$
, where W is a functor from the category
![]() $\mathbf {Hilb}_\Gamma $
to
$\mathbf {Hilb}_\Gamma $
to
![]() $\mathbf {Hilb}$
sending any object
$\mathbf {Hilb}$
sending any object
![]() $\mathcal {H}$
to a closed subspace
$\mathcal {H}$
to a closed subspace
![]() $V(\mathcal {H})$
of
$V(\mathcal {H})$
of
![]() $\mathcal {H }$
and any morphism
$\mathcal {H }$
and any morphism
![]() $\phi $
from a
$\phi $
from a
![]() $\mathbf {Hilb}_\Gamma $
-object
$\mathbf {Hilb}_\Gamma $
-object
![]() $\mathcal {H}$
to a
$\mathcal {H}$
to a
![]() $\mathbf {Hilb}_\Gamma $
-object
$\mathbf {Hilb}_\Gamma $
-object
![]() $\mathcal {K}$
to the restriction
$\mathcal {K}$
to the restriction
![]() $ V(\phi ):V(\mathcal {H})\to V(\mathcal {K})$
.
$ V(\phi ):V(\mathcal {H})\to V(\mathcal {K})$
.
Let V be a functorial
![]() $L^2$
-subspace of
$L^2$
-subspace of
![]() $\mathbf {PrbAlg}_\Gamma $
-spaces. A
$\mathbf {PrbAlg}_\Gamma $
-spaces. A
![]() $\mathbf {PrbAlg}_\Gamma $
-space
$\mathbf {PrbAlg}_\Gamma $
-space
![]() $X=(X,\mu )$
is said to be V-sated if for any
$X=(X,\mu )$
is said to be V-sated if for any
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism
$\mathbf {PrbAlg}_\Gamma $
-morphism
![]() $\pi :(Y,\nu )\rightarrow (X,\mu )$
, the subspaces
$\pi :(Y,\nu )\rightarrow (X,\mu )$
, the subspaces
![]() $\pi ^{*}(L^2(X))$
and
$\pi ^{*}(L^2(X))$
and
![]() $V(Y)$
of
$V(Y)$
of
![]() $L^2(Y)$
are relatively orthogonal over their common further subspace
$L^2(Y)$
are relatively orthogonal over their common further subspace
![]() $\pi ^{*}(V(X))$
. The condition is equivalent to
$\pi ^{*}(V(X))$
. The condition is equivalent to
![]() $\pi ^{*}(P_{V(X )}(h))=P_{V(Y)}(\pi ^{*}(h))$
for any
$\pi ^{*}(P_{V(X )}(h))=P_{V(Y)}(\pi ^{*}(h))$
for any
![]() $h\in L^2(X )$
, by Lemma 4.2 and the inclusion relation
$h\in L^2(X )$
, by Lemma 4.2 and the inclusion relation
![]() $\pi ^{*}(V(X )) \subset V(Y)$
. Moreover, a
$\pi ^{*}(V(X )) \subset V(Y)$
. Moreover, a
![]() $\mathbf{PrbAlg}_\Gamma $
-morphism
$\mathbf{PrbAlg}_\Gamma $
-morphism
![]() $\pi :(Y,\nu )\rightarrow (X,\mu )$
is said to be relatively V-sated if for any further
$\pi :(Y,\nu )\rightarrow (X,\mu )$
is said to be relatively V-sated if for any further
![]() $\mathbf {PrbAlg} _\Gamma $
-morphism
$\mathbf {PrbAlg} _\Gamma $
-morphism
![]() $\psi : (Z,\unicode{x3bb} )\rightarrow (Y,\nu )$
, the subspaces
$\psi : (Z,\unicode{x3bb} )\rightarrow (Y,\nu )$
, the subspaces
![]() $ (\pi \circ \psi )^{*}(L^2(X))$
and
$ (\pi \circ \psi )^{*}(L^2(X))$
and
![]() $V(Z)$
are relatively orthogonal over
$V(Z)$
are relatively orthogonal over
![]() $ \psi ^{*}(V(Y))$
.
$ \psi ^{*}(V(Y))$
.
For the remainder of this section, we fix a functorial
![]() $L^2$
-subspace V.
$L^2$
-subspace V.
Lemma 4.4. Suppose that
![]() $\pi :Y\rightarrow X $
is a relatively V-sated
$\pi :Y\rightarrow X $
is a relatively V-sated
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism and
$\mathbf {PrbAlg}_\Gamma $
-morphism and
![]() $\phi :Z\rightarrow Y$
is a
$\phi :Z\rightarrow Y$
is a
![]() $ \mathbf {PrbAlg}_\Gamma $
-morphism. Then
$ \mathbf {PrbAlg}_\Gamma $
-morphism. Then
![]() $\pi \circ \phi : Z\rightarrow X $
is relatively V-sated.
$\pi \circ \phi : Z\rightarrow X $
is relatively V-sated.
Proof. Let
![]() $\psi :W\rightarrow Z$
be a
$\psi :W\rightarrow Z$
be a
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism. Fix
$\mathbf {PrbAlg}_\Gamma $
-morphism. Fix
![]() $f\in L^2(X )$
and
$f\in L^2(X )$
and
![]() $g\in V(W)$
. We want to show
$g\in V(W)$
. We want to show
(see Figure 2). Applying the definition of relative satedness of
![]() $Y\overset {\pi }{\rightarrow }X $
to the further extension
$Y\overset {\pi }{\rightarrow }X $
to the further extension
![]() $W \overset {\phi \circ \psi }{\rightarrow }Y$
, we have
$W \overset {\phi \circ \psi }{\rightarrow }Y$
, we have
It remains to prove
![]() $P_{V(Z)}((\pi \circ \phi )^{*}f)=\phi ^{*}P_{V(Y)}(\pi ^{*}f)$
. By the relative satedness of
$P_{V(Z)}((\pi \circ \phi )^{*}f)=\phi ^{*}P_{V(Y)}(\pi ^{*}f)$
. By the relative satedness of
![]() $Y\overset {\pi }{\rightarrow }X $
applied to the further extension
$Y\overset {\pi }{\rightarrow }X $
applied to the further extension
![]() $Z\overset {\phi }{\rightarrow }Y$
,
$Z\overset {\phi }{\rightarrow }Y$
,
![]() $V (Z)$
and
$V (Z)$
and
![]() $ (\pi \circ \phi )^{*}(L^2(X ))$
are relatively orthogonal over
$ (\pi \circ \phi )^{*}(L^2(X ))$
are relatively orthogonal over
![]() $\phi ^{*}(V(Y))$
. Lemma 4.2 gives the desired result.
$\phi ^{*}(V(Y))$
. Lemma 4.2 gives the desired result.
Lemma 4.5. Let
![]() $(A,\leq )$
be a directed set with no maximal element and
$(A,\leq )$
be a directed set with no maximal element and
![]() $ ((X_\alpha )_{\alpha \in A}, (\pi _{\alpha _1,\alpha _2})_{\alpha _1,\alpha _2\in A, \alpha _1\leq \alpha _2})$
be an inverse system of
$ ((X_\alpha )_{\alpha \in A}, (\pi _{\alpha _1,\alpha _2})_{\alpha _1,\alpha _2\in A, \alpha _1\leq \alpha _2})$
be an inverse system of
![]() $\mathbf {PrbAlg}_\Gamma $
-spaces with inverse limit
$\mathbf {PrbAlg}_\Gamma $
-spaces with inverse limit
![]() $(X , (\pi _\alpha )_{\alpha \in A})$
. Further, assume that for all
$(X , (\pi _\alpha )_{\alpha \in A})$
. Further, assume that for all
![]() $\alpha _1,\alpha _2\kern1.4pt{\in}\kern1.4pt A$
with
$\alpha _1,\alpha _2\kern1.4pt{\in}\kern1.4pt A$
with
![]() $\alpha _1\kern1.4pt{<}\kern1.4pt\alpha _2$
, the
$\alpha _1\kern1.4pt{<}\kern1.4pt\alpha _2$
, the
![]() $ \mathbf {PrbAlg}_\Gamma $
-morphism
$ \mathbf {PrbAlg}_\Gamma $
-morphism
![]() $\pi _{\alpha _1,\alpha _2}$
is relatively V-sated. Then the inverse limit
$\pi _{\alpha _1,\alpha _2}$
is relatively V-sated. Then the inverse limit
![]() $X $
is V-sated.
$X $
is V-sated.
Proof. Each
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism
$\mathbf {PrbAlg}_\Gamma $
-morphism
![]() $\pi _\alpha :X \rightarrow X _\alpha $
is relatively V-sated because we can factorize
$\pi _\alpha :X \rightarrow X _\alpha $
is relatively V-sated because we can factorize
![]() $\pi _\alpha =\pi _{\alpha , \alpha ^{\prime }}\circ \pi _{\alpha ^{\prime }}$
for some
$\pi _\alpha =\pi _{\alpha , \alpha ^{\prime }}\circ \pi _{\alpha ^{\prime }}$
for some
![]() $\alpha <\alpha ^{\prime }$
and apply Lemma 4.4. Let
$\alpha <\alpha ^{\prime }$
and apply Lemma 4.4. Let
![]() $\psi :Y\rightarrow X $
be an arbitrary further
$\psi :Y\rightarrow X $
be an arbitrary further
![]() $\mathbf {PrbAlg}_\Gamma $
-morphism. For any
$\mathbf {PrbAlg}_\Gamma $
-morphism. For any
![]() $g\in V(Y) $
and
$g\in V(Y) $
and
![]() $f\in \bigcup _{\alpha \in A} \pi _\alpha ^{*}(L^2(X _\alpha ))$
, we have
$f\in \bigcup _{\alpha \in A} \pi _\alpha ^{*}(L^2(X _\alpha ))$
, we have
Since
![]() $\bigcup _{\alpha \in A} \pi _\alpha ^{*}(L^2(X _\alpha ))$
is dense in
$\bigcup _{\alpha \in A} \pi _\alpha ^{*}(L^2(X _\alpha ))$
is dense in
![]() $ L^2(X )$
, f in the last equation can be replaced by any function in
$ L^2(X )$
, f in the last equation can be replaced by any function in
![]() $L^2(X )$
. Thus,
$L^2(X )$
. Thus,
![]() $V(Y)$
and
$V(Y)$
and
![]() $\psi ^{*}(L^2(X ))$
are relatively orthogonal over
$\psi ^{*}(L^2(X ))$
are relatively orthogonal over
![]() $ \psi ^{*}(V(X ))$
, and so
$ \psi ^{*}(V(X ))$
, and so
![]() $X $
is V-sated.
$X $
is V-sated.
Lemma 4.6. Every
![]() $\mathbf {PrbAlg}_\Gamma $
-space
$\mathbf {PrbAlg}_\Gamma $
-space
![]() $X $
has a relatively V-sated extension.
$X $
has a relatively V-sated extension.

Figure 2 The subspace relations in Lemma 4.4.
Proof. We write all elements of
![]() $L^2(X )$
as
$L^2(X )$
as
![]() $\{f_{\beta ^{\prime }}\}_{\beta ^{\prime }<\alpha ^{\prime }}$
for some limit ordinal number
$\{f_{\beta ^{\prime }}\}_{\beta ^{\prime }<\alpha ^{\prime }}$
for some limit ordinal number
![]() $ \alpha ^{\prime }$
. For each ordinal
$ \alpha ^{\prime }$
. For each ordinal
![]() $\gamma <\alpha ^{\prime }$
, we let
$\gamma <\alpha ^{\prime }$
, we let
![]() $ A_\gamma =\{f_{\beta ^{\prime }}: \beta ^{\prime }\leq \gamma \}$
. Define a well ordering on the set
$ A_\gamma =\{f_{\beta ^{\prime }}: \beta ^{\prime }\leq \gamma \}$
. Define a well ordering on the set
![]() $\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
by the relation
$\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
by the relation
Since
![]() $\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
is well ordered, there exists an ordinal
$\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
is well ordered, there exists an ordinal
![]() $\alpha $
and an order-preserving bijection
$\alpha $
and an order-preserving bijection
![]() $ \Psi $
from
$ \Psi $
from
![]() $\{\beta : \beta <\alpha \}$
to
$\{\beta : \beta <\alpha \}$
to
![]() $\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
. Since
$\bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
. Since
![]() $\alpha ^{\prime }$
is a limit ordinal, for each
$\alpha ^{\prime }$
is a limit ordinal, for each
![]() $\gamma <\alpha ^{\prime }$
, there is some
$\gamma <\alpha ^{\prime }$
, there is some
![]() $\gamma <\gamma ^{\prime }<\alpha ^{\prime }$
. As a result, there is no maximal element in
$\gamma <\gamma ^{\prime }<\alpha ^{\prime }$
. As a result, there is no maximal element in
![]() $ \bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
; in other words,
$ \bigcup _{\gamma <\alpha ^{\prime }} \{\gamma \}\times A_\gamma $
; in other words,
![]() $\alpha $
is a limit ordinal as well.
$\alpha $
is a limit ordinal as well.
Let
![]() $\Phi =\Pi \circ \Psi $
, where
$\Phi =\Pi \circ \Psi $
, where
![]() $\Pi $
is the projection mapping to the second coordinate. For each
$\Pi $
is the projection mapping to the second coordinate. For each
![]() $\gamma <\alpha $
and
$\gamma <\alpha $
and
![]() $f_{\beta ^{\prime }}\in L^2(X )$
, we claim that there exists
$f_{\beta ^{\prime }}\in L^2(X )$
, we claim that there exists
![]() $\tau>\gamma $
such that
$\tau>\gamma $
such that
![]() $\Phi (\tau )=f_{\beta ^{ \prime }}$
. Suppose
$\Phi (\tau )=f_{\beta ^{ \prime }}$
. Suppose
![]() $\Psi (\gamma )=(\beta , g)$
. We let
$\Psi (\gamma )=(\beta , g)$
. We let
![]() $\beta _{\max }:=\max \{ \beta ,\beta ^{\prime }\}+1<\alpha ^{\prime }$
and then
$\beta _{\max }:=\max \{ \beta ,\beta ^{\prime }\}+1<\alpha ^{\prime }$
and then
![]() $\Psi ^{-1}(\beta _{ \max },f_{\beta ^{\prime }})$
is the desired
$\Psi ^{-1}(\beta _{ \max },f_{\beta ^{\prime }})$
is the desired
![]() $\tau $
. The interpretation is, when enumerating
$\tau $
. The interpretation is, when enumerating
![]() $L^2(X )$
by
$L^2(X )$
by
![]() $\Phi $
, each function appears not only infinitely many times, but also arbitrarily late.
$\Phi $
, each function appears not only infinitely many times, but also arbitrarily late.
Resorting to transfinite induction, we construct a
![]() $\mathbf {PrbAlg}_\Gamma $
-extension
$\mathbf {PrbAlg}_\Gamma $
-extension
![]() $X _\beta $
of
$X _\beta $
of
![]() $X $
for every
$X $
for every
![]() $\beta <\alpha $
and a
$\beta <\alpha $
and a
![]() $\mathbf {PrbAlg} _\Gamma $
-morphism
$\mathbf {PrbAlg} _\Gamma $
-morphism
![]() $\phi _\gamma ^\beta $
from
$\phi _\gamma ^\beta $
from
![]() $X _\beta $
to
$X _\beta $
to
![]() $X _\gamma $
for every
$X _\gamma $
for every
![]() $\gamma <\beta <\alpha $
. Set
$\gamma <\beta <\alpha $
. Set
![]() $X _\emptyset :=X $
. Suppose
$X _\emptyset :=X $
. Suppose
![]() $\epsilon \leq \alpha $
is an ordinal and for each
$\epsilon \leq \alpha $
is an ordinal and for each
![]() $\gamma <\beta <\epsilon $
,
$\gamma <\beta <\epsilon $
,
![]() $X _\beta $
and
$X _\beta $
and
![]() $ \phi _\gamma ^\beta $
have been constructed.
$ \phi _\gamma ^\beta $
have been constructed.
Case 1:
![]() $\epsilon $
is the successor of
$\epsilon $
is the successor of
![]() $\epsilon -1$
. For any
$\epsilon -1$
. For any
![]() $\mathbf {PrbAlg} _\Gamma $
-extension
$\mathbf {PrbAlg} _\Gamma $
-extension
![]() $\eta :Z\to X _{\epsilon -1}$
, we have
$\eta :Z\to X _{\epsilon -1}$
, we have
 $$ \begin{align*} &\|P_{V(Z)}((\phi_\emptyset^{\epsilon-1}\circ \eta)^{*}\Phi(\epsilon))\|_2 - \|P_{V(X _{\epsilon-1})}((\phi_\emptyset^{\epsilon-1})^{*}\Phi(\epsilon))\|_2\\ &\quad \leq \|\Phi(\epsilon)\|_2 - \|P_{V(X_{\epsilon-1})}((\phi_\emptyset^{\epsilon-1})^{*}\Phi(\epsilon))\|_2 \end{align*} $$
$$ \begin{align*} &\|P_{V(Z)}((\phi_\emptyset^{\epsilon-1}\circ \eta)^{*}\Phi(\epsilon))\|_2 - \|P_{V(X _{\epsilon-1})}((\phi_\emptyset^{\epsilon-1})^{*}\Phi(\epsilon))\|_2\\ &\quad \leq \|\Phi(\epsilon)\|_2 - \|P_{V(X_{\epsilon-1})}((\phi_\emptyset^{\epsilon-1})^{*}\Phi(\epsilon))\|_2 \end{align*} $$
since every orthogonal projection is a contraction. Hence, we find a
![]() $ \mathbf {PrbAlg}_\Gamma $
-extension
$ \mathbf {PrbAlg}_\Gamma $
-extension
![]() $\phi ^{\epsilon }_{\epsilon -1}:X _\epsilon \rightarrow X _{\epsilon -1}$
such that the difference
$\phi ^{\epsilon }_{\epsilon -1}:X _\epsilon \rightarrow X _{\epsilon -1}$
such that the difference
is at least half its supremum value over all extensions
![]() $\eta :Z\to X _{\epsilon -1}$
. For any
$\eta :Z\to X _{\epsilon -1}$
. For any
![]() $\gamma <\epsilon -1$
, we set
$\gamma <\epsilon -1$
, we set
![]() $\phi _\gamma ^\epsilon := \phi _\gamma ^{\epsilon -1}\circ \phi ^{\epsilon }_{\epsilon -1}$
.
$\phi _\gamma ^\epsilon := \phi _\gamma ^{\epsilon -1}\circ \phi ^{\epsilon }_{\epsilon -1}$
.
Case 2:
![]() $\epsilon $
is a limit ordinal. Let
$\epsilon $
is a limit ordinal. Let
![]() $(Z_\epsilon ,(\psi _\beta ^ \epsilon )_{\beta <\epsilon })$
be the inverse limit of the inverse system
$(Z_\epsilon ,(\psi _\beta ^ \epsilon )_{\beta <\epsilon })$
be the inverse limit of the inverse system
![]() $((X _\beta )_{\beta <\epsilon },(\phi _{\gamma }^ \beta )_{\gamma \leq \beta <\epsilon })$
. Let
$((X _\beta )_{\beta <\epsilon },(\phi _{\gamma }^ \beta )_{\gamma \leq \beta <\epsilon })$
. Let
![]() $\psi _{\epsilon }:X _\epsilon \rightarrow Z_{\epsilon }$
be a
$\psi _{\epsilon }:X _\epsilon \rightarrow Z_{\epsilon }$
be a
![]() $\mathbf {PrbAlg}_\Gamma $
-extension such that the difference
$\mathbf {PrbAlg}_\Gamma $
-extension such that the difference
is at least half its supremum possible value over all extensions of
![]() $ Z_{\epsilon }$
. Set
$ Z_{\epsilon }$
. Set
![]() $\phi _\gamma ^\epsilon :=\psi _\gamma ^{\epsilon }\circ \psi _{\epsilon }$
.
$\phi _\gamma ^\epsilon :=\psi _\gamma ^{\epsilon }\circ \psi _{\epsilon }$
.
We now show that
![]() $\phi _\emptyset ^\alpha :X _\alpha \rightarrow X $
is relatively V-sated. Let
$\phi _\emptyset ^\alpha :X _\alpha \rightarrow X $
is relatively V-sated. Let
![]() $\pi :Y\rightarrow X _\alpha $
be an arbitrary further extension. By Lemma 4.2, it is equivalent to showing that for any
$\pi :Y\rightarrow X _\alpha $
be an arbitrary further extension. By Lemma 4.2, it is equivalent to showing that for any
![]() $f\in L^2(X )$
,
$f\in L^2(X )$
,
Since
![]() $\pi ^{*}(V(X _\alpha ))\subset V(Y)$
, it suffices to show
$\pi ^{*}(V(X _\alpha ))\subset V(Y)$
, it suffices to show
Suppose for contradiction,
![]() $\|P_{V(Y)}((\phi _\emptyset ^\alpha \circ \pi )^{*}f)\|_2> \|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f) \|_2$
. We know
$\|P_{V(Y)}((\phi _\emptyset ^\alpha \circ \pi )^{*}f)\|_2> \|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f) \|_2$
. We know
![]() $ \|P_{V(X _\gamma )}((\phi _\emptyset ^\gamma )^{*}f) \|_2$
is increasing in
$ \|P_{V(X _\gamma )}((\phi _\emptyset ^\gamma )^{*}f) \|_2$
is increasing in
![]() $ \gamma $
and bounded above by
$ \gamma $
and bounded above by
![]() $\|f\|_2$
. By the construction of
$\|f\|_2$
. By the construction of
![]() $\Phi $
, f appears in the image of
$\Phi $
, f appears in the image of
![]() $\Phi $
infinitely many times. There exists an ordinal
$\Phi $
infinitely many times. There exists an ordinal
![]() $\gamma $
large enough such that
$\gamma $
large enough such that
![]() $\Phi (\gamma )=f$
and one of the following holds:
$\Phi (\gamma )=f$
and one of the following holds:
-
(i)
 $\gamma $
is a successor and
$\gamma $
is a successor and  $$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(X_{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2\\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2 - \|P_{V(X_\alpha)}((\phi_\emptyset^\alpha)^{*}f)\|_2 ); \end{align*} $$
$$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(X_{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2\\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2 - \|P_{V(X_\alpha)}((\phi_\emptyset^\alpha)^{*}f)\|_2 ); \end{align*} $$
-
(ii)
 $\gamma $
is a limit ordinal and
$\gamma $
is a limit ordinal and  $$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f) \|_2\\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2- \|P_{V(X _\alpha)}((\phi_\emptyset^\alpha)^{*}f) \|_2 ). \end{align*} $$
$$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f) \|_2\\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2- \|P_{V(X _\alpha)}((\phi_\emptyset^\alpha)^{*}f) \|_2 ). \end{align*} $$
Since
![]() $\|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f)\|_2\geq \|P_{V(X _{\gamma -1})}((\phi _\emptyset ^{\gamma -1})^{*}f) \|_2$
when
$\|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f)\|_2\geq \|P_{V(X _{\gamma -1})}((\phi _\emptyset ^{\gamma -1})^{*}f) \|_2$
when
![]() $\gamma $
is a successor and
$\gamma $
is a successor and
![]() $\|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f) \|_2\geq \|P_{V(Z_{\gamma })}((\psi _\emptyset ^{\gamma })^{*}f)\|_2$
when
$\|P_{V(X _\alpha )}((\phi _\emptyset ^\alpha )^{*}f) \|_2\geq \|P_{V(Z_{\gamma })}((\psi _\emptyset ^{\gamma })^{*}f)\|_2$
when
![]() $\gamma $
is a limit ordinal, we have
$\gamma $
is a limit ordinal, we have
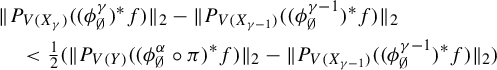 $$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(X _{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2 \\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}(( \phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2 - \|P_{V(X _{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2 ) \end{align*} $$
$$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(X _{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2 \\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}(( \phi_\emptyset^\alpha\circ \pi)^{*}f)\|_2 - \|P_{V(X _{\gamma-1})}((\phi_\emptyset^{\gamma-1})^{*}f) \|_2 ) \end{align*} $$
or
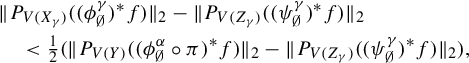 $$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f) \|_2 \\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f )\|_2 - \|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f)\|_2 ), \end{align*} $$
$$ \begin{align*} &\|P_{V(X _\gamma)}((\phi_\emptyset^\gamma)^{*}f) \|_2-\|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f) \|_2 \\ &\quad <\tfrac{1}{2} (\|P_{V(Y)}((\phi_\emptyset^\alpha\circ \pi)^{*}f )\|_2 - \|P_{V(Z_{\gamma})}((\psi_\emptyset^{\gamma})^{*}f)\|_2 ), \end{align*} $$
either of which contradicts our choice of
![]() $X _\gamma $
. Thus, we have
$X _\gamma $
. Thus, we have
![]() $ \phi _\emptyset ^\alpha :X _\alpha \rightarrow X $
is relatively V-sated.
$ \phi _\emptyset ^\alpha :X _\alpha \rightarrow X $
is relatively V-sated.
Lemmas 4.5 and 4.6 give the following theorem.
Theorem 4.7. If V is a functorial
![]() $L^2$
-subspace of
$L^2$
-subspace of
![]() $\mathbf {PrbAlg}_\Gamma $
-spaces, then for every
$\mathbf {PrbAlg}_\Gamma $
-spaces, then for every
![]() $\mathbf {PrbAlg}_\Gamma $
-space
$\mathbf {PrbAlg}_\Gamma $
-space
![]() $X=(X,\mu )$
, there is a
$X=(X,\mu )$
, there is a
![]() $ \mathbf {PrbAlg}_\Gamma $
-morphism
$ \mathbf {PrbAlg}_\Gamma $
-morphism
![]() $\pi :Y\rightarrow X $
such that
$\pi :Y\rightarrow X $
such that
![]() $Y=(Y,\nu )$
is V-sated.
$Y=(Y,\nu )$
is V-sated.
4.2 Extending factors relative to subgroups
In this section, we show how to extend a factor map relative to a subgroup to a factor map of the whole group. The corresponding result for countable groups and standard Lebesgue spaces is [Reference Austin2, Theorem 2.1].
Theorem 4.8. Let
![]() $\Gamma $
be an arbitrary discrete group, not necessarily countable or amenable. Let H be a subgroup of
$\Gamma $
be an arbitrary discrete group, not necessarily countable or amenable. Let H be a subgroup of
![]() $\Gamma $
. Let
$\Gamma $
. Let
![]() $X=(X,\mu ,T)$
be a
$X=(X,\mu ,T)$
be a
![]() $\mathbf {PrbAlg}_\Gamma $
-system and
$\mathbf {PrbAlg}_\Gamma $
-system and
![]() $Y=(Y,\nu ,S)$
a
$Y=(Y,\nu ,S)$
a
![]() $\mathbf {PrbAlg}_H$
-system. Denote by
$\mathbf {PrbAlg}_H$
-system. Denote by
![]() $X_H=(X,\mu ,T|_H)$
the
$X_H=(X,\mu ,T|_H)$
the
![]() $\mathbf {PrbAlg}_H$
-system, where
$\mathbf {PrbAlg}_H$
-system, where
![]() $ T|_H$
is the restriction of the group homomorphism
$ T|_H$
is the restriction of the group homomorphism
![]() $T:\Gamma \to \mathrm {Aut} (X,\mu )$
to H. If
$T:\Gamma \to \mathrm {Aut} (X,\mu )$
to H. If
![]() $\beta :Y\to X_H$
is a
$\beta :Y\to X_H$
is a
![]() $\mathbf {PrbAlg}_H$
-morphism, then there are a
$\mathbf {PrbAlg}_H$
-morphism, then there are a
![]() $\mathbf {PrbAlg}_\Gamma $
-system
$\mathbf {PrbAlg}_\Gamma $
-system
![]() $Z=(Z,\theta ,R)$
, a
$Z=(Z,\theta ,R)$
, a
![]() $\mathbf{PrbAlg}_\Gamma $
-extension
$\mathbf{PrbAlg}_\Gamma $
-extension
![]() $\pi :Z\to X$
, and a
$\pi :Z\to X$
, and a
![]() $\mathbf {PrbAlg}_H$
-extension
$\mathbf {PrbAlg}_H$
-extension
![]() $ \alpha :Z_H\to Y$
such that the diagram
$ \alpha :Z_H\to Y$
such that the diagram
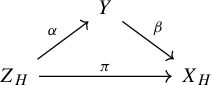
commutes in
![]() $\mathbf {PrbAlg}_H$
.
$\mathbf {PrbAlg}_H$
.
Proof. We pass to the canonical models
![]() $\tilde {X}=(\tilde {X},\mathcal {B}a(\tilde {X}),\tilde {\mu }, \tilde {T})$
,
$\tilde {X}=(\tilde {X},\mathcal {B}a(\tilde {X}),\tilde {\mu }, \tilde {T})$
,
![]() $\tilde {Y}=(\tilde {Y},\mathcal {B}a(\tilde {Y}),\tilde {\nu }, \tilde {S})$
, and
$\tilde {Y}=(\tilde {Y},\mathcal {B}a(\tilde {Y}),\tilde {\nu }, \tilde {S})$
, and
![]() $\tilde {\beta }$
of X, Y, and
$\tilde {\beta }$
of X, Y, and
![]() $\beta $
, respectively. We construct Z,
$\beta $
, respectively. We construct Z,
![]() $\alpha $
, and
$\alpha $
, and
![]() $\pi $
as follows. First, we construct a
$\pi $
as follows. First, we construct a
![]() ${\mathbf {CH}}_\Gamma $
-system
${\mathbf {CH}}_\Gamma $
-system
![]() $(\tilde {Z},\tilde {R})$
, and
$(\tilde {Z},\tilde {R})$
, and
![]() ${\mathbf {CH}}_\Gamma $
-maps
${\mathbf {CH}}_\Gamma $
-maps
![]() $\tilde {\alpha }$
and
$\tilde {\alpha }$
and
![]() $\tilde {\pi }$
satisfying a related commutative diagram in the dynamical category
$\tilde {\pi }$
satisfying a related commutative diagram in the dynamical category
![]() ${\mathbf{CH}}_\Gamma $
. (We denote by
${\mathbf{CH}}_\Gamma $
. (We denote by
![]() $\mathbf {CH}$
the category of compact Hausdorff spaces and continuous maps, and
$\mathbf {CH}$
the category of compact Hausdorff spaces and continuous maps, and
![]() ${\mathbf {CH}}_\Gamma $
denotes the category of topological dynamical
${\mathbf {CH}}_\Gamma $
denotes the category of topological dynamical
![]() $\Gamma $
-systems formed on compact Hausdorff spaces and continuous factor maps, where the
$\Gamma $
-systems formed on compact Hausdorff spaces and continuous factor maps, where the
![]() $\Gamma $
-action is given by homeomorphisms) Second, we construct a probability measure
$\Gamma $
-action is given by homeomorphisms) Second, we construct a probability measure
![]() $\tilde \theta $
on
$\tilde \theta $
on
![]() $ (\tilde Z,\mathcal {B}a(\tilde {Z}))$
and show that it preserves the
$ (\tilde Z,\mathcal {B}a(\tilde {Z}))$
and show that it preserves the
![]() $\tilde {R} $
-action. Finally, we verify that this
$\tilde {R} $
-action. Finally, we verify that this
![]() ${\mathbf {CHPrb}_{\Gamma }}$
-system satisfies the right commutative diagram. We can then map this diagram to the dynamical categories of probability algebras using the deletion and abstraction functors
${\mathbf {CHPrb}_{\Gamma }}$
-system satisfies the right commutative diagram. We can then map this diagram to the dynamical categories of probability algebras using the deletion and abstraction functors
![]() $\texttt {Alg}$
and
$\texttt {Alg}$
and
![]() $\texttt {Abs}$
.
$\texttt {Abs}$
.
Step 1: we build a
![]() ${\mathbf {CH}}_\Gamma $
-system
${\mathbf {CH}}_\Gamma $
-system
![]() $(\tilde {Z},\tilde {R})$
. Let
$(\tilde {Z},\tilde {R})$
. Let
where e is the identity of
![]() $\Gamma $
. Note that
$\Gamma $
. Note that
![]() $\tilde {Z}$
is a compact subspace of
$\tilde {Z}$
is a compact subspace of
![]() $\tilde {Y}^\Gamma $
(this basically follows from the fact that
$\tilde {Y}^\Gamma $
(this basically follows from the fact that
![]() $ \tilde {S},\tilde {T}$
act by homeomorphisms and
$ \tilde {S},\tilde {T}$
act by homeomorphisms and
![]() $\tilde {\beta }$
is continuous). We can define a
$\tilde {\beta }$
is continuous). We can define a
![]() ${\mathbf {CH}}_\Gamma $
-action
${\mathbf {CH}}_\Gamma $
-action
![]() $\tilde {R} :\Gamma \to \mathrm {Aut}(\tilde {Z})$
by
$\tilde {R} :\Gamma \to \mathrm {Aut}(\tilde {Z})$
by
(One easily checks that
![]() $\tilde {Z}$
is an
$\tilde {Z}$
is an
![]() $\tilde R$
-invariant set so that
$\tilde R$
-invariant set so that
![]() $ \tilde R$
is well defined).
$ \tilde R$
is well defined).
We set
![]() $\tilde {\alpha } : \tilde {Z}\rightarrow \tilde {Y}$
to be
$\tilde {\alpha } : \tilde {Z}\rightarrow \tilde {Y}$
to be
![]() $\tilde {\alpha }((y_\gamma )_{\gamma \in \Gamma }) := y_e$
and
$\tilde {\alpha }((y_\gamma )_{\gamma \in \Gamma }) := y_e$
and
![]() $\tilde {\pi }:=\tilde {\beta } \circ \tilde {\alpha }$
. By construction, the diagram
$\tilde {\pi }:=\tilde {\beta } \circ \tilde {\alpha }$
. By construction, the diagram
commutes in the dynamical category
![]() ${\mathbf {CH}}_H$
. By construction of
${\mathbf {CH}}_H$
. By construction of
![]() $ \tilde {Z}$
, the map
$ \tilde {Z}$
, the map
![]() $\tilde {\pi }$
is also a
$\tilde {\pi }$
is also a
![]() ${\mathbf {CH}}_\Gamma $
-factor map.
${\mathbf {CH}}_\Gamma $
-factor map.
Endow the space
![]() $\tilde {Z}$
with the Baire
$\tilde {Z}$
with the Baire
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}a( \tilde {Z})$
, which coincides with the restriction of
$\mathcal {B}a( \tilde {Z})$
, which coincides with the restriction of
![]() $\mathcal {B}a(\tilde {Y} ^\Gamma )=\mathcal {B}a(\tilde {Y})^{\otimes \Gamma }$
to
$\mathcal {B}a(\tilde {Y} ^\Gamma )=\mathcal {B}a(\tilde {Y})^{\otimes \Gamma }$
to
![]() $\tilde {Z}$
by [Reference Jamneshan and Tao21, Lemma 2.1]. In particular, the maps in the previous diagram preserve Baire measurability.
$\tilde {Z}$
by [Reference Jamneshan and Tao21, Lemma 2.1]. In particular, the maps in the previous diagram preserve Baire measurability.
Step 2: we construct a probability measure
![]() $\tilde {\theta }$
on
$\tilde {\theta }$
on
![]() $(\tilde {Z}, \mathcal {B}a(\tilde {Z}))$
. Let
$(\tilde {Z}, \mathcal {B}a(\tilde {Z}))$
. Let
![]() $\{\nu _x\}_{x\in \tilde {X}}$
be the canonical disintegration (see Theorem 2.2) of
$\{\nu _x\}_{x\in \tilde {X}}$
be the canonical disintegration (see Theorem 2.2) of
![]() $\tilde {\nu }$
with respect to the factor map
$\tilde {\nu }$
with respect to the factor map
![]() $\tilde {\beta } :\tilde {Y}\rightarrow \tilde {X}$
. For each
$\tilde {\beta } :\tilde {Y}\rightarrow \tilde {X}$
. For each
![]() $\gamma \in \Gamma $
and
$\gamma \in \Gamma $
and
![]() $x\in \tilde {X}$
, define
$x\in \tilde {X}$
, define
![]() $\tilde {\nu }_{\gamma ,x}$
on
$\tilde {\nu }_{\gamma ,x}$
on
![]() $(\tilde {Y}^{\gamma H}, \mathcal {B}a(\tilde {Y}^{\gamma H}))$
by
$(\tilde {Y}^{\gamma H}, \mathcal {B}a(\tilde {Y}^{\gamma H}))$
by
Since we can identify the Baire
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}a(\tilde {Y} ^{\gamma H})$
with the product
$\mathcal {B}a(\tilde {Y} ^{\gamma H})$
with the product
![]() $\sigma $
-algebra
$\sigma $
-algebra
![]() $\mathcal {B}a(\tilde {Y} )^{\otimes \gamma H}$
, it follows that
$\mathcal {B}a(\tilde {Y} )^{\otimes \gamma H}$
, it follows that
![]() $\tilde {\nu }_{\gamma ,x}$
is well defined by first verifying cylinder sets and then applying the
$\tilde {\nu }_{\gamma ,x}$
is well defined by first verifying cylinder sets and then applying the
![]() $\pi $
-
$\pi $
-
![]() $ \unicode{x3bb} $
theorem.
$ \unicode{x3bb} $
theorem.
By the axiom of choice, we pick a representative from each left coset
![]() $ \gamma H$
an element
$ \gamma H$
an element
![]() $\omega $
and denote their collection by
$\omega $
and denote their collection by
![]() $\Omega $
. We identify
$\Omega $
. We identify
![]() $\tilde {Y}^{\Gamma }=\Pi _{\omega \in \Omega }\tilde {Y}^{\omega H}$
so as to define a probability measure
$\tilde {Y}^{\Gamma }=\Pi _{\omega \in \Omega }\tilde {Y}^{\omega H}$
so as to define a probability measure
on
![]() $\mathcal {B}a(\tilde {Y}^\Gamma )=\mathcal {B}a(\tilde {Y}^H)^{\otimes \Omega } $
. We show that the definition of
$\mathcal {B}a(\tilde {Y}^\Gamma )=\mathcal {B}a(\tilde {Y}^H)^{\otimes \Omega } $
. We show that the definition of
![]() $\tilde {\nu }_x^{\prime }$
is independent from the choice of representatives. If
$\tilde {\nu }_x^{\prime }$
is independent from the choice of representatives. If
![]() $x\in X$
,
$x\in X$
,
![]() $A\in \mathcal {B }a(\tilde {Y}^{\gamma H})$
, and
$A\in \mathcal {B }a(\tilde {Y}^{\gamma H})$
, and
![]() $\gamma _1=\gamma _2\eta _1$
for some
$\gamma _1=\gamma _2\eta _1$
for some
![]() $\gamma _1,\gamma _2\in \Gamma $
and
$\gamma _1,\gamma _2\in \Gamma $
and
![]() $\eta _1\in H$
, which means
$\eta _1\in H$
, which means
![]() $ \gamma _1H=\gamma _2H$
, then we have
$ \gamma _1H=\gamma _2H$
, then we have
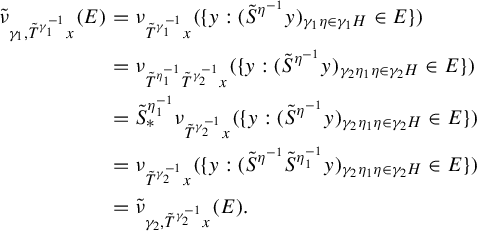 $$ \begin{align*} \begin{split} \tilde{\nu}_{\gamma_1,\tilde{T}^{\gamma_1^{-1}}x}(E)&=\nu_{\tilde{T} ^{\gamma_1^{-1}}x}(\{y:(\tilde{S}^{\eta^{-1}}y)_{\gamma_1\eta\in \gamma_1H}\in E \}) \\ &=\nu_{\tilde{T}^{\eta_1^{-1}}\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S} ^{\eta^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\tilde{S}^{\eta^{-1}_1}_{*}\nu_{\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S} ^{\eta^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\nu_{\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S}^{\eta^{-1}}\tilde{S} ^{\eta_1^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\tilde{\nu}_{\gamma_2,\tilde{T}^{\gamma_2^{-1}}x}(E). \end{split} \end{align*} $$
$$ \begin{align*} \begin{split} \tilde{\nu}_{\gamma_1,\tilde{T}^{\gamma_1^{-1}}x}(E)&=\nu_{\tilde{T} ^{\gamma_1^{-1}}x}(\{y:(\tilde{S}^{\eta^{-1}}y)_{\gamma_1\eta\in \gamma_1H}\in E \}) \\ &=\nu_{\tilde{T}^{\eta_1^{-1}}\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S} ^{\eta^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\tilde{S}^{\eta^{-1}_1}_{*}\nu_{\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S} ^{\eta^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\nu_{\tilde{T}^{\gamma_2^{-1}}x}(\{y:(\tilde{S}^{\eta^{-1}}\tilde{S} ^{\eta_1^{-1}}y)_{\gamma_2\eta_1\eta\in \gamma_2 H}\in E \}) \\ &=\tilde{\nu}_{\gamma_2,\tilde{T}^{\gamma_2^{-1}}x}(E). \end{split} \end{align*} $$
Hence, a finite product of the probability measures
![]() $\tilde {\nu } _{\gamma ,\tilde T^{\gamma ^{-1}}x}$
for
$\tilde {\nu } _{\gamma ,\tilde T^{\gamma ^{-1}}x}$
for
![]() $\gamma $
ranging from different left cosets is independent from the choice of representatives. By the uniqueness part of Carathéodory’s extension theorem, we conclude that the product probability measure
$\gamma $
ranging from different left cosets is independent from the choice of representatives. By the uniqueness part of Carathéodory’s extension theorem, we conclude that the product probability measure
![]() $\tilde {\nu }_x^{\prime }$
is independent from the choice of representatives.
$\tilde {\nu }_x^{\prime }$
is independent from the choice of representatives.
Next, we define a measure
![]() $\tilde {\nu }_x$
on
$\tilde {\nu }_x$
on
![]() $(\tilde {Z},\mathcal {B}a(\tilde { Z}))$
by
$(\tilde {Z},\mathcal {B}a(\tilde { Z}))$
by
for each
![]() $E\in \mathcal {B}a(\tilde {Y}^\Gamma )$
. Note that
$E\in \mathcal {B}a(\tilde {Y}^\Gamma )$
. Note that
![]() $\tilde {Z}$
is a closed subset of
$\tilde {Z}$
is a closed subset of
![]() $\tilde {Y}^\Gamma $
, but may not be Baire measurable. Therefore, we need to check the well definedness of
$\tilde {Y}^\Gamma $
, but may not be Baire measurable. Therefore, we need to check the well definedness of
![]() $\tilde {\nu }_x$
. It suffices to show that
$\tilde {\nu }_x$
. It suffices to show that
Since
![]() $\mathcal {B}a(\tilde {Y}^\Gamma )=\mathcal {B}a(\tilde {Y} )^{\otimes \Gamma } $
, E depends on only countably many coordinates. Hence, there exists
$\mathcal {B}a(\tilde {Y}^\Gamma )=\mathcal {B}a(\tilde {Y} )^{\otimes \Gamma } $
, E depends on only countably many coordinates. Hence, there exists
![]() $\{\gamma _i\}_{i=1}^{\infty }$
such that
$\{\gamma _i\}_{i=1}^{\infty }$
such that
![]() $E=E^{\prime }\times \otimes _{\gamma \in \Gamma \backslash \{\gamma _i\}_{i=1}^{\infty }}\tilde {Y}$
, where
$E=E^{\prime }\times \otimes _{\gamma \in \Gamma \backslash \{\gamma _i\}_{i=1}^{\infty }}\tilde {Y}$
, where
![]() $E^{\prime }\in \mathcal {B}a(\tilde {Y})^{\otimes \mathbb {N}}$
. Let
$E^{\prime }\in \mathcal {B}a(\tilde {Y})^{\otimes \mathbb {N}}$
. Let
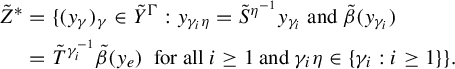 $$ \begin{align*} \tilde{Z}^{*} &=\{(y_\gamma)_\gamma\in \tilde{Y}^\Gamma: y_{\gamma_i\eta}=\tilde{ S}^{\eta^{-1}}y_{\gamma_i} \text{ and }\tilde{\beta}(y_{\gamma_i})\\ &=\tilde{T} ^{\gamma_i^{-1}}\tilde{\beta}(y_e)\; \text{ for all } i\geq 1 \text{ and } \gamma_i\eta\in \{\gamma_i: i\geq 1\}\}. \end{align*} $$
$$ \begin{align*} \tilde{Z}^{*} &=\{(y_\gamma)_\gamma\in \tilde{Y}^\Gamma: y_{\gamma_i\eta}=\tilde{ S}^{\eta^{-1}}y_{\gamma_i} \text{ and }\tilde{\beta}(y_{\gamma_i})\\ &=\tilde{T} ^{\gamma_i^{-1}}\tilde{\beta}(y_e)\; \text{ for all } i\geq 1 \text{ and } \gamma_i\eta\in \{\gamma_i: i\geq 1\}\}. \end{align*} $$
Since
![]() $\tilde {Z}\cap E=\emptyset $
implies
$\tilde {Z}\cap E=\emptyset $
implies
![]() $\tilde {Z}^{*}\cap E=\emptyset $
, to show
$\tilde {Z}^{*}\cap E=\emptyset $
, to show
![]() $\tilde {\nu }^{\prime }_x(E)=0$
, it suffices to show
$\tilde {\nu }^{\prime }_x(E)=0$
, it suffices to show
![]() ${\tilde {\nu }^{\prime }_x(\tilde {Z}^{*})=1}$
(since
${\tilde {\nu }^{\prime }_x(\tilde {Z}^{*})=1}$
(since
![]() $\tilde {Z}^{*}$
only depends on countable many coordinates, it is guaranteed to be Baire measurable). We group the
$\tilde {Z}^{*}$
only depends on countable many coordinates, it is guaranteed to be Baire measurable). We group the
![]() $ \gamma _i$
according to the left cosets
$ \gamma _i$
according to the left cosets
![]() $\omega H$
to which they belong. So suppose
$\omega H$
to which they belong. So suppose
![]() $\{\gamma _i\}=\bigcup _i \{\omega _i\eta _{i,j}\}_j$
, where each
$\{\gamma _i\}=\bigcup _i \{\omega _i\eta _{i,j}\}_j$
, where each
![]() $\eta _{i,j}\in H$
,
$\eta _{i,j}\in H$
,
![]() $\omega _i\in \Omega $
. For each
$\omega _i\in \Omega $
. For each
![]() $\omega _i$
, we have
$\omega _i$
, we have
Note that
Thus,
![]() $\tilde {\nu }_x^{\prime }(\tilde {Z}^{*})=1$
and consequently,
$\tilde {\nu }_x^{\prime }(\tilde {Z}^{*})=1$
and consequently,
![]() $\tilde {\nu } _x$
is well defined.
$\tilde {\nu } _x$
is well defined.
For any set
![]() $A=A^{\prime }\cap \tilde {Z}\in \mathcal {B}a(\tilde {Z})$
where
$A=A^{\prime }\cap \tilde {Z}\in \mathcal {B}a(\tilde {Z})$
where
![]() $ A^{\prime }\in \mathcal {B}a(\tilde {Y}^\Gamma )$
, we aim to prove the mapping
$ A^{\prime }\in \mathcal {B}a(\tilde {Y}^\Gamma )$
, we aim to prove the mapping
![]() $ x\mapsto \tilde {\nu }_x(A)$
is Baire measurable. Suppose there are
$ x\mapsto \tilde {\nu }_x(A)$
is Baire measurable. Suppose there are
![]() $ \omega _1,\ldots ,\omega _m\in \Omega $
,
$ \omega _1,\ldots ,\omega _m\in \Omega $
,
![]() $\eta _{i,1}, \ldots ,\eta _{i,n_i}\in H$
for each
$\eta _{i,1}, \ldots ,\eta _{i,n_i}\in H$
for each
![]() $i\leq m$
, and
$i\leq m$
, and
![]() $A_{i,j}\in \mathcal {B}a(\tilde {Y})$
for all
$A_{i,j}\in \mathcal {B}a(\tilde {Y})$
for all
![]() $i\leq m $
and
$i\leq m $
and
![]() $j\leq n_i$
such that
$j\leq n_i$
such that
![]() $A^{\prime }=\{(y_\gamma )_\gamma :y_{\omega _i\eta _{i,j}}\in A_{i,j} \text { for all } i\leq m, j\leq n_i\}$
. Then
$A^{\prime }=\{(y_\gamma )_\gamma :y_{\omega _i\eta _{i,j}}\in A_{i,j} \text { for all } i\leq m, j\leq n_i\}$
. Then
 $$ \begin{align} \tilde{\nu}_x^{\prime }(A^{\prime })&=\prod_{i=1}^m \tilde{\nu}_{\omega_i, \tilde{T}^{\omega_i^{-1}}x}(\{(y_{\omega_i\eta})_{\eta\in H}:y_{\omega_i\eta_{i,j}}\in A_{i,j} \text{ for any } j\leq n_i \}) \nonumber\\ &=\prod_{i=1}^m \nu_{\tilde{T}^{\omega_i^{-1}}x}(\tilde{S} ^{\eta_{i,1}}(A_{i,1})\cap\cdots\cap \tilde{S}^{\eta_{i,n_i}}(A_{i,n_i})). \end{align} $$
$$ \begin{align} \tilde{\nu}_x^{\prime }(A^{\prime })&=\prod_{i=1}^m \tilde{\nu}_{\omega_i, \tilde{T}^{\omega_i^{-1}}x}(\{(y_{\omega_i\eta})_{\eta\in H}:y_{\omega_i\eta_{i,j}}\in A_{i,j} \text{ for any } j\leq n_i \}) \nonumber\\ &=\prod_{i=1}^m \nu_{\tilde{T}^{\omega_i^{-1}}x}(\tilde{S} ^{\eta_{i,1}}(A_{i,1})\cap\cdots\cap \tilde{S}^{\eta_{i,n_i}}(A_{i,n_i})). \end{align} $$
Since
![]() $x\mapsto \nu _x$
is Baire measurable and the product of finitely many Baire measurable functions is still Baire measurable, it follows that
$x\mapsto \nu _x$
is Baire measurable and the product of finitely many Baire measurable functions is still Baire measurable, it follows that
![]() $ x\mapsto \tilde {\nu }_x(A)$
is Baire measurable whenever
$ x\mapsto \tilde {\nu }_x(A)$
is Baire measurable whenever
![]() $A^{\prime }\in \mathcal {B}a(\tilde {Y}^\Gamma )$
, as the cylinder sets generate
$A^{\prime }\in \mathcal {B}a(\tilde {Y}^\Gamma )$
, as the cylinder sets generate
![]() $\mathcal {B}a( \tilde {Y}^\Gamma )$
. As a result, we are able to define
$\mathcal {B}a( \tilde {Y}^\Gamma )$
. As a result, we are able to define
Observe that each
![]() $\tilde {\nu }_x(\tilde {Z})=\tilde {\nu }_x^{\prime }(\tilde {Y} ^{\Gamma })=1$
. Therefore,
$\tilde {\nu }_x(\tilde {Z})=\tilde {\nu }_x^{\prime }(\tilde {Y} ^{\Gamma })=1$
. Therefore,
![]() $\tilde {\theta }$
is a probability measure as well.
$\tilde {\theta }$
is a probability measure as well.
Step 3: we verify that
![]() $(\tilde {Z},\mathcal {B}a(\tilde {Z}),\tilde {\theta }, \tilde {R})$
is a
$(\tilde {Z},\mathcal {B}a(\tilde {Z}),\tilde {\theta }, \tilde {R})$
is a
![]() ${\mathbf {CHPrb}_{\Gamma }}$
-system satisfying the desired diagram.
${\mathbf {CHPrb}_{\Gamma }}$
-system satisfying the desired diagram.
We claim that
![]() $\tilde {R}$
is a measure-preserving transformation. Suppose
$\tilde {R}$
is a measure-preserving transformation. Suppose
![]() $ \gamma ^{\prime }\in \Gamma $
,
$ \gamma ^{\prime }\in \Gamma $
,
![]() $x\in \tilde X$
,
$x\in \tilde X$
,
![]() $\omega _1,\ldots ,\omega _m\in \Omega $
,
$\omega _1,\ldots ,\omega _m\in \Omega $
,
![]() $\eta _{i,1},\ldots ,\eta _{i,n_i}\in H$
for each
$\eta _{i,1},\ldots ,\eta _{i,n_i}\in H$
for each
![]() $i\leq m$
, and
$i\leq m$
, and
![]() $ A_{i,j}\in \mathcal {B}a(\tilde {Y})$
for all
$ A_{i,j}\in \mathcal {B}a(\tilde {Y})$
for all
![]() $i\leq m$
and
$i\leq m$
and
![]() $j\leq n_i$
. Then we obtain
$j\leq n_i$
. Then we obtain
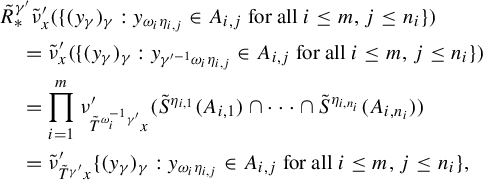 $$ \begin{align*} & \tilde{R}_{*}^{\gamma^{\prime }} \tilde{\nu}_x^{\prime }(\{(y_\gamma)_\gamma: y_{\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}) \\ &\quad = \tilde{\nu}_x^{\prime }(\{(y_\gamma)_\gamma: y_{\gamma^{\prime -1}\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}) \\ &\quad = \prod_{i=1}^m \nu_{\tilde{T}^{\omega_i^{-1}\gamma^{\prime }}x}^{\prime }( \tilde{S}^{\eta_{i,1}}(A_{i,1})\cap\cdots \cap \tilde{S}^{ \eta_{i,n_i}}(A_{i,n_i})) \\ &\quad = \tilde{\nu}_{\tilde{T}^{\gamma^{\prime }} x}^{\prime }\{(y_\gamma)_\gamma: y_{\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}, \end{align*} $$
$$ \begin{align*} & \tilde{R}_{*}^{\gamma^{\prime }} \tilde{\nu}_x^{\prime }(\{(y_\gamma)_\gamma: y_{\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}) \\ &\quad = \tilde{\nu}_x^{\prime }(\{(y_\gamma)_\gamma: y_{\gamma^{\prime -1}\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}) \\ &\quad = \prod_{i=1}^m \nu_{\tilde{T}^{\omega_i^{-1}\gamma^{\prime }}x}^{\prime }( \tilde{S}^{\eta_{i,1}}(A_{i,1})\cap\cdots \cap \tilde{S}^{ \eta_{i,n_i}}(A_{i,n_i})) \\ &\quad = \tilde{\nu}_{\tilde{T}^{\gamma^{\prime }} x}^{\prime }\{(y_\gamma)_\gamma: y_{\omega_i\eta_{i,j}}\in A_{i,j}\text{ for all } i\leq m, j\leq n_i\}, \end{align*} $$
where the last two equalities follow from two applications of equation (8) (while in the first applications, we work with a family of representatives
![]() $\gamma ^{\prime -1}\Omega $
instead of
$\gamma ^{\prime -1}\Omega $
instead of
![]() $\Omega $
). Therefore,
$\Omega $
). Therefore,
![]() $\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x^{\prime }=\tilde { \nu }_{\tilde {T}^{\gamma ^{\prime }}x}^{\prime }$
. By the definition of
$\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x^{\prime }=\tilde { \nu }_{\tilde {T}^{\gamma ^{\prime }}x}^{\prime }$
. By the definition of
![]() $ \tilde {\nu }_x$
,
$ \tilde {\nu }_x$
,
![]() $\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x=\tilde {\nu }_{ \tilde {T}^{\gamma ^{\prime }}x}$
. Since
$\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x=\tilde {\nu }_{ \tilde {T}^{\gamma ^{\prime }}x}$
. Since
![]() $\tilde {\mu }$
is
$\tilde {\mu }$
is
![]() $\tilde {T}$
-invariant, integrating
$\tilde {T}$
-invariant, integrating
![]() $\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x= \tilde {\nu }_{T^{\gamma ^{\prime }}x}$
over
$\tilde {R}^{\gamma ^{\prime }}_{*}\tilde {\nu }_x= \tilde {\nu }_{T^{\gamma ^{\prime }}x}$
over
![]() $\tilde \mu $
gives
$\tilde \mu $
gives
![]() $\tilde {R} ^{\gamma ^{\prime }}_{*}\tilde {\theta }=\tilde {\theta }$
.
$\tilde {R} ^{\gamma ^{\prime }}_{*}\tilde {\theta }=\tilde {\theta }$
.
Recall that the map
![]() $\tilde {\alpha }$
is a
$\tilde {\alpha }$
is a
![]() ${\mathbf {CH}}_H$
-factor map. Moreover, for any
${\mathbf {CH}}_H$
-factor map. Moreover, for any
![]() $x\in \tilde {X}$
, we have
$x\in \tilde {X}$
, we have
![]() $\tilde {\alpha }^{*}\tilde {\nu } _x=\nu _x$
by observing that for any
$\tilde {\alpha }^{*}\tilde {\nu } _x=\nu _x$
by observing that for any
![]() $A\in \mathcal {B}a(\tilde {Y})$
,
$A\in \mathcal {B}a(\tilde {Y})$
,
Therefore,
which shows that
![]() $\tilde {\alpha }$
is a
$\tilde {\alpha }$
is a
![]() ${\mathbf {CHPrb}}_H$
-factor map.
${\mathbf {CHPrb}}_H$
-factor map.
It remains to show that
![]() $\tilde \pi $
is a
$\tilde \pi $
is a
![]() ${\mathbf {CHPrb}_{\Gamma }}$
-factor map, but this is a direct consequence of equation (9):
${\mathbf {CHPrb}_{\Gamma }}$
-factor map, but this is a direct consequence of equation (9):
Acknowledgments
A.J. was supported by DFG research fellowship JA 2512/3-1. We thank John Griesmer for helpful comments. We are sincerely grateful to an anonymous referee for a very constructive and detailed report, which helped to state a beautiful strengthening of our uniformity result and improve the presentation.