Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T04:28:39.606Z Has data issue: false hasContentIssue false
  • English
  • Français

The 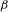$\unicode[STIX]{x1D6FD}$-transformation with a hole at 0

Part of: Low-dimensional dynamical systems Topological dynamics Measure-theoretic ergodic theory Discrete mathematics in relation to computer science Real functions Elementary number theory Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  25 March 2019

CHARLENE KALLE ,
DERONG KONG ,
NIELS LANGEVELD  and
WENXIA LI
CHARLENE KALLE
Affiliation:
Mathematical Institute, University of Leiden, PO Box 9512, 2300RA Leiden, The Netherlands email [email protected], [email protected]
DERONG KONG
Affiliation:
College of Mathematics and Statistics, Chongqing University, Chongqing401331, PR China email [email protected]
NIELS LANGEVELD
Affiliation:
Mathematical Institute, University of Leiden, PO Box 9512, 2300RA Leiden, The Netherlands email [email protected], [email protected]
WENXIA LI
Affiliation:
School of Mathematical Sciences, Shanghai Key Laboratory of PMMP, East China Normal University, Shanghai200062, PR China email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

For 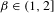$\unicode[STIX]{x1D6FD}\in (1,2]$ the 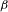$\unicode[STIX]{x1D6FD}$-transformation 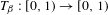$T_{\unicode[STIX]{x1D6FD}}:[0,1)\rightarrow [0,1)$ is defined by 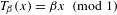$T_{\unicode[STIX]{x1D6FD}}(x)=\unicode[STIX]{x1D6FD}x\hspace{0.6em}({\rm mod}\hspace{0.2em}1)$. For 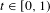$t\in [0,1)$ let 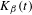$K_{\unicode[STIX]{x1D6FD}}(t)$ be the survivor set of $T_{\unicode[STIX]{x1D6FD}}$ with hole 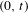$(0,t)$ given by

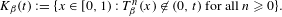$$\begin{eqnarray}K_{\unicode[STIX]{x1D6FD}}(t):=\{x\in [0,1):T_{\unicode[STIX]{x1D6FD}}^{n}(x)\not \in (0,t)\text{ for all }n\geq 0\}.\end{eqnarray}$$
In this paper we characterize the bifurcation set $E_{\unicode[STIX]{x1D6FD}}$ of all parameters 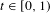$t\in [0,1)$ for which the set-valued function 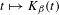$t\mapsto K_{\unicode[STIX]{x1D6FD}}(t)$ is not locally constant. We show that 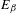$E_{\unicode[STIX]{x1D6FD}}$ is a Lebesgue null set of full Hausdorff dimension for all 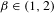$\unicode[STIX]{x1D6FD}\in (1,2)$. We prove that for Lebesgue almost every $\unicode[STIX]{x1D6FD}\in (1,2)$ the bifurcation set 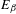$E_{\unicode[STIX]{x1D6FD}}$ contains infinitely many isolated points and infinitely many accumulation points arbitrarily close to zero. On the other hand, we show that the set of 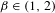$\unicode[STIX]{x1D6FD}\in (1,2)$ for which 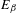$E_{\unicode[STIX]{x1D6FD}}$ contains no isolated points has zero Hausdorff dimension. These results contrast with the situation for 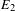$E_{2}$, the bifurcation set of the doubling map. Finally, we give for each 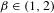$\unicode[STIX]{x1D6FD}\in (1,2)$ a lower and an upper bound for the value 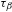$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}$ such that the Hausdorff dimension of 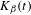$K_{\unicode[STIX]{x1D6FD}}(t)$ is positive if and only if 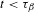$t<\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}$. We show that 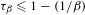$\unicode[STIX]{x1D70F}_{\unicode[STIX]{x1D6FD}}\leq 1-(1/\unicode[STIX]{x1D6FD})$ for all 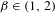$\unicode[STIX]{x1D6FD}\in (1,2)$.

Keywords

dimension theorylow-dimensional dynamicssymbolic dynamics

MSC classification

Primary: 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension 26A30: Singular functions, Cantor functions, functions with other special properties 37B10: Symbolic dynamics 37E05: Maps of the interval (piecewise continuous, continuous, smooth) 37E15: Combinatorial dynamics (types of periodic orbits)
Secondary: 11A63: Radix representation; digital problems 68R15: Combinatorics on words 28D05: Measure-preserving transformations
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 9 , September 2020 , pp. 2482 - 2514
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Alcaraz Barrera, R.. Topological and ergodic properties of symmetric sub-shifts. Discrete Contin. Dyn. Syst. 34(11) (2014), 4459–4486.Google Scholar
Bugeaud, Y. and Wang, B.. Distribution of full cylinders and the Diophantine properties of the orbits in 𝛽-expansions. J. Fractal Geom. 1(2) (2014), 221–241.Google Scholar
Bunimovich, L. and Yurchenko, A.. Where to place a hole to achieve a maximal escape rate. Israel J. Math. 182 (2011), 229–252.Google Scholar
Cao, C.-Y.. A result on the approximation properties of the orbit of 1 under the 𝛽-transformation. J. Math. Anal. Appl. 420(1) (2014), 242–256.Google Scholar
Carminati, C., Isola, S. and Tiozzo, G.. Continued fractions with SL(2, ℤ)-branches: combinatorics and entropy. Trans. Amer. Math. Soc. 370(7) (2018), 4927–4973.Google Scholar
Clark, L.. The 𝛽-transformation with a hole. Discrete Contin. Dyn. Syst. 36(3) (2016), 1249–1269.Google Scholar
Carminati, C. and Tiozzo, G.. The local Hölder exponent for the dimension of invariant subsets of the circle. Ergod. Th. & Dynam. Sys. 37(6) (2017), 1825–1840.Google Scholar
Dettmann, C.. Open circle maps: small hole asymptotics. Nonlinearity 26(1) (2013), 307–317.Google Scholar
de Vries, M., Komornik, V. and Loreti, P.. Topology of the set of univoque bases. Topology Appl. 205 (2016), 117–137.Google Scholar
Ge, Y. and Lü, F.. A note on inhomogeneous Diophantine approximation in beta-dynamical system. Bull. Aust. Math. Soc. 91(1) (2015), 34–40.Google Scholar
Glendinning, P. and Sidorov, N.. The doubling map with asymmetrical holes. Ergod. Th. & Dynam. Sys. 35(4) (2015), 1208–1228.Google Scholar
Komornik, V. and Loreti, P.. On the topological structure of univoque sets. J. Number Theory 122(1) (2007), 157–183.Google Scholar
Lothaire, M.. Algebraic Combinatorics on Words. Cambridge University Press, Cambridge, 2002.Google Scholar
Li, B., Persson, T., Wang, B. and Wu, J.. Diophantine approximation of the orbit of 1 in the dynamical system of beta expansions. Math. Z. 276(3–4) (2014), 799–827.Google Scholar
Lü, F. and Wu, J.. Diophantine analysis in beta-dynamical systems and Hausdorff dimensions. Adv. Math. 290 (2016), 919–937.Google Scholar
Nilsson, J.. On numbers badly approximable by $q$-adic rationals. PhD Thesis, Lund University and Université du Sud Toulon-Var, 2007.Google Scholar
Nilsson, J.. On numbers badly approximable by dyadic rationals. Israel J. Math. 171 (2009), 93–110.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Persson, T. and Schmeling, J.. Dyadic Diophantine approximation and Katok’s horseshoe approximation. Acta Arith. 132(3) (2008), 205–230.Google Scholar
Raith, P.. Hausdorff dimension for piecewise monotonic maps. Studia Math. 94(1) (1989), 17–33.Google Scholar
Raith, P.. Continuity of the Hausdorff dimension for piecewise monotonic maps. Israel J. Math. 80(1–2) (1992), 97–133.Google Scholar
Raith, P.. Continuity of the Hausdorff dimension for invariant subsets of interval maps. Acta Math. Univ. Comenian. (N.S.) 63(1) (1994), 39–53.Google Scholar
Rényi, A.. On algorithms for the generation of real numbers. Magyar Tud. Akad. Mat. Fiz. Oszt. Közl. 7 (1957), 265–293.Google Scholar
Schmeling, J.. Symbolic dynamics for 𝛽-shifts and self-normal numbers. Ergod. Th. & Dynam. Sys. 17(3) (1997), 675–694.Google Scholar
Sidorov, N.. Supercritical holes for the doubling map. Acta Math. Hungar. 143(2) (2014), 298–312.Google Scholar
Siromoney, R., Mathew, L., Dare, V. R. and Subramanian, K. G.. Infinite Lyndon words. Inform. Process. Lett. 50(2) (1994), 101–104.Google Scholar
Urbański, M.. On Hausdorff dimension of invariant sets for expanding maps of a circle. Ergod. Th. & Dynam. Sys. 6(2) (1986), 295–309.Google Scholar
Urbański, M.. Invariant subsets of expanding mappings of the circle. Ergod. Th. & Dynam. Sys. 7(4) (1987), 627–645.Google Scholar