Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T14:04:36.110Z Has data issue: false hasContentIssue false
  • English
  • Français

Transitivity of conservative diffeomorphisms isotopic to Anosov on 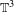$\mathbb{T}^{3}$

Published online by Cambridge University Press:  04 July 2016

MARTIN ANDERSSON  and
SHAOBO GAN
MARTIN ANDERSSON
Affiliation:
Departamento de Matemática Aplicada, Universidade Federal Fluminense, 24020-140, Niterói -RJ, Brazil
SHAOBO GAN
Affiliation:
LMAM, School of Mathematical Sciences, Peking University, Beijing 100871, China email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove transitivity for volume-preserving 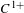$C^{1+}$ diffeomorphisms on 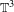$\mathbb{T}^{3}$ which are isotopic to a linear Anosov automorphism along a path of weakly partially hyperbolic diffeomorphisms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 1 , February 2018 , pp. 1 - 9
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Andersson, M.. Robust ergodic properties in partially hyperbolic dynamics. Trans. Amer. Math. Soc. 362(4) (2010), 1831–1867.Google Scholar
Andersson, M.. Transitivity of conservative toral endomorphisms. Nonlinearity 29(3) (2016), 1047–1055.Google Scholar
Barreira, L. and Pesin, Y. B.. Introduction to Smooth Ergodic Theory (Graduate Studies in Mathematics, 148) . American Mathematical Society, Providence, RI, 2013.Google Scholar
Bonatti, C. and Crovisier, S.. Récurrence et généricité. Invent. Math. 158(1) (2004), 33–104.Google Scholar
Bonatti, C. and Viana, M.. SRB measures for partially hyperbolic systems whose central direction is mostly contracting. Israel J. Math. 115 (2000), 157–193.Google Scholar
Brin, M. I. and Pesin, Ja. B.. Partially hyperbolic dynamical systems. Izv. Akad. Nauk SSSR Ser. Mat. 38 (1974), 170–212.Google Scholar
Fisher, T., Potrie, R. and Sambarino, M.. Dynamical coherence of partially hyperbolic diffeomorphisms of tori isotopic to Anosov. Math. Z. 278(1–2) (2014), 149–168.Google Scholar
Franks, J.. Anosov diffeomorphisms. Global Analysis (Berkeley, CA, 1968) (Proceedings of Symposia Pure Mathematics, 14) . American Mathematical Society, Providence, RI, 1970, pp. 61–93.Google Scholar
Givant, S. and Halmos, P.. Introduction to Boolean Algebras (Undergraduate Texts in Mathematics) . Springer, New York, 2009.Google Scholar
Hammerlindl, A. and Ures, R.. Ergodicity and partial hyperbolicity on the 3-torus. Commun. Contemp. Math. 16(04) (2014),1350038.Google Scholar
Hirsch, M. W., Pugh, C. C. and Shub, M.. Invariant Manifolds (Lecture Notes in Mathematics, 583) . Springer, Berlin, 1977.Google Scholar
Potrie, R.. Partial hyperbolicity and foliations in T3 . J. Mod. Dyn. 9(1) (2015), 81–121.Google Scholar
Rodriguez Hertz, J.. Genericity of nonuniform hyperbolicity in dimension 3. J. Mod. Dyn. 6(1) (2012), 121–138.Google Scholar
Tahzibi, A.. Stably ergodic diffeomorphisms which are not partially hyperbolic. Israel J. Math. 142 (2004), 315–344.Google Scholar
Walters, P.. Anosov diffeomorphisms are topologically stable. Topology 9(1) (1970), 71–78.Google Scholar