Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-30T20:04:44.206Z Has data issue: false hasContentIssue false
  • English
  • Français

Topologically irreducible representations of the Banach $\ast$-algebra associated with a dynamical system

Published online by Cambridge University Press:  24 January 2017

AKI KISHIMOTO  and
JUN TOMIYAMA
AKI KISHIMOTO
Affiliation:
Hokkaido University, Japan email [email protected]
JUN TOMIYAMA
Affiliation:
Tokyo Metropolitan University, Japan email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We describe (infinite-dimensional) irreducible representations of the crossed product C$^{\ast }$-algebra associated with a topological dynamical system (based on $\mathbb{Z}$) and we show that their restrictions to the underlying 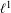$\ell ^{1}$-Banach $\ast$-algebra are not algebraically irreducible under mild conditions on the dynamical system. The above description of irreducible representations has two ingredients, ergodic measures on the space and ergodic extensions for the tensor product with type I factors, the latter of which may not have been explicitly taken up before but which will be explored by means of examples. A new class of ergodic measures is also constructed for irrational rotations on the circle.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 5 , August 2018 , pp. 1768 - 1790
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Dixmier, J.. Von Neumann Algebras, translation of Les Algebres d’Operateurs dans l’Espace Hilbertien. North-Holland, Amsterdam, 1981.Google Scholar
de Jeu, M., Svensson, C. and Tomiyama, J.. On the Banach ∗-algebra crossed product associated with a topological dynamical system. J. Funct. Anal. 262 (2012), 4746–4765.CrossRefGoogle Scholar
de Jeu, M. and Tomiyama, J.. Maximal abelian subalgebras and projections in two Banach algebras associated with a topological dynamical system. Studia Math. 208 (2012), 47–75.CrossRefGoogle Scholar
de Jeu, M. and Tomiyama, J.. Noncommutative spectral sysnthesis for the involutive Banach algebra associated with a topological dynamical system. Banach J. Math. Anal. 7 (2013), 103–135.CrossRefGoogle Scholar
de Jeu, M. and Tomiyama, J.. Algebraically irreducible representations and structure space of the Banach algebra associated with a topological dynamical system. Adv. in Math. 301 (2016), 79–115.CrossRefGoogle Scholar
Kadison, R. V.. Irreducible operator algebras. Proc. Natl. Acad. Sci. USA 43 (1957), 273–276.CrossRefGoogle ScholarPubMed
Pedersen, G. K.. C∗ -algebras and their Automorphism Groups. Academic Press, London, 1979.Google Scholar
Sakai, S.. C∗ -algebras and W∗ -algebras. Springer, Berlin, 1971.Google Scholar
Tomiyama, J.. Invitation to C∗ -algebras and Topological Dynamics. World Scientific, Singapore, 1987.CrossRefGoogle Scholar
Tomiyama, J.. The Interplay Between Topological Dynamics and Theory of C∗ -algebras (Lecture Note, 2) . Research Institute of Mathematics, Seoul, 1992.Google Scholar
Tomiyama, J. and Cho, M.. Note on the structure of non-commutative $\ell ^{1}$ -algebras associated with topological dynamical system. Preprint, 2015.Google Scholar