Hostname: page-component-745bb68f8f-5r2nc Total loading time: 0 Render date: 2025-02-05T16:07:37.419Z Has data issue: false hasContentIssue false
  • English
  • Français

Time almost periodicity for solutions of Toda lattice equation with almost periodic initial datum

Part of: Ordinary differential operators Elliptic equations and systems General first-order equations and systems Difference and functional equations Difference equations

Published online by Cambridge University Press:  27 January 2025

HAOXI ZHAO  and
HONGYU CHENG
HAOXI ZHAO
Affiliation:
Chern Institute of Mathematics and LPMC, Nankai University, Tianjin 300071, P.R. China Tianjin Nankai High School, Tianjin 300199, P.R. China (e-mail: [email protected])
HONGYU CHENG*
Affiliation:
School of Mathematical Sciences, Tiangong University, Tianjin 300387, P.R. China
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper analyzes the initial value problem for the Toda lattice with almost periodic initial data: let 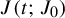$J(t; J_{0})$ denote the family of Jacobi matrices which are solutions of the Toda flow equation with initial condition 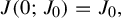$J(0; J_{0})=J_{0},$ then, the given almost periodic datum 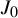$J_{0}$ is a discrete linear Schrödinger operator with almost periodic potential, which plays a fundamental role in our considerations. We show that, under some given hypotheses, the spectrum of the Schrödinger operator is pure absolute continuous and homogeneous (measure-theoretically) by establishing exponential asymptotics on the size of spectral gaps. These two conclusions enable us to show the boundedness and almost periodicity in the time of solutions for Toda lattice equation with almost periodic initial data. As a consequence, our result presents a positive answer to the discrete Deift’s conjecture [Some open problems in random matrix theory and the theory of integrable systems. Integrable Systems and Random Matrices (Contemporary Mathematics, 458). American Mathematical Society, Providence, RI, 2008, pp. 419–430; Some open problems in random matrix theory and the theory of integrable systems. II. SIGMA Symmetry Integrability Geom. Methods Appl. 13 (2017), Paper no. 016].

Keywords

time almost periodicityToda latticeinitial datumJocabic operator

MSC classification

Primary: 39A24: Almost periodic solutions 35J10: Schrödinger operator
Secondary: 35F25: Initial value problems for nonlinear first-order equations 34L40: Particular operators (Dirac, one-dimensional Schrödinger, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , First View , pp. 1 - 40
Check for updates
Copyright
© The Author(s), 2025. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Avila, A.. The absolutely continuous spectrum of the almost Mathieu operator. Preprint, 2008, arXiv:0810.2965.Google Scholar
Avila, A.. On the spectrum and Lyapunov exponent of limit periodic Schrödinger operators. Comm. Math. Phys. 288(3) (2009), 907–918.CrossRefGoogle Scholar
Avila, A.. Almost reducibility and absolute continuity I. Preprint, 2010, arXiv:1006.0704.Google Scholar
Avila, A.. Global theory of one-frequency Schrödinger operators. Acta Math. 215(1) (2015), 1–54.CrossRefGoogle Scholar
Avila, A.. KAM, Lyapunov exponents and the spectral dichotomy for one-frequency Schrödinger operators. Preprint, 2023, arXiv:2307.11071.Google Scholar
Avila, A. and Damanik, D.. Absolute continuity of the integrated density of states for the almost Mathieu operator with non-critical coupling. Invent. Math. 172(2) (2008), 439–453.CrossRefGoogle Scholar
Avila, A., Fayad, B. and Krikorian, R.. A KAM scheme for cocycles with Liouvillean frequencies. Geom. Funct. Anal. 21(5) (2011), 1001–1019.CrossRefGoogle Scholar
Avila, A. and Jitomirskaya, S.. Almost localization and almost reducibility. J. Eur. Math. Soc. (JEMS) 12(1) (2010), 93–131.CrossRefGoogle Scholar
Avila, A., Last, Y., Shamis, M. and Zhou, Q.. On the abominable properties of the almost Mathieu operator with well-approximated frequencies. Duke Math. J. 173(4) (2024), 603–672.CrossRefGoogle Scholar
Avron, J.-E. and Simon, B.. Transient and recurrent spectrum. J. Funct. Anal. 43(1) (1981), 1–31.CrossRefGoogle Scholar
Bellissard, J., Lima, R. and Testard, D.. Almost periodic Schrödinger operators. Mathematics + Physics. Volume 1. World Scientific Publishing, Singapore, 1985, pp. 1–64.Google Scholar
Biasco, L., Massetti, J. E. and Procesi, M.. An abstract Birkhoff normal form theorem and exponential type stability of the 1D NLS. Comm. Math. Phys. 375(3) (2020), 2089–2153.CrossRefGoogle Scholar
Binder, I., Damanik, D., Goldstein, M. and Lukic, M.. Almost periodicity in time of solutions of the KdV equation. Duke Math. J. 167(14) (2018), 2633–2678.CrossRefGoogle Scholar
Binder, I., Damanik, D., Lukic, M. and Vandenboom, T.. Almost periodicity in time of solutions of the Toda lattice. C. R. Math. Acad. Sci. Soc. R. Can. 40(1) (2018), 1–28.Google Scholar
Bochner, S.. Beiträge zur Theorie der fastperiodischen Funktionen. Math. Ann. 96(1) (1927), 119–147.CrossRefGoogle Scholar
Bourgain, J.. Construction of approximative and almost periodic solutions of perturbed linear Schrödinger and wave equations. Geom. Funct. Anal. 6(2) (1996), 201–230.CrossRefGoogle Scholar
Bourgain, J.. Green’s Function Estimates for Lattice Schrödinger Operators and Applications (Annals of Mathematics Studies, 158). Princeton University Press, Princeton, NJ, 2005.CrossRefGoogle Scholar
Bourgain, J.. On invariant tori of full dimension for 1D periodic NLS. J. Funct. Anal. 229(1) (2005), 62–94.CrossRefGoogle Scholar
Bourgain, J. and Goldstein, M.. On nonperturbative localization with quasi-periodic potential. Ann. of Math. (2) 152(3) (2000), 835–879.CrossRefGoogle Scholar
Cai, A., Chavaudret, C., You, J. and Zhou, Q.. Sharp Hölder continuity of the Lyapunov exponent of finitely differentiable quasi-periodic cocycles. Math. Z. 291(3–4) (2019), 931–958.CrossRefGoogle Scholar
Carleson, L.. On ${H}^{\infty }$ in multiply connected domains. Conference on Harmonic Analysis in Honor of Antoni Zygmund, Vol. I, II (Chicago, IL, 1981) (The Wadsworth & Brooks/Cole Mathematics Series). Wadsworth, Belmont, CA, 1983, pp. 349–372.Google Scholar
Craig, W.. The trace formula for Schrödinger operators on the line. Comm. Math. Phys. 126(2) (1989), 379–407.CrossRefGoogle Scholar
Damanik, D. and Fillman, J.. Spectral properties of limit-periodic operators. Analysis and Geometry on Graphs and Manifolds (London Mathematical Society Lecture Note Series, 461). Cambridge University Press, Cambridge, 2020, pp. 382–444.CrossRefGoogle Scholar
Damanik, D. and Fillman, J.. Gap labelling for discrete one-dimensional ergodic Schrödinger operators. From Complex Analysis to Operator Theory—A Panorama (Operator Theory: Advances and Applications, 291). Birkhäuser/Springer, Cham, 2023, pp. 341–404.CrossRefGoogle Scholar
Damanik, D. and Gan, Z.. Spectral properties of limit-periodic Schrödinger operators. Commun. Pure Appl. Anal. 10(3) (2011), 859–871.CrossRefGoogle Scholar
Damanik, D. and Goldstein, M.. On the inverse spectral problem for the quasi-periodic Schrödinger equation. Publ. Math. Inst. Hautes Études Sci. 119 (2014), 217–401.CrossRefGoogle Scholar
Damanik, D. and Goldstein, M.. On the existence and uniqueness of global solutions for the KdV equation with quasi-periodic initial data. J. Amer. Math. Soc. 29(3) (2016), 825–856.CrossRefGoogle Scholar
Damanik, D., Goldstein, M. and Lukic, M.. The spectrum of a Schrödinger operator with small quasi-periodic potential is homogeneous. J. Spectr. Theory 6(2) (2016), 415–427.CrossRefGoogle Scholar
Damanik, D., Goldstein, M., Schlag, W. and Voda, M.. Homogeneity of the spectrum for quasi-periodic Schrödinger operators. J. Eur. Math. Soc. (JEMS) 20(12) (2018), 3073–3111.CrossRefGoogle Scholar
Damanik, D. and Gorodetski, A.. An extension of the Kunz–Souillard approach to localization in one dimension and applications to almost-periodic Schrödinger operators. Adv. Math. 297 (2016), 149–173.CrossRefGoogle Scholar
Damanik, D., Li, Y. and Xu, F.. The quasi-periodic Cauchy problem for the generalized Benjamin–Bona–Mahony equation on the real line. J. Funct. Anal. 286 (2024), 110238.CrossRefGoogle Scholar
Damanik, D., Li, Y. and Xu, F.. Local existence and uniqueness of spatially quasi-periodic solutions to the generalized KdV equation. J. Math. Pures Appl. (9) 186 (2024), 251–302.CrossRefGoogle Scholar
Deift, P.. Some open problems in random matrix theory and the theory of integrable systems. Integrable Systems and Random Matrices (Contemporary Mathematics, 458). American Mathematical Society, Providence, RI, 2008, pp. 419–430.CrossRefGoogle Scholar
Deift, P.. Some open problems in random matrix theory and the theory of integrable systems. II. SIGMA Symmetry Integrability Geom. Methods Appl. 13 (2017), Paper no. 016.Google Scholar
Dinaburg, E. I. and Sinaĭ, J. G.. The one-dimensional Schrödinger equation with quasiperiodic potential. Funktsional. Anal. i Prilozhen. 9(4) (1975), 8–21.Google Scholar
Eliasson, L. H.. Floquet solutions for the $1$ -dimensional quasi-periodic Schrödinger equation. Comm. Math. Phys. 146(3) (1992), 447–482.CrossRefGoogle Scholar
Fillman, J.. Spectral homogeneity of discrete one-dimensional limit-periodic operators. J. Spectr. Theory 7(1) (2017), 201–226.CrossRefGoogle Scholar
Fillman, J. and Lukic, M.. Spectral homogeneity of limit-periodic Schrödinger operators. J. Spectr. Theory, 7(2) (2017), 387–406.CrossRefGoogle Scholar
Geng, J.. Invariant tori of full dimension for a nonlinear Schrödinger equation. J. Differential Equations 252(1) (2012), 1–34.CrossRefGoogle Scholar
Geng, J. and Xu, X.. Almost periodic solutions of one dimensional Schrödinger equation with the external parameters. J. Dynam. Differential Equations 25(2) (2013), 435–450.CrossRefGoogle Scholar
Gesztesy, F. and Yuditskii, P.. Spectral properties of a class of reflectionless Schrödinger operators. J. Funct. Anal. 241(2) (2006), 486–527.CrossRefGoogle Scholar
Goldstein, M. and Schlag, W.. Hölder continuity of the integrated density of states for quasi-periodic Schrödinger equations and averages of shifts of subharmonic functions. Ann. of Math. (2) 154(1) (2001), 155–203.CrossRefGoogle Scholar
Hadj-Amor, S.. Hölder continuity of the rotation number for quasi-periodic co-cycles in SL(2, ℝ). Comm. Math. Phys. 287(2) (2009), 565–588.CrossRefGoogle Scholar
Herman, M.-R.. Une méthode pour minorer les exposants de Lyapounov et quelques exemples montrant le caractère local d’un théorème d’Arnol’d et de Moser sur le tore de dimension $2$ . Comment. Math. Helv. 58(3) (1983), 453–502.CrossRefGoogle Scholar
Hou, X. and You, J.. Almost reducibility and non-perturbative reducibility of quasi-periodic linear systems. Invent. Math. 190(1) (2012), 209–260.CrossRefGoogle Scholar
Johnson, R. and Moser, J.. The rotation number for almost periodic potentials. Comm. Math. Phys. 84(3) (1982), 403–438.CrossRefGoogle Scholar
Krikorian, R.. Reducibility, differentiable rigidity and Lyapunov exponents for quasi-periodic cocycles on $T\times SL(2,\mathbb{R})$ . Preprint, 2004, arXiv:math/0402333.Google Scholar
Leguil, M., You, J., Zhao, Z. and Zhou, Q.. Asymptotics of spectral gaps of quasi-periodic Schrödinger operators. Camb. J. Math. 12(4) (2024), 753–830.CrossRefGoogle Scholar
Liang, X., Wang, H., Zhou, Q. and Zhou, T.. Traveling fronts for Fisher-KPP lattice equations in almost-periodic media. Ann. Inst. H. Poincaré C Anal. Non Linéaire 41(5) (2024), 1179–1237.CrossRefGoogle Scholar
Liu, W. and Yuan, X.. Spectral gaps of almost Mathieu operators in the exponential regime. J. Fractal Geom. 2(1) (2015), 1–51.CrossRefGoogle Scholar
Montalto, R. and Procesi, M.. Linear Schrödinger equation with an almost periodic potential. SIAM J. Math. Anal. 53(1) (2021), 386–434.CrossRefGoogle Scholar
Moser, J.. An example of a Schrödinger equation with almost periodic potential and nowhere dense spectrum. Comment. Math. Helv. 56(2) (1981), 198–224.CrossRefGoogle Scholar
Moser, J. and Pöschel, J.. An extension of a result by Dinaburg and Sinaĭ on quasiperiodic potentials. Comment. Math. Helv. 59(1) (1984), 39–85.CrossRefGoogle Scholar
Nadin, G. and Rossi, L.. Generalized transition fronts for one-dimensional almost periodic Fisher-KPP equations. Arch. Ration. Mech. Anal. 223(3) (2017), 1239–1267.CrossRefGoogle Scholar
Pastur, L. A. and Tkachenko, V. A.. On the spectral theory of the one-dimensional Schrödinger operator with limit-periodic potential. Dokl. Akad. Nauk SSSR 279(5) (1984), 1050–1053.Google Scholar
Pastur, L. A. and Tkachenko, V. A.. Spectral theory of a class of one-dimensional Schrödinger operators with limit-periodic potentials. Tr. Moskov. Mat. Obshch. 51 (1988), 114–168, 258 pp.Google Scholar
Poltoratski, A. and Remling, C.. Reflectionless Herglotz functions and Jacobi matrices. Comm. Math. Phys. 288(3) (2009), 1007–1021.CrossRefGoogle Scholar
Puig, J.. Cantor spectrum for the almost Mathieu operator. Comm. Math. Phys. 244(2) (2004), 297–309.CrossRefGoogle Scholar
Puig, J.. A nonperturbative Eliasson’s reducibility theorem. Nonlinearity 19(2) (2006), 355–376.CrossRefGoogle Scholar
Shi, Y. and Yuan, X.. Exponential decay of the lengths of the spectral gaps for the extended Harper’s model with a Liouvillean frequency. J. Dynam. Differential Equations 31(4) (2019), 1921–1953.CrossRefGoogle Scholar
Simon, B.. Almost periodic Schrödinger operators: a review. Adv. Appl. Math. 3(4) (1982), 463–490.CrossRefGoogle Scholar
Simon, B.. Szegő’s Theorem and Its Descendants: Spectral Theory for L2 Perturbations of Orthogonal Polynomials (M. B. Porter Lectures). Princeton University Press, Princeton, NJ, 2011.Google Scholar
Sodin, M. and Yuditskii, P.. Almost periodic Jacobi matrices with homogeneous spectrum, infinite-dimensional Jacobi inversion, and Hardy spaces of character-automorphic functions. J. Geom. Anal. 7(3) (1997), 387–435.CrossRefGoogle Scholar
Sodin, M. and Yuditskii, S.. Almost periodic Sturm–Liouville operators with Cantor homogeneous spectrum. Comment. Math. Helv. 70(4) (1995), 639–658.CrossRefGoogle Scholar
Sorets, E. and Spencer, T.. Positive Lyapunov exponents for Schrödinger operators with quasi-periodic potentials. Comm. Math. Phys. 142(3) (1991), 543–566.CrossRefGoogle Scholar
Teschl, G.. Jacobi Operators and Completely Integrable Nonlinear Lattices (Mathematical Surveys and Monographs, 72). American Mathematical Society, Providence, RI, 2000.Google Scholar
Toda, M.. Vibration of a chain with nonlinear interaction. J. Phys. Soc. Japan 22(2) (1967), 431–436.CrossRefGoogle Scholar
Tsugawa, K.. Local well-posedness of the KdV equation with quasi-periodic initial data. SIAM J. Math. Anal. 44(5) (2012), 3412–3428.CrossRefGoogle Scholar
Vinnikov, V. and Yuditskii, P.. Functional models for almost periodic Jacobi matrices and the Toda hierarchy. Mat. Fiz. Anal. Geom. 9(2) (2002), 206–219.Google Scholar
Wu, J. and Geng, J.. Almost periodic solutions for a class of semilinear quantum harmonic oscillators. Discrete Contin. Dyn. Syst. 31(3) (2011), 997–1015.CrossRefGoogle Scholar
Yoccoz, J.-C.. Some questions and remarks about cocycles. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 447–458.Google Scholar