Article contents
Thurston equivalence for rational maps with clusters
Published online by Cambridge University Press: 08 May 2012
Abstract
We investigate rational maps with period-one and period-two cluster cycles. Given the definition of a cluster, we show that, in the case where the degree is 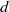 $d$ and the cluster is fixed, the Thurston class of a rational map is fixed by the combinatorial rotation number
$d$ and the cluster is fixed, the Thurston class of a rational map is fixed by the combinatorial rotation number 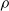 $\rho $ and the critical displacement
$\rho $ and the critical displacement 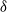 $\delta $of the cluster cycle. The same result will also be proved in the case where the rational map is quadratic and has a period-two cluster cycle, and we will also show that the statement is no longer true in the higher-degree case.
$\delta $of the cluster cycle. The same result will also be proved in the case where the rational map is quadratic and has a period-two cluster cycle, and we will also show that the statement is no longer true in the higher-degree case.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 2
- Cited by


