Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:27:52.350Z Has data issue: false hasContentIssue false
  • English
  • Français

There are no deviations for the ergodic averages of Giulietti–Liverani horocycle flows on the two-torus

Part of: Smooth dynamical systems: general theory Dynamical systems with hyperbolic behavior Ergodic theory

Published online by Cambridge University Press:  18 March 2021

VIVIANE BALADI Open the ORCID record for VIVIANE BALADI [Opens in a new window]
VIVIANE BALADI*
Affiliation:
Laboratoire de Probabilités, Statistique et Modélisation, CNRS, Sorbonne Université, Université de Paris, 4, Place Jussieu, 75005Paris, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that the ergodic integrals for the horocycle flow on the two-torus associated by Giulietti and Liverani with an Anosov diffeomorphism either grow linearly or are bounded; in other words, there are no deviations. For this, we use the topological invariance of the Artin–Mazur zeta function to exclude resonances outside the open unit disc. Transfer operators acting on suitable spaces of anisotropic distributions and their Ruelle determinants are the key tools used in the proof. As a bonus, we show that for any 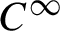$C^\infty $ Anosov diffeomorphism F on the two-torus, the correlations for the measure of maximal entropy and 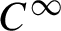$C^\infty $ observables decay with a rate strictly smaller than 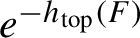$e^{-h_{\mathrm {top}}(F)}$ . We compare our results with very recent related work of Forni.

Keywords

low dimensional dynamicssmooth dynamicstransfer operatorszeta functions

MSC classification

Primary: 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Secondary: 37C30: Zeta functions, (Ruelle-Frobenius) transfer operators, and other functional analytic techniques in dynamical systems 37C40: Smooth ergodic theory, invariant measures 37A20: Orbit equivalence, cocycles, ergodic equivalence relations 37A25: Ergodicity, mixing, rates of mixing
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 2: Anatole Katok Memorial Issue Part 1: Special Issue of Ergodic Theory and Dynamical Systems , February 2022 , pp. 500 - 513
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Adam, A.. Horocycle averages on closed manifolds and transfer operators. Preprint, 2018, arXiv:1809.04062.Google Scholar
Baladi, V.. Dynamical Zeta Functions and Dynamical Determinants for Hyperbolic Maps (Ergebnisse der Mathematik und ihrer Grenzgebiete, 68). Springer, Cham, 2018.10.1007/978-3-319-77661-3CrossRefGoogle Scholar
Baladi, V. and Tsujii, M.. Dynamical determinants and spectrum for hyperbolic diffeomorphisms. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469). American Mathematical Society, Providence, RI, 2008, pp. 29–68.10.1090/conm/469/09160CrossRefGoogle Scholar
Carrand, J.. Logarithmic bounds for ergodic averages of constant type rotation number flows on the torus: a short proof. Preprint, 2020, arXiv:2012.07481.Google Scholar
Flaminio, L. and Forni, G.. Invariant distributions and time averages for horocycle flows. Duke Math. J. 119 (2003), 465–526.10.1215/S0012-7094-03-11932-8CrossRefGoogle Scholar
Forni, G.. On the equidistribution of unstable curves for pseudo-Anosov diffeomorphisms of compact surfaces. Preprint, 2020, arXiv:2007.03144.10.1017/etds.2021.119CrossRefGoogle Scholar
Giulietti, P. and Liverani, C.. Parabolic dynamics and anisotropic Banach spaces. JEMS 21 (2019), 2793–2858.10.4171/JEMS/892CrossRefGoogle Scholar
Gouëzel, S. and Liverani, C.. Compact locally maximal hyperbolic sets for smooth maps: fine statistical properties. J. Differential Geom. 79 (2008), 433–477.10.4310/jdg/1213798184CrossRefGoogle Scholar
Hasselblatt, B.. Regularity of the Anosov splitting and of horospheric foliations. Ergod. Th. & Dynam. Sys. 14 (1994), 645–666.10.1017/S0143385700008105CrossRefGoogle Scholar
Herman, M.-R.. Sur la conjugaison différentiable des difféomorphismes du cercle à des rotations. Publ. Math. Inst. Hautes Études Sci. 49 (1979), 5–233.10.1007/BF02684798CrossRefGoogle Scholar
Hiraide, K.. A simple proof of the Franks–Newhouse theorem on codimension-one Anosov diffeomorphisms. Ergod. Th. & Dynam. Sys. 21 (2001), 801–806.10.1017/S0143385701001390CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems (Encyclopedia Mathematics and Applications, 54). Cambridge University Press, Cambridge, 1995.10.1017/CBO9780511809187CrossRefGoogle Scholar
McCutcheon, R.. The Gottschalk–Hedlund theorem. Amer. Math. Monthly 106 (1999), 670–672.10.1080/00029890.1999.12005101CrossRefGoogle Scholar
Young, L.-S.. What are SRB measures, and which dynamical systems have them?. J. Stat. Phys. 108 (2002), 733–754.10.1023/A:1019762724717CrossRefGoogle Scholar