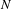Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-27T03:55:35.413Z Has data issue: false hasContentIssue false
  • English
  • Français

Syzygy sequences of the $N$-center problem

Published online by Cambridge University Press:  22 September 2016

KUO-CHANG CHEN  and
GUOWEI YU
KUO-CHANG CHEN
Affiliation:
Department of Mathematics, National Tsing Hua University, Hsinchu 30013, Taiwan email [email protected]
GUOWEI YU
Affiliation:
Department of Mathematics, University of Toronto, Toronto, Ontario M5S 2E4, Canada email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of this paper is to consider the 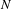$N$-center problem with collinear centers, to identify its syzygy sequences that can be realized by minimizers of the Lagrangian action functional and to count the number of such syzygy sequences. In particular, we show that the number of such realizable syzygy sequences of length 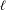$\ell$ greater than or equal to two for the 3-center problem is at least 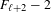$F_{\ell +2}-2$, where 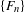$\{F_{n}\}$ is the Fibonacci sequence. Moreover, with fixed length 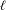$\ell$, the density of such realizable syzygy sequences of length 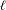$\ell$ for the 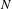$N$-center problem approaches one as 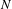$N$ increases to infinity. Using reflection symmetry, the minimizers that we found can be extended to periodic solutions.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 566 - 582
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bolotin, S. V.. Nonintegrability of the n-center problem for n > 2. Vestnik Moskov. Gos. Univ. Ser. I Mat. Mekh. 3 (1984), 65–68.Google Scholar
Castelli, R.. On the variational approach to the one and $N$ -centre problem with weak forces. PhD Thesis, University of Milano, Bicocca, 2009.Google Scholar
Chen, K.-C.. Removing collision singularities from action minimizers for the N-body problem with free boundaries. Arch. Ration. Mech. Anal. 181 (2006), 311–331.Google Scholar
Chen, K.-C.. Existence and minimizing properties of retrograde orbits to the three-body problem with various choices of masses. Ann. of Math. 167 (2008), 325–348.Google Scholar
Chenciner, A.. Action minimizing solutions of the Newtonian n-body problem: from homology to symmetry. Proc. Int. Congress of Mathematicians (Beijing, China, 2002). Vol. III. Higher Ed. Press, Beijing, China, 2002, pp. 279–294.Google Scholar
Chenciner, A.. Symmetries and simple solutions of the classical n-body problem. Proc. 14th Int. Congress on Mathematical Physics (Lisbon, Portugal, 2003). World Scientific, Hackensack, NJ, 2005, pp. 4–20.Google Scholar
Chenciner, A. and Montgomery, R.. A remarkable periodic solution of the three-body problem in the case of equal masses. Ann. of Math. 152 (2000), 881–901.CrossRefGoogle Scholar
Diacu, F.. A generic property of the bounded syzygy solutions. Proc. Amer. Math. Soc. 116 (1992), 809–812.Google Scholar
Dullin, H. R. and Montgomery, R.. Syzygies in the two center problem. Nonlinearity 29 (2016), 1212–1237.Google Scholar
Ferrario, D. and Terracini, S.. On the existence of collisionless equivariant minimizers for the classical n-body problem. Invent. Math. 155 (2004), 305–362.Google Scholar
Fusco, G., Gronchi, G. F. and Negrini, P.. Platonic polyhedra, topological constraints and periodic solutions of the classical N-body problem. Invent. Math. 185 (2011), 283–332.Google Scholar
Gordon, W.. A minimizing property of Keplerian orbits. Amer. J. Math. 99 (1977), 961–971.Google Scholar
Klein, M. and Knauf, A.. Classical Planar Scattering by Coulombic Potentials (Lecture Notes in Physics, M13) . Springer, Berlin, 1992.CrossRefGoogle Scholar
Knauf, A. and Taimanov, I. A.. On the Integrability of the n-centre problem. Math. Ann. 331 (2004), 631–649.Google Scholar
Moeckel, R. and Montgomery, R.. Realizing all reduced syzygy sequences in the planar three-body problem. Nonlinearity 28 (2015), 1919–1935.Google Scholar
Moeckel, R., Montgomery, R. and Venturelli, A.. From brake to syzygy. Arch. Ration. Mech. Anal. 204 (2012), 1009–1060.CrossRefGoogle Scholar
Montgomery, R.. Infinitely many syzygies. Arch. Ration. Mech. Anal. 164 (2002), 311–340.Google Scholar
Soave, N. and Terracini, S.. Symbolic dynamics for the N-centre problem at negative energies. Discrete Contin. Dyn. Syst. A 32 (2012), 3245–3301.CrossRefGoogle Scholar
Terracini, S. and Venturelli, A.. Symmetric trajectories for the 2N-body problem with equal masses. Arch. Ration. Mech. Anal. 184 (2007), 465–493.Google Scholar
Venturelli, A.. Application de la minimisation de l’action au problème des $N$ - corps dans le plan et dans l’espace. PhD Thesis, Université Denis Diderot in Paris, 2002.Google Scholar
Whittaker, E. T.. A Treatise on the Analytical Dynamics of Particles and Rigid Bodies: With an Introduction to the Problem of Three Bodies, 4th edn. Cambridge University Press, Cambridge, 1937.Google Scholar
Yu, G.. Periodic solutions of the planar N-center problem with topological constraints. Discrete Contin. Dyn. Syst. A to appear.Google Scholar