No CrossRef data available.
Article contents
Symbolic dynamics for pointwise hyperbolic systems on open regions
Published online by Cambridge University Press: 10 September 2024
Abstract
Under certain conditions, we construct a countable Markov partition for pointwise hyperbolic diffeomorphism 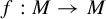 $f:M\rightarrow M$ on an open invariant subset
$f:M\rightarrow M$ on an open invariant subset 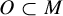 $O\subset M$, which allows the Lyapunov exponents to be zero. From this partition, we define a symbolic extension that is finite-to-one and onto a subset of O that carries the same finite f-invariant measures as O. Our method relies upon shadowing theory of a recurrent-pointwise-pseudo-orbit that we introduce. As a canonical application, we estimate the number of closed orbits for f.
$O\subset M$, which allows the Lyapunov exponents to be zero. From this partition, we define a symbolic extension that is finite-to-one and onto a subset of O that carries the same finite f-invariant measures as O. Our method relies upon shadowing theory of a recurrent-pointwise-pseudo-orbit that we introduce. As a canonical application, we estimate the number of closed orbits for f.
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press



