No CrossRef data available.
Published online by Cambridge University Press: 23 May 2024
Bedford and Smillie [A symbolic characterization of the horseshoe locus in the Hénon family. Ergod. Th. & Dynam. Sys. 37(5) (2017), 1389–1412] classified the dynamics of the Hénon map 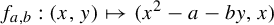 $f_{a, b} : (x, y)\mapsto (x^2-a-by, x)$ defined on
$f_{a, b} : (x, y)\mapsto (x^2-a-by, x)$ defined on 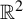 $\mathbb {R}^2$ in terms of a symbolic dynamics when
$\mathbb {R}^2$ in terms of a symbolic dynamics when 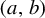 $(a, b)$ is close to the boundary of the horseshoe locus. The purpose of the current article is to generalize their results for all
$(a, b)$ is close to the boundary of the horseshoe locus. The purpose of the current article is to generalize their results for all 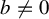 $b\ne 0$ (including the case
$b\ne 0$ (including the case 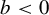 $b < 0$ as well). The method of the proof is first to regard
$b < 0$ as well). The method of the proof is first to regard 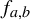 $f_{a, b}$ as a complex dynamical system in
$f_{a, b}$ as a complex dynamical system in 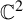 $\mathbb {C}^2$ and second to introduce the new Markov-like partition in
$\mathbb {C}^2$ and second to introduce the new Markov-like partition in 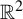 $\mathbb {R}^2$ constructed by us [On parameter loci of the Hénon family. Comm. Math. Phys. 361(2) (2018), 343–414].
$\mathbb {R}^2$ constructed by us [On parameter loci of the Hénon family. Comm. Math. Phys. 361(2) (2018), 343–414].