Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-28T11:47:34.007Z Has data issue: false hasContentIssue false
  • English
  • Français

Symbol ratio minimax sequences in the lexicographic order

Published online by Cambridge University Press:  05 August 2014

PHILIP BOYLAND ,
ANDRÉ DE CARVALHO  and
TOBY HALL
PHILIP BOYLAND
Affiliation:
Department of Mathematics, University of Florida, 372 Little Hall, Gainesville, FL 32611-8105, USA
ANDRÉ DE CARVALHO
Affiliation:
Departamento de Matemática Aplicada, IME-USP, Rua Do Matão 1010, Cidade Universitária, 05508-090 São Paulo SP, Brazil
TOBY HALL
Affiliation:
Department of Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Consider the space of sequences of 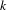$k$ letters ordered lexicographically. We study the set 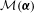${\mathcal{M}}(\boldsymbol{{\it\alpha}})$ of all maximal sequences for which the asymptotic proportions $\boldsymbol{{\it\alpha}}$ of the letters are prescribed, where a sequence is said to be maximal if it is at least as great as all of its tails. The infimum of 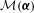${\mathcal{M}}(\boldsymbol{{\it\alpha}})$ is called the $\boldsymbol{{\it\alpha}}$-infimax sequence, or the $\boldsymbol{{\it\alpha}}$-minimax sequence if the infimum is a minimum. We give an algorithm which yields all infimax sequences, and show that the infimax is not a minimax if and only if it is the $\boldsymbol{{\it\alpha}}$-infimax for every $\boldsymbol{{\it\alpha}}$ in a simplex of dimension 1 or greater. These results have applications to the theory of rotation sets of beta-shifts and torus homeomorphisms.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 35 , Issue 8 , December 2015 , pp. 2371 - 2396
Copyright
© Cambridge University Press, 2014 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Arnoux, P.. Sturmian sequences. Substitutions in Dynamics, Arithmetics and Combinatorics (Lecture Notes in Mathematics, 1794). Eds. Berthé, V., Ferenczi, S., Mauduit, C. and Siegel, A.. Springer, Berlin, 2002, pp. 143–198.Google Scholar
Arnoux, P. and Rauzy, G.. Représentation géométrique de suites de complexité 2n + 1. Bull. Soc. Math. France 119(2) (1991), 199–215.CrossRefGoogle Scholar
Berstel, J. and Perrin, D.. The origins of combinatorics on words. European J. Combin. 28(3) (2007), 996–1022.CrossRefGoogle Scholar
Berthé, V., Ferenczi, S. and Zamboni, L.. Interactions between dynamics, arithmetics and combinatorics: the good, the bad, and the ugly. Algebraic and Topological Dynamics (Contemporary Mathematics, 385). American Mathematical Society, Providence, RI, 2005, pp. 333–364.CrossRefGoogle Scholar
Birkhoff, G.. Extensions of Jentzsch’s theorem. Trans. Amer. Math. Soc. 85 (1957), 219–227.Google Scholar
Borovikov, V.. On the intersection of a sequence of simplexes. Uspehi Matem. Nauk (N.S.) 7(6(52)) (1952), 179–180.Google Scholar
Bruin, H.. Renormalization in a class of interval translation maps of d branches. Dyn. Syst. 22(1) (2007), 11–24.CrossRefGoogle Scholar
Bruin, H. and Troubetzkoy, S.. The Gauss map on a class of interval translation mappings. Israel J. Math. 137 (2003), 125–148.CrossRefGoogle Scholar
Carroll, J. E.. Birkhoff’s contraction coefficient. Linear Algebra Appl. 389 (2004), 227–234.CrossRefGoogle Scholar
Cassaigne, J. and Nicolas, F.. Factor complexity. Combinatorics, Automata and Number Theory (Encyclopedia of Mathematical Applications, 135). Cambridge University Press, Cambridge, 2010, pp. 163–247.CrossRefGoogle Scholar
de Melo, W. and van Strien, S.. One-dimensional Dynamics (Ergebnisse der Mathematik und ihrer Grenzgebiete (3) [Results in Mathematics and Related Areas (3)], 25). Springer, Berlin, 1993.Google Scholar
Ferenczi, S., Holton, C. and Zamboni, L.. Structure of three-interval exchange transformations. II. A combinatorial description of the trajectories. J. Anal. Math. 89 (2003), 239–276.CrossRefGoogle Scholar
Ferenczi, S. and Zamboni, L.. Clustering words and interval exchanges. J. Integer Seq. 16(2) (2013), Article 13.2.1, 9.Google Scholar
Gambaudo, J.-M., Lanford, O. III and Tresser, C.. Dynamique symbolique des rotations. C. R. Acad. Sci. Paris Sér. I Math. 299(16) (1984), 823–826.Google Scholar
Gottschalk, W.. Substitution minimal sets. Trans. Amer. Math. Soc. 109 (1963), 467–491.CrossRefGoogle Scholar
Hedlund, G. A.. Sturmian minimal sets. Amer. J. Math. 66 (1944), 605–620.CrossRefGoogle Scholar
Jenkinson, O.. A partial order on × 2-invariant measures. Math. Res. Lett. 15(5) (2008), 893–900.CrossRefGoogle Scholar
Jenkinson, O.. Balanced words and majorization. Discrete Math. Algorithms Appl. 1(4) (2009), 463–483.CrossRefGoogle Scholar
Lopez, L.-M. and Narbel, P.. Substitutions and interval exchange transformations of rotation class. Theoret. Comput. Sci. 255(1–2) (2001), 323–344.CrossRefGoogle Scholar
Lyndon, R. C.. On Burnside’s problem. Trans. Amer. Math. Soc. 77 (1954), 202–215.Google Scholar
Morse, M. and Hedlund, G. A.. Symbolic dynamics II. Sturmian trajectories. Amer. J. Math. 62 (1940), 1–42.CrossRefGoogle Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.CrossRefGoogle Scholar
Rauzy, G.. Échanges d’intervalles et transformations induites. Acta Arith. 34(4) (1979), 315–328.CrossRefGoogle Scholar
Schweiger, F.. Multidimensional Continued Fractions. Oxford Science Publications, Oxford University Press, Oxford, 2000.CrossRefGoogle Scholar
Veerman, P.. Symbolic dynamics of order-preserving orbits. Phys. D 29(1–2) (1987), 191–201.CrossRefGoogle Scholar
Ziemian, K.. Rotation sets for subshifts of finite type. Fund. Math. 146(2) (1995), 189–201.CrossRefGoogle Scholar