Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:14:10.875Z Has data issue: false hasContentIssue false
  • English
  • Français

Subsystems, Perron numbers, and continuous homomorphisms of Bernoulli shifts

Published online by Cambridge University Press:  19 September 2008

Selim Tuncel
Selim Tuncel
Affiliation:
Department of Mathematics, University of Washington, Seattle, WA 98195, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

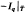Let S, T be subshifts of finite type, with Markov measures p, q on them, and let φ: (S, p) → (T, q) be a block code. Let Ip, Iq denote the information cocycles of p, q. For a subshift of finite type ⊂T, the pressure of equals that of 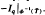. Applying this to Bernoulli shifts and using finiteness conditions on Perron numbers, we have the following. If the probability vector p = (p1…, pk+1) is such that the distinct transcendental elements of {p1/pk+1…pk/pk+1) are algebraically independent then the Bernoulli shift B(p) has finitely many Bernoulli images by block codes.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 9 , Issue 3 , September 1989 , pp. 561 - 570
Copyright
Copyright © Cambridge University Press 1989

References

REFERENCES

[1]Bourbaki, N.. Commutative Algebra, Elements of Mathematics. Addison-Wesley: Reading, Mass., 1972.Google Scholar
[2]Boyle, M. & Tuncel, S.. Infinite-to-one codes and Markov measures. Trans. Amer. Math. Soc. 285 (1984), 657–684.CrossRefGoogle Scholar
[3]Handelman, D.. Positive matrices and dimension groups affiliated to C*-algebras and topological Markov chains. J. Operator Theory 6 (1981), 55–74.Google Scholar
[4]del Junco, A., Keane, M., Kitchens, B., Marcus, B. & Swanson, L.. Continuous homomorphisms of Bernoulli schemes. Progress in Math. 10, pp. 91–111. Birkhäuser: Boston, 1981.Google Scholar
[5]Keller, G.. To appear in Proc. Amer. Math. Soc.Google Scholar
[6]Kitchens, B. & Tuncel, S.. On measures induced on subsystems. Dynamical Systems, SLN 1342, pp. 455–464. Springer: New York, 1989.Google Scholar
[7]Lind, D.. The entropies of topological Markov shifts and a related class of algebraic integers. Ergod.Th. & Dynam. Sys. 4 (1984), 283–300.CrossRefGoogle Scholar
[8]Seneta, E.. Non-negative Matrices and Markov Chains. Springer: New York, 1981.Google Scholar
[9]Smorodinsky, M.. Block codes for Bernoulli shifts. Israel J. Math. 49 (1984), 325–330.Google Scholar
[10]Tuncel, S.. Conditional pressure and coding. Israel J. Math. 39 (1981), 101–112.Google Scholar
[11]Walters, P.. An Introduction to Ergodic Theory. Springer: New York, 1982.Google Scholar
[12]Weiss, E.. Algebraic Number Theory. McGraw-Hill: New York, 1963.Google Scholar