Article contents
Strong stochastic stability for non-uniformly expanding maps
Published online by Cambridge University Press: 06 August 2012
Abstract
We consider random perturbations of discrete-time dynamical systems. We give sufficient conditions for the stochastic stability of certain classes of maps, in a strong sense. This improves the main result in Alves and Araújo [Random perturbations of non-uniformly expanding maps. Astérisque 286 (2003), 25–62], where the stochastic stability in the 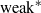 $\mathrm {weak}^*$ topology was proved. Here, under slightly weaker assumptions on the random perturbations, we obtain a stronger version of stochastic stability: convergence of the density of the stationary measure to the density of the Sinai–Ruelle–Bowen (SRB) measure of the unperturbed system in the
$\mathrm {weak}^*$ topology was proved. Here, under slightly weaker assumptions on the random perturbations, we obtain a stronger version of stochastic stability: convergence of the density of the stationary measure to the density of the Sinai–Ruelle–Bowen (SRB) measure of the unperturbed system in the 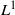 $L^1$-norm. As an application of our results, we obtain strong stochastic stability for two classes of non-uniformly expanding maps. The first one is an open class of local diffeomorphisms introduced in Alves, Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398] and the second one is the class of Viana maps.
$L^1$-norm. As an application of our results, we obtain strong stochastic stability for two classes of non-uniformly expanding maps. The first one is an open class of local diffeomorphisms introduced in Alves, Bonatti and Viana [SRB measures for partially hyperbolic systems whose central direction is mostly expanding. Invent. Math. 140 (2000), 351–398] and the second one is the class of Viana maps.
- Type
- Research Article
- Information
- Copyright
- Copyright © 2012 Cambridge University Press
References
- 13
- Cited by


