Hostname: page-component-586b7cd67f-g8jcs Total loading time: 0 Render date: 2024-11-27T21:00:16.008Z Has data issue: false hasContentIssue false
  • English
  • Français

Spectral theory of $\mathbb{Z}^{d}$ substitutions

Published online by Cambridge University Press:  20 October 2016

ALAN BARTLETT
ALAN BARTLETT*
Affiliation:
University of Washington Tacoma, Interdisciplinary Arts and Sciences, Box 358436, 1900 Commerce Street, Tacoma, WA 98402, USA email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

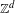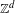In this paper, we generalize and develop results of Queffélec allowing us to characterize the spectrum of an aperiodic $\mathbb{Z}^{d}$ substitution. Specifically, we describe the Fourier coefficients of mutually singular measures of pure type giving rise to the maximal spectral type of the translation operator on 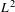$L^{2}$, without any assumptions on primitivity or height, and show singularity for aperiodic bijective commutative 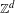$\mathbb{Z}^{d}$ substitutions. Moreover, we provide a simple algorithm to determine the spectrum of aperiodic 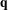$\mathbf{q}$-substitutions, and use this to show singularity of Queffélec’s non-commutative bijective substitution, as well as the Table tiling, answering an open question of Solomyak. Finally, we show that every ergodic matrix of measures on a compact metric space can be diagonalized, which we use in the proof of the main result.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 4 , June 2018 , pp. 1289 - 1341
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baake, M., Gähler, F. and Grimm, U.. Examples of substitution systems and their factors. J. Integer Seq. 16 (2013), art. 13.2.14 (18 pp).Google Scholar
Baake, M. and Grimm, U.. Aperiodic Order. Vol. 1. A Mathematical Invitation (Encyclopedia of Mathematics and its Applications, 149) . Cambridge University Press, Cambridge, 2013.Google Scholar
Baake, M. and Grimm, U.. Squirals and beyond: substitution tilings with singular continuous spectrum. Ergod. Th. & Dynam. Sys. 34 (2014), 1077–1102.Google Scholar
Baake, M., Lenz, D. and Van Enter, A.. Dynamical versus diffraction spectrum for structures with finite local complexity, Preprint, 2013, arXiv:1307.7518.Google Scholar
Bartlett, A.. Spectral theory of $\mathbb{Z}^{d}$ substitutions. Ph.D. thesis, University of Washington, Seattle, 2015.Google Scholar
Bezuglyi, S., Kwiatkowski, J., Medynets, K. and Solomyak, B.. Invariant measures on stationary Bratteli diagrams. Ergod. Th. & Dynam. Sys. 30 (2010), 973–1007.Google Scholar
Cortez, M. and Solomyak, B.. Invariant measures for non-primitive tiling substitutions. J. Anal. Math. 115(1) (2011), 293–342.Google Scholar
Dekking, F.. The spectrum of a dynamical system arising from substitutions of constant length. Z. Wahrscheinlichkeitstheorie Verw. Gebiete 41 (1978), 221–239.Google Scholar
Dworkin, S.. Spectral theory and X-ray diffraction. J. Math. Phys. 34 (1993), 2965–2967.Google Scholar
Frank, N. P.. Substitution sequences in ℤ d with a nonsimple Lebesgue component in the spectrum. Ergod. Th. & Dynam. Sys. 23(2) (2003), 519–532.Google Scholar
Frank, N. P.. Multidimensional constant-length substitution sequences. Topol. Appl. 152(12) (2005), 44–69.CrossRefGoogle Scholar
Gantmacher, F. R.. Applications of the Theory of Matrices. Dover Publications, New York, 2005.Google Scholar
Horn, R. and Johnson, C.. Topics in Matrix Analysis. Cambridge University Press, Cambridge, 1991.Google Scholar
Lee, J.-Y., Moody, R. V. and Solomyak, B.. Pure point dynamical and diffraction spectra. Ann. Henri Poincaré 3 (2002), 1003–1018.Google Scholar
Michel, P.. Stricte ergodicité d’ensembles minimaux de substitutions. C. R. Acad. Sci. Paris 278 (1974), 811–813.Google Scholar
Mossé, B.. Reconnaissabilité des substitutions et complexité des suites automatiques. Bull. Soc. Math. France 124 (1996), 329–346.Google Scholar
Mozes, S.. Tilings, substitution systems and dynamical systems generated by them. J. Anal. Math. 53 (1989), 139–186.Google Scholar
Pansiot, J.. Decidability of periodicity for infinite words. RAIRO Inform. Théor. Appl. 20 (1986), 43–46.Google Scholar
Queffélec, M.. Substitution Dynamical Systems, Spectral Analysis, 2nd edn. Springer, Berlin, 2010.Google Scholar
Radin, C.. Miles of Tiles. Amerfican Mathematical Society, Providence, RI, 1999.Google Scholar
Robinson, E. A.. On the table and the chair. Indag. Math. 10(4) (1999), 581–599.Google Scholar
Solomyak, B.. Nonperiodicity implies unique composition for self-similar translationally finite tilings. Discrete Comput. Geom. 20(2) (1998), 265–279.CrossRefGoogle Scholar
Šreider, Y. A.. The structure of maximal ideals in rings of measures with convolution. Mat. Sbornik (N.S.) 27(69) (1950), 297–318; Amer. Math. Soc., translation no. 81, Providence, 1953.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, New York, 1982.Google Scholar