No CrossRef data available.
Article contents
A spectral strong approximation theorem for measure-preserving actions
Published online by Cambridge University Press: 06 September 2018
Abstract
Let  $\unicode[STIX]{x1D6E4}$ be a finitely generated group acting by probability measure-preserving maps on the standard Borel space
$\unicode[STIX]{x1D6E4}$ be a finitely generated group acting by probability measure-preserving maps on the standard Borel space 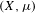 $(X,\unicode[STIX]{x1D707})$. We show that if
$(X,\unicode[STIX]{x1D707})$. We show that if 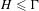 $H\leq \unicode[STIX]{x1D6E4}$ is a subgroup with relative spectral radius greater than the global spectral radius of the action, then
$H\leq \unicode[STIX]{x1D6E4}$ is a subgroup with relative spectral radius greater than the global spectral radius of the action, then 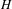 $H$ acts with finitely many ergodic components and spectral gap on
$H$ acts with finitely many ergodic components and spectral gap on 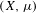 $(X,\unicode[STIX]{x1D707})$. This answers a question of Shalom who proved this for normal subgroups.
$(X,\unicode[STIX]{x1D707})$. This answers a question of Shalom who proved this for normal subgroups.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018


