Hostname: page-component-586b7cd67f-t7czq Total loading time: 0 Render date: 2024-12-03T19:23:10.195Z Has data issue: false hasContentIssue false
  • English
  • Français

Spatial determinism for a free Z2-action

Published online by Cambridge University Press:  16 December 2011

ROBERT BURTON  and
KYEWON K. PARK
ROBERT BURTON
Affiliation:
Department of Mathematics, Oregon State University, Corvallis, OR, USA (email: [email protected])
KYEWON K. PARK
Affiliation:
Department of Mathematics, Ajou University, Suwon 443-749, Korea (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We extend the idea of bilateral determinism of a free Z-action by D. Ornstein and B. Weiss to a free Z2-action. We show that we have a ‘stronger’ spatial determinism for Z2-actions: to determine the complete Z2-name of a point, it is enough to know the name of a fraction of the orbit whose density can be made arbitrarily small. Moreover, for zero-entropy Z2-actions, we prove that there exists a partition 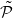such that the 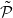-names of an arbitrarily small one-sided cone determine the points.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 32 , Issue 2: Daniel J. Rudolph – in Memoriam , April 2012 , pp. 479 - 489
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Burton, R.. An asymptotic definition of K-groups of automorphisms and a non-Bernoullian counter-example. Z. Wahr. verw. Geb. 47 (1979), 205–212.CrossRefGoogle Scholar
[2]Burton, R. and Steif, J.. Coupling surfaces and weak Bernoulli in one and higher dimensions. Adv. Math. 132(1) (1997), 1–23.Google Scholar
[3]Conze, J. P.. Entropie d’un groupe abelien de transformations. Z. Wahr. verw. Geb. 25 (1972), 11–30.Google Scholar
[4]Dou, D., Hwang, W. and Park, K. K.. Entropy dimension of topological dynamical systems. Trans. Amer. Math. Soc. 363 (2011), 659–680.CrossRefGoogle Scholar
[5]Dou, D., Hwang, W. and Park, K. K.. Entropy dimension of measure preserving systems. Preprint.Google Scholar
[6]Ferenczi, S. and Park, K.. Entropy dimensions and a class of constructive examples. J. Contin. Discrete Dyn. Syst. 17 (2007), 133–141.Google Scholar
[7]Krieger, W.. On the entropy and generators of measure preserving transformations. Trans. Amer. Math. Soc. 149 (1970), 453–464.CrossRefGoogle Scholar
[8]Ornstein, D. and Weiss, B.. Every transformation is bilaterally deterministic. Israel J. Math. 21 (1975), 154–158.Google Scholar
[9]Ornstein, D. and Weiss, B.. Entropy and isomorphism theorem for actions of amenable groups. J. Anal. Math. 48 (1987), 1–141.Google Scholar
[10]Ornstein, D. and Weiss, B.. The Shannon–McMillan–Breiman theorem for a class of amenable groups. Israel J. Math. 44 (1983), 53–60.CrossRefGoogle Scholar
[11]Thouvenot, J.-P.. Personal communication.Google Scholar