Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-26T17:22:40.483Z Has data issue: false hasContentIssue false
  • English
  • Français

Smale endomorphisms over graph-directed Markov systems

Part of: Dynamical systems with hyperbolic behavior Probability theory on algebraic and topological structures Smooth dynamical systems: general theory Ergodic theory Measures, integration, derivative, holomorphy Probabilistic theory: distribution modulo $1$; metric theory of algorithms

Published online by Cambridge University Press:  08 June 2020

EUGEN MIHAILESCU  and
MARIUSZ URBAŃSKI
EUGEN MIHAILESCU
Affiliation:
Institute of Mathematics of the Romanian Academy, P.O. Box 1-764, RO 014700, Bucharest, Romania (e-mail: [email protected])
MARIUSZ URBAŃSKI
Affiliation:
Department of Mathematics, University of North Texas, Denton, TX76203-1430, USA (e-mail: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We study Smale skew product endomorphisms (introduced in Mihailescu and Urbański [Skew product Smale endomorphisms over countable shifts of finite type. Ergod. Th. & Dynam. Sys. doi: 10.1017/etds.2019.31. Published online June 2019]) now over countable graph-directed Markov systems, and we prove the exact dimensionality of conditional measures in fibers, and then the global exact dimensionality of the equilibrium measure itself. Our results apply to large classes of systems and have many applications. They apply, for instance, to natural extensions of graph-directed Markov systems. Another application is to skew products over parabolic systems. We also give applications in ergodic number theory, for example to the continued fraction expansion, and the backward fraction expansion. In the end we obtain a general formula for the Hausdorff (and pointwise) dimension of equilibrium measures with respect to the induced maps of natural extensions 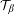${\mathcal{T}}_{\unicode[STIX]{x1D6FD}}$ of 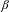$\unicode[STIX]{x1D6FD}$-maps 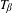$T_{\unicode[STIX]{x1D6FD}}$, for arbitrary 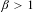$\unicode[STIX]{x1D6FD}>1$.

Keywords

Hausdorff dimension of measuresthermodynamic formalism of Smale endomorphismsbeta-mapsinverse limitscontinued fractions

MSC classification

Primary: 37D35: Thermodynamic formalism, variational principles, equilibrium states 37A35: Entropy and other invariants, isomorphism, classification 37C45: Dimension theory of dynamical systems 37A45: Relations with number theory and harmonic analysis 11K55: Metric theory of other algorithms and expansions; measure and Hausdorff dimension
Secondary: 46G10: Vector-valued measures and integration 60B05: Probability measures on topological spaces
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 8 , August 2021 , pp. 2508 - 2541
Check for updates
Copyright
© The Author(s) 2020. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aaronson, J., Bromberg, M. and Nakada, H.. Discrepancy skew products and affine random walks. Israel J. Math. 221 (2017), 973–1010.Google Scholar
Adler, R. and Flatto, L.. The backward continued fraction map and geodesic flow. Ergod. Th. & Dynam. Sys. 4 (1984), 487–492.Google Scholar
Allaart, P. and Kong, D.. On the continuity of the Hausdorff dimension of the univoque set. Adv. Math. 354 (2019), 106729.Google Scholar
Barreira, L., Pesin, Y. and Schmeling, J.. Dimension and product structure of hyperbolic measures. Ann. of Math. 149 (1999), 755–783.Google Scholar
Bosma, W., Jager, H. and Wiedijk, F.. Some metrical observations on the approximation by continued fractions. Nederl. Akad. Wetensch. Indag. Math. 45 (1983), 281–299.Google Scholar
Bruin, H. and Todd, M.. Equilibrium states for interval maps: the potential - tlog|Df|. Ann. Sci. Éc. Norm. Supér. 42 (2009), 559–600.Google Scholar
Dajani, K. and Kalle, C.. Local dimensions for random 𝛽-transformations. New York J. Math. 19 (2013), 285–303.Google Scholar
Dajani, K. and Kraaikamp, C.. Ergodic Theory of Numbers. MAA, Washington, DC, 2002.Google Scholar
Dajani, K., Kraaikamp, C. and Solomyak, B.. The natural extension of the 𝛽-transformation. Acta Math. Hungar 73 (1996), 97–109.Google Scholar
Feng, D. J. and Hu, H.. Dimension theory of iterated function systems. Comm. Pure Appl. Math. 62 (2009), 1435–1500.Google Scholar
Fornaess, J. E. and Mihailescu, E.. Equilibrium measures on saddle sets of holomorphic maps on ℙ2 . Math. Ann. 356 (2013), 1471–1491.Google Scholar
Glendinning, P. and Sidorov, N.. Unique representations of real numbers in non-integer bases. Math. Res. Lett. 8 (2001), 535–543.Google Scholar
Hanus, P., Mauldin, D. and Urbański, M.. Thermodynamic formalism and multifractal analysis of conformal infinite iterated function systems. Acta Math. Hungar. 96 (2002), 27–98.Google Scholar
Iosifescu, M. and Kraaikamp, C.. Metrical Theory of Continued Fractions (Mathematics and its Applications). Kluwer Academic Publishers, Dordrecht, 2002.Google Scholar
Kessebohmer, M., Munday, S. and Stratmann, B.. Strong renewal theorems and Lyapunov spectra for 𝛼-Farey and 𝛼-Lüroth systems. Ergod. Th. & Dynam. Sys. 32(3) (2012), 989–1017.Google Scholar
Mané, R.. Ergodic Theory and Differentiable Dynamics. Springer, Berlin, 1987.Google Scholar
Mauldin, D. and Urbański, M.. Dimensions and measures in infinite iterated function systems. Proc. Lond. Math. Soc. (3) 73 (1996), 105–154.Google Scholar
Mauldin, D. and Urbański, M.. Parabolic iterated function systems. Ergod. Th. & Dynam. Sys. 20 (2000), 1423–1447.Google Scholar
Mauldin, D. and Urbański, M.. Gibbs states on the symbolic space over an infinite alphabet. Israel J. Math. 125 (2001), 93–130.Google Scholar
Mauldin, D. and Urbański, M.. Fractal measures for parabolic IFS. Adv. Math. 168 (2002), 225–253.Google Scholar
Mauldin, D. and Urbański, M.. Graph Directed Markov Systems: Geometry and Dynamics of Limit Sets. Cambridge University Press, Cambridge, 2003.Google Scholar
Mihailescu, E.. On a class of stable conditional measures. Ergod. Th. & Dynam. Sys. 31 (2011), 1499–1515.Google Scholar
Mihailescu, E.. Asymptotic distributions of preimages for endomorphisms. Ergod. Th. & Dynam. Sys. 31 (2011), 911–935.Google Scholar
Mihailescu, E.. Unstable directions and fractal dimension for skew products with overlaps in fibers. Math. Z. 269 (2011), 733–750.Google Scholar
Mihailescu, E.. Local geometry and dynamical behavior on folded basic sets. J. Stat. Phys. 142 (2011), 154–167.Google Scholar
Mihailescu, E.. Equilibrium measures, prehistories distributions and fractal dimensions for endomorphisms. Disc. Cont. Dyn. Syst. 32 (2012), 2485–2502.Google Scholar
Mihailescu, E.. On some coding and mixing properties on folded fractals. Monatsh. Math. 167 (2012), 241–255.Google Scholar
Mihailescu, E.. Approximations for Gibbs states of arbitrary Hölder potentials on hyperbolic folded sets. Discrete Contin. Dyn. Syst. 32(3) (2012), 961–975.Google Scholar
Mihailescu, E. and Stratmann, B.. Upper estimates for stable dimensions on fractal sets with variable numbers of foldings. Int. Math. Res. Not. 2014(23) (2014), 6474–6496.Google Scholar
Mihailescu, E. and Urbański, M.. Skew product Smale endomorphisms over countable shifts of finite type. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2019.31. Published online 25 June 2019.Google Scholar
Mihailescu, E. and Urbański, M.. Random countable iterated function systems with overlaps and applications. Adv. Math. 298 (2016), 726–758.Google Scholar
Mihailescu, E. and Urbanski, M.. Overlap functions for measures in conformal iterated function systems. J. Stat. Phys. 162 (2016), 43–62.Google Scholar
Mihailescu, E. and Urbanski, M.. Measure-theoretic degrees and topological pressure for non-expanding transformations. J. Funct. Anal. 267(8) (2014), 2823–2845.Google Scholar
Mihailescu, E. and Urbański, M.. Hausdorff Dimension of Limit Sets of Countable Conformal Iterated Function Systems with Overlaps (Contemporary Mathematics, 600). American Mathematical Society, Providence, RI, 2013, pp. 273–290.Google Scholar
Parry, W.. On the 𝛽-expansions of real numbers. Acta Math. Acad. Sci. Hungar. 11 (1960), 401–416.Google Scholar
Pesin, Y.. Dimension Theory in Dynamical Systems (Chicago Lectures in Mathematics). University of Chicago Press, Chicago, 1997.Google Scholar
Pollicott, M. and Weiss, H.. Multifractal analysis of Lyapunov exponent for continued fraction and Manneville-Pomeau transformations and applications to diophantine approximation. Commun. Math. Phys. 207 (1999), 145–171.Google Scholar
Rokhlin, V. A.. Lectures on the theory of entropy of transformations with invariant measures. Russian Math. Surveys 22 (1967), 1–54.Google Scholar
Ruelle, D.. Thermodynamic Formalism (The Mathematical Structures of Equilibrium Statistical Mechanics). 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Ruelle, D.. Elements of Differentiable Dynamics and Bifurcation Theory. Academic Press, Boston, MA, 1989.Google Scholar
Sarig, O.. Thermodynamic formalism for countable Markov shifts. Ergod. Th. & Dynam. Sys. 19 (1999), 1565–1593.Google Scholar
Sarig, O.. Existence of Gibbs measures for countable Markov shifts. Proc. Amer. Math. Soc. 131 (2003), 1751–1758.Google Scholar
Schweiger, P.. Ergodic Theory of Fibered Systems and Metric Number Theory. Oxford University Press, New York, 1995.Google Scholar
Urbański, M.. Parabolic Cantor sets. Fund. Math. 151 (1996), 241–277.Google Scholar
Young, L. S.. Dimension, entropy and Lyapunov exponents. Ergod. Th. & Dynam. Sys. 2 (1982), 109–124.Google Scholar