Hostname: page-component-cd9895bd7-mkpzs Total loading time: 0 Render date: 2024-12-27T04:42:22.207Z Has data issue: false hasContentIssue false
  • English
  • Français

Sets of large values of correlation functions for polynomial cubic configurations

Published online by Cambridge University Press:  19 September 2016

V. BERGELSON  and
A. LEIBMAN
V. BERGELSON
Affiliation:
Department of Mathematics, The Ohio State University, OH 43210, USA email [email protected], [email protected]
A. LEIBMAN
Affiliation:
Department of Mathematics, The Ohio State University, OH 43210, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We prove that for any set 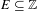$E\subseteq \mathbb{Z}$ with upper Banach density 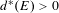$d^{\ast }(E)>0$, the set ‘of cubic configurations’ in 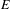$E$ is large in the following sense: for any 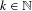$k\in \mathbb{N}$ and any 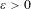$\unicode[STIX]{x1D700}>0$, the set

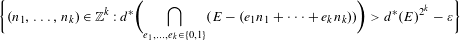$$\begin{eqnarray}\displaystyle \biggl\{(n_{1},\ldots ,n_{k})\in \mathbb{Z}^{k}:d^{\ast }\biggl(\mathop{\bigcap }_{e_{1},\ldots ,e_{k}\in \{0,1\}}(E-(e_{1}n_{1}+\cdots +e_{k}n_{k}))\biggr)>d^{\ast }(E)^{2^{k}}-\unicode[STIX]{x1D700}\biggr\} & & \displaystyle \nonumber\end{eqnarray}$$
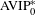is an $\text{AVIP}_{0}^{\ast }$-set. We then generalize this result to the case of ‘polynomial cubic configurations’ 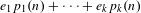$e_{1}p_{1}(n)+\cdots +e_{k}p_{k}(n)$, where the polynomials 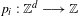$p_{i}:\mathbb{Z}^{d}\longrightarrow \mathbb{Z}$ are assumed to be sufficiently algebraically independent.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 2 , April 2018 , pp. 499 - 522
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auslander, L., Green, L. and Hahn, F.. Flows on Homogeneous Spaces (Annals of Mathematics Studies, 53) . Princeton University Press, Princeton, NJ, 1963.CrossRefGoogle Scholar
Bergelson, V.. Ergodic Ramsey theory—An Update, Ergodic Theory of ℤ d -Actions (London Mathematical Society Lecture Note Series, 228) . Cambridge University Press, Cambridge, 1996, pp. 1–61.Google Scholar
Bergelson, V.. The multifarious Poincaré recurrence theorem. Descriptive Set Theory and Dynamical Systems (London Mathematical Society Lecture Note Series, 277) . Cambridge University Press, Cambridge, 2000, pp. 31–57.CrossRefGoogle Scholar
Bergelson, V.. Minimal idempotents and ergodic Ramsey theory. Topics in Dynamics and Ergodic Theory (London Mathematical Society Lecture Note Series, 310) . Cambridge University Press, Cambridge, 2003, pp. 8–39.Google Scholar
Bergelson, V.. Ergodic Ramsey Theory (Contemporary Mathematics, 65) . American Mathematical Society, Providence, RI, 1987, pp. 63–87.Google Scholar
Bergelson, V. and Downarowicz, T.. Large sets of integers and hierarchy of mixing properties of measure preserving systems. Colloq. Math. 110(1) (2008), 117–150.CrossRefGoogle Scholar
Bergelson, V., Furstenberg, H. and McCutcheon, R.. IP-sets and polynomial recurrence. Ergod. Th. & Dynam. Sys. 16 (1996), 963–974.Google Scholar
Bergelson, V., Furstenberg, H. and Weiss, B.. Piecewise-Bohr sets of integers and combinatorial number theory. Topics in Discrete Mathematics (Algorithms and Combinatorics, 26) . Springer, Berlin, 2006, pp. 13–37.CrossRefGoogle Scholar
Bergelson, V., Host, B. and Kra, B.. Multiple recurrence and nilsequences., With an appendix by I. Ruzsa. Invent. Math. 160(2) (2005), 261–303.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. Set-polynomials and polynomial extension of the Hales–Jewett theorem. Ann. of Math. (2) 150 (1999), 33–75.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. Cubic averages and large intersections. Contemp. Math. 631 (2015), 5–20.CrossRefGoogle Scholar
Bergelson, V. and Leibman, A.. IP $_{r}^{\ast }$ -recurrence and nilsystems. Preprint, 2016, arXiv:1604.02489.Google Scholar
Bergelson, V., Leibman, A. and Lesigne, E.. Weyl complexity of a system of polynomials, and constructions in combinatorial number theory. J. Anal. Math. 103 (2007), 47–92.CrossRefGoogle Scholar
Bergelson, V., Leibman, A. and Lesigne, E.. Intersective polynomials and the polynomial Szemerédi theorem. Adv. Math. 219 (2008), 369–388.Google Scholar
Bergelson, V. and McCutcheon, R.. Central sets and a non-commutative Roth theorem. Amer. J. Math. 129(5) (2007), 1251–1275.Google Scholar
Bergelson, V. and McCutcheon, R.. Idempotent ultrafilters, multiple weak mixing and Szemerédi’s theorem for generalized polynomials. J. Anal. Math. 111 (2010), 77–130.Google Scholar
Frantzikinakis, N.. Multiple correlation sequences and nilsequences. Invent. Math. 202 (2015), 875–892.Google Scholar
Frantzikinakis, N. and Kra, B.. Polynomial averages converge to the product of integrals. Israel J. Math. 148 (2005), 267–276.Google Scholar
Furstenberg, H.. Recurrence in Ergodic Theory and Combinatorial Number Theory. Princeton University Press, Princeton, NJ, 1981.CrossRefGoogle Scholar
Furstenberg, H. and Weiss, B.. Topological dynamics and combinatorial number theory. J. D’Anal. Math. 34 (1978), 61–85.Google Scholar
Gillis, J.. Note on a property of measurable sets. J. Lond. Math. Soc. (2) 11(2) (1936), 139–141.Google Scholar
Hindman, N.. Finite sums from sequences within cells of a partition of ℕ. J. Combin. Theory Ser. A 17 (1974), 1–11.Google Scholar
Host, B. and Kra, B.. Averaging along cubes. Modern Dynamical Systems and Applications. Cambridge University Press, Cambridge, 2004, pp. 123–144.Google Scholar
Host, B. and Kra, B.. Non-conventional ergodic averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 397–488.CrossRefGoogle Scholar
Host, B. and Kra, B.. Nil–Bohr sets of integers. Ergod. Th. & Dynam. Sys. 31 (2011), 113–142.Google Scholar
Host, B., Kra, B. and Maass, A.. Complexity of nilsystems and systems lacking nilfactors. J. Anal. Math. 124 (2014), 261–295.Google Scholar
Keynes, H. B.. Topological dynamics in coset transformation groups. Bull. Amer. Math. Soc. (N.S.) 72 (1966), 1033–1035.Google Scholar
Keynes, H. B.. A study of the proximal relation in coset transformation groups. Trans. Amer. Math. Soc. 128 (1967), 389–402.CrossRefGoogle Scholar
Khintchine, A. Y.. Eine Verschärfung des Poincaréschen ‘Wiederkehrsatzes’. Comput. Math. 1 (1934), 177–179.Google Scholar
Leibman, A.. Pointwise convergence of ergodic averages, for polynomial sequences of translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25 (2005), 201–213.CrossRefGoogle Scholar
Leibman, A.. Pointwise convergence of ergodic averages, for polynomial actions of ℤ d by translations on a nilmanifold. Ergod. Th. & Dynam. Sys. 25 (2005), 215–225.Google Scholar
Leibman, A.. Convergence of multiple ergodic averages along polynomials of several variables. Israel J. Math. 146 (2005), 303–315.Google Scholar
Leibman, A.. Rational sub-nilmanifolds of a compact nilmanifold. Ergod. Th. & Dynam. Sys. 26 (2006), 787–798.Google Scholar
Leibman, A.. Orbits on a nilmanifold under the action of a polynomial sequence of translations. Ergod. Th. & Dynam. Sys. 27 (2007), 1239–1252.Google Scholar
Leibman, A.. Orbit of the diagonal in the power of a nilmanifold. Trans. Amer. Math. Soc. 362 (2010), 1619–1658.Google Scholar
Leibman, A.. Nilsequences, nul-sequences, and the multiple correlation sequences. Ergod. Th. & Dynam. Sys. 31 (2015), 176–191.Google Scholar
McCutcheon, R.. Private communications, 2015.Google Scholar
McCutcheon, R. and Zhou, J.. D sets and IP rich sets in ℤ. Fund. Math. 233 (2016), 71–82.Google Scholar
Ziegler, T.. Universal characteristic factors and Furstenberg averages. J. Amer. Math. Soc. 20 (2007), 53–97.Google Scholar