Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-29T02:56:16.674Z Has data issue: false hasContentIssue false
  • English
  • Français

The set of points with Markovian symbolic dynamics for non-uniformly hyperbolic diffeomorphisms

Part of: Topological dynamics Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  04 November 2020

SNIR BEN OVADIA
SNIR BEN OVADIA*
Affiliation:
Weizmann Institute of Science, Department of Mathematics, Rehovot, 76100, Israel
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The papers [O. M. Sarig. Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc.26(2) (2013), 341–426] and [S. Ben Ovadia. Symbolic dynamics for non-uniformly hyperbolic diffeomorphisms of compact smooth manifolds. J. Mod. Dyn.13 (2018), 43–113] constructed symbolic dynamics for the restriction of 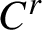$C^r$ diffeomorphisms to a set 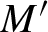$M'$ with full measure for all sufficiently hyperbolic ergodic invariant probability measures, but the set 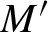$M'$ was not identified there. We improve the construction in a way that enables 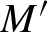$M'$ to be identified explicitly. One application is the coding of infinite conservative measures on the homoclinic classes of Rodriguez-Hertz et al. [Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys.306(1) (2011), 35–49].

Keywords

Markov partitionnon-uniform hyperbolicitysymbolic dynamics

MSC classification

Primary: 37B10: Symbolic dynamics 37D25: Nonuniformly hyperbolic systems (Lyapunov exponents, Pesin theory, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 11 , November 2021 , pp. 3244 - 3269
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s), 2020. Published by Cambridge University Press

References

Aaronson, J.. An Introduction to Infinite Ergodic Theory ( Mathematical Surveys and Monographs , 50 ). American Mathematical Society, Providence, RI, 1997.CrossRefGoogle Scholar
Adler, R. L. and Weiss, B.. Entropy, a complete metric invariant for automorphisms of the torus. Proc. Natl. Acad. Sci. USA 57 (1967), 1573–1576.CrossRefGoogle ScholarPubMed
Buzzi, J., Crovisier, S. and Sarig, O.. Measures of maximal entropy for surface diffeomorphisms. Preprint, 2018, arXiv:1811.02240.Google Scholar
Ben Ovadia, S.. Symbolic dynamics for non-uniformly hyperbolic diffeomorphisms of compact smooth manifolds. J. Mod. Dyn. 13 (2018), 43–113.CrossRefGoogle Scholar
Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms ( Lecture Notes in Mathematics , 470), revised edn. With a preface by David Ruelle. Ed. Chazottes, J.-R.. Springer, Berlin, 2008.CrossRefGoogle Scholar
Bowen, R. and Ruelle, D.. The ergodic theory of Axiom A flows. Invent. Math. 29(3) (1975), 181–202.CrossRefGoogle Scholar
Brin, M. and Stuck, G.. Introduction to Dynamical Systems. Cambridge University Press, Cambridge, 2002.CrossRefGoogle Scholar
Katok, A.. Lyapunov exponents, entropy and periodic orbits for diffeomorphisms. Publ. Math. Inst. Hautes Études Sci. 51 (1980), 137–173.CrossRefGoogle Scholar
Katok, A. and Hasselblatt, B.. Introduction to the Modern Theory of Dynamical Systems ( Encyclopedia of Mathematics and its Applications , 54). Cambridge University Press, Cambridge, 1995. With a supplementary chapter by Katok and Leonardo Mendoza.CrossRefGoogle Scholar
Katok, A. and Mendoza, L.. Dynamical systems with non-uniformly hyperbolic behavior. Supplement to Introduction to the Modern Theory of Dynamical Systems ( Encyclopedia of Mathematics and its Applications , 54). Cambridge University Press, Cambridge, 1995.CrossRefGoogle Scholar
Lima, Y.. Private communication.Google Scholar
Lima, Y.. Symbolic dynamics for nonuniformly hyperbolic systems. Preprint, 2019, arXiv:1910.11371.Google Scholar
Lima, Y.. Symbolic dynamics for one dimensional maps with nonuniform expansion. Ann. Inst. H. Poincaré Anal. Non Linéaire, 37(3) (2020), 727–755.CrossRefGoogle Scholar
Lima, Y. and Matheus, C.. Symbolic dynamics for non-uniformly hyperbolic surface maps with discontinuities. Ann. Sci. Éc. Norm. Supér. (4) 51(1) (2018), 1–38.CrossRefGoogle Scholar
Lima, Y. and Sarig, O. M.. Symbolic dynamics for three-dimensional flows with positive topological entropy. J. Eur. Math. Soc. (JEMS) 21(1) (2019), 199–256.CrossRefGoogle Scholar
Newhouse, S. E.. Hyperbolic limit sets. Trans. Amer. Math. Soc. 167 (1972), 125–150.CrossRefGoogle Scholar
Newhouse, S. E.. Continuity properties of entropy. Ann. of Math. (2) 129(2) (1989), 215–235.CrossRefGoogle Scholar
Pesin, J. B.. Families of invariant manifolds that correspond to nonzero characteristic exponents. Izv. Akad. Nauk SSSR Ser. Mat. 40(6) (1976), 1332–1379, 1440.Google Scholar
Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 268 (1990), 187–188.Google Scholar
Rodriguez Hertz, F., Rodriguez Hertz, M. A., Tahzibi, A. and Ures, R.. Uniqueness of SRB measures for transitive diffeomorphisms on surfaces. Comm. Math. Phys. 306(1) (2011), 35–49.CrossRefGoogle Scholar
Ruelle, D.. A measure associated with axiom-A attractors. Amer. J. Math. 98 (1976), 619–654.CrossRefGoogle Scholar
Ruelle, D.. Thermodynamic formalism. The Mathematical Structures of Equilibrium Statistical Mechanics (Cambridge Mathematical Library), 2nd edn. Cambridge University Press, Cambridge, 2004.Google Scholar
Sarig, O. M.. Symbolic dynamics for surface diffeomorphisms with positive entropy. J. Amer. Math. Soc. 26(2) (2013), 341–426.CrossRefGoogle Scholar
Sinaĭ, J. G.. Construction of Markov partitionings. Funktsional. Anal. i Priložhen. 2(3) (1968), 70–80 (Loose errata).Google Scholar
Sinaĭ, J. G.. Markov partitions and U-diffeomorphisms. Funktsional. Anal. i Priložhen. 2(1) (1968), 64–89.Google Scholar
Sinaĭ, J. G.. Gibbs measures in ergodic theory. Uspekhi Mat. Nauk 27(4(166)) (1972), 21–64.Google Scholar