Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T16:21:52.455Z Has data issue: false hasContentIssue false
  • English
  • Français

Semi-rigidity of horocycle flows over compact surfaces of variable negative curvature

Published online by Cambridge University Press:  19 September 2008

J. Feldman  and
D. Ornstein
J. Feldman
Affiliation:
Department of Mathematics, University of California, Berkeley, CA 94720, USA
D. Ornstein
Affiliation:
Department of Mathematics, Stanford University, Stanford, CA 94305, USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

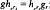Let g be the geodesic flow on the unit tangent bundle of a C3 compact surface of negative curvature. Let μ be the g-invariant measure of maximal entropy. Let h be a uniformly parametrized flow along the horocycle foliation, i.e., such a flow exists, leaves μ invariant, and is unique up to constant scaling of the parameter (Margulis). We show that any measure-theoretic conjugacy: (h, μ) → (h′, μ′) is a.e. of the form 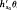θ, where θ is a homeomorphic conjugacy: g → g′. Furthermore, any homeomorphic conjugacy g → g′; must be a C1 diffeomorphism.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 7 , Issue 1 , March 1987 , pp. 49 - 72
Copyright
Copyright © Cambridge University Press 1987

References

REFERENCES

[A]Anosov, D. V.. Geodesic flows on closed Riemannian manifolds with negative curvature. Proc. Steklov Inst. of Math. # 90 (1967) (AMS translation, 1969).Google Scholar
[B]Berger, M. (Besse, A. L.). Manifolds All of Whose Geodesies Are Closed. Springer-Verlag, 1978.Google Scholar
[B-B]Ballman, W., Brin, M., Burns, K., Eberlein, P., Katok, A. & Osserman, R.. Manifolds of no npositive curvature. MSRI preprint, 1984.Google Scholar
[B-M]Bowen, R. & Marcus, B.. Unique ergodicity for horocyclic foliations. Israel J. Math. 43 (1977), 43–67.Google Scholar
[D]Dani, S. G.. Dynamics of the horospherical flow. Bull. Amer. Math. Soc. 3 (1980), 1037–1039.Google Scholar
[G-K]Guillemin, V. & Kazhdan, D.. Some inverse spectral results for negatively curved 2-manifolds. Topology 19 (1980), 301–302.Google Scholar
[H-P]Hirsch, M. & Pugh, C.. Smoothness of horocycle foliations. J. Diff. Geom. 10 (1975), 225–238.Google Scholar
[K]Katok, A.. Closed geodesies and conjugacy of geodesic flows. In preparation.Google Scholar
[L]Livčic, A. N.. Some homology properties of U-systems. Mat. Zametki 10 (1971), 555–564; Math. Notes 10 (1971), 758–763.Google Scholar
[M1]Marcus, B.. Unique ergodicity of the horocycle flow: variable negative curvature case. Israel J. Math. 21 (1975), 133–144.Google Scholar
[M2]Marcus, B.. Topological conjugacy of horocycle flows. Amer. J. Math. (1983), 623–632.Google Scholar
[Ma]Margulis, G. A.. Certain measures associated with U-flows on compact manifolds. Funct. Anal. Appl. 4 (1970), 55–67.Google Scholar
[P]Plante, J. F.. Anosov flows. Amer. Jour. Math. XCIV (1972), 729–754.Google Scholar
[R1]Ratner, M.. Rigidity of horocycle flows. Ann. Math. 115 (1982), 587–614.Google Scholar
[R2]Ratner, M.. Factors of horocycle flows. Ergod. Th. & Dynam. Sys. 2 (1982), 465–489.Google Scholar
[R3]Ratner, M.. Horocycle flows; joinings and rigidity of products. Ann. Math. 118 (1983), 277–313.Google Scholar
[R4]Ratner, M.. Ergodic theory in hyperbolic space. In Conference in Modern Analysis and Probability, Contemporary Math. 26. Amer. Math. Soc.Google Scholar
[R5]Ratner, M.. Rigidity of time changes for horocycle flows. To appear.Google Scholar
[Y-B]Yano, K. & Bochner, S.. Curvature and Betti Numbers. Princeton University Press, Princeton, NJ, 1953.Google Scholar