Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:05:28.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Ruelle operator with weakly contractive iterated function systems

Published online by Cambridge University Press:  31 August 2012

YUAN-LING YE
YUAN-LING YE*
Affiliation:
School of Mathematical Sciences, South China Normal University, Guangzhou 510631, People’s Republic of China (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

The Ruelle operator has been studied extensively both in dynamical systems and iterated function systems (IFSs). Given a weakly contractive IFS 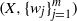$(X, \{w_j\}_{j=1}^m)$ and an associated family of positive continuous potential functions 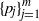$\{p_j\}_{j=1}^m$, a triple system 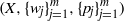$(X, \{w_j\}_{j=1}^m, \{p_j\}_{j=1}^m)$is set up. In this paper we study Ruelle operators associated with the triple systems. The paper presents an easily verified condition. Under this condition, the Ruelle operator theorem holds provided that the potential functions are Dini continuous. Under the same condition, the Ruelle operator is quasi-compact, and the iterations sequence of the Ruelle operator converges with a specific geometric rate, if the potential functions are Lipschitz continuous.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 4 , August 2013 , pp. 1265 - 1290
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Baladi, V.. Positive Transfer Operators and Decay of Correlations (Advanced Series in Nonlinear Dynamics, 16). World Scientific, Singapore, 2000.Google Scholar
[2]Baladi, V., Jiang, Y. P. and Lanford, O. E.. Transfer operators acting on Zygmund functions. Trans. Amer. Math. Soc. 348 (1996), 1599–1615.Google Scholar
[3]Barnsley, M. F., Demko, S. G., Elton, J. H. and Geronimo, J. S.. Invariant measures for Markov processes arising from iterated function systems with place-dependent probabilities. Ann. Inst. Henri Poincaré Probab. Stat. 24 (1988), 367–394.Google Scholar
[4]Bowen, R.. Equilibrium States and the Ergodic Theory of Anosov Diffeomorphisms (Lecture Notes in Mathematics, 470). Springer, Berlin, 1975.CrossRefGoogle Scholar
[5]Dunford, N. and Schwartz, J. T.. Linear Operators. Part I. Wiley Interscience, New York, NY, 1958.Google Scholar
[6]Fan, A. H.. A proof of the Ruelle operator theorem. Rev. Math. Phys. 7 (1995), 1241–1247.CrossRefGoogle Scholar
[7]Fan, A. H. and Jiang, Y. P.. On Ruelle–Perron–Frobenius operators I. Ruelle theorem. Comm. Math. Phys. 223 (2001), 125–141.Google Scholar
[8]Fan, A. H. and Jiang, Y. P.. On Ruelle–Perron–Frobenius operators II. Convergence speeds. Comm. Math. Phys. 223 (2001), 143–159.Google Scholar
[9]Fan, A. H. and Lau, K. S.. Iterated function system and Ruelle operator. J. Math. Anal. Appl. 231 (1999), 319–344.Google Scholar
[10]Hata, M.. On the structure of self-similar sets. Japan J. Appl. Math. 2 (1985), 381–414.Google Scholar
[11]Hennion, H.. Sur un théorèm spectral et son application aux noyaux lipchitziens. Proc. Amer. Math. Soc. 118 (1993), 627–634.Google Scholar
[12]Hutchinson, J. E.. Fractal and self-similarity. Indiana Univ. Math. J. 30 (1981), 713–747.Google Scholar
[13]Jiang, Y. P.. A proof of existence and simplicity of a maximal eigenvalue for Ruelle–Perron–Frobenius operators. Lett. Math. Phys. 48 (1999), 211–219.Google Scholar
[14]Jiang, Y. P. and Ye, Y. L.. Ruelle operator theorem for non-expansive systems. Ergod. Th. & Dynam. Sys. 30 (2010), 469–487.CrossRefGoogle Scholar
[15]Johansson, A. and Öberg, A.. Square summability of variations of $g$-functions and uniqueness of $g$-measures. Math. Res. Lett. 10 (2003), 587–601.Google Scholar
[16]Johansson, A., Öberg, A. and Pollicott, M.. Unique Bernoulli $g$-measures. J. Eur. Math. Soc. (JEMS) to appear.Google Scholar
[17]Lasota, A. and Yorke, J. A.. On the existence of invariant measures for piecewise monotonic transformations. Trans. Amer. Math. Soc. 186 (1973), 481–488.CrossRefGoogle Scholar
[18]Lau, K. S. and Ye, Y. L.. Ruelle operator with nonexpansive IFS. Studia Math. 148 (2001), 143–169.Google Scholar
[19]Liverani, C., Saussol, B. and Vaienti, S.. A probabilistic approach to intermittency. Ergod. Th. & Dynam. Sys. 19 (1999), 671–685.Google Scholar
[20]Mauldin, R. D. and Urbański, M.. Parabolic iterated function systems. Ergod. Th. & Dynam. Sys. 20 (2000), 1423–1448.Google Scholar
[21]Nussbaum, R. D.. The radius of the essential spectrum. Duke Math. J. 37 (1970), 473–478.Google Scholar
[22]Parry, W. and Pollicott, M.. Zeta functions and the periodic orbit structure of hyperbolic dynamics. Astérisque 187/188 (1990), 1–268.Google Scholar
[23]Pesin, Y. and Weiss, H.. The Multifractal analysis of Gibbs measures: motivation, mathematical foundation, and examples. Chaos 7 (1997), 89–106.Google Scholar
[24]Pomeau, Y. and Manneville, P.. Intermittent transition to turbulence in dissipative dynamical systems. Comm. Math. Phys. 74 (1980), 189–197.Google Scholar
[25]Prellberg, T. and Slawny, J.. Maps of intervals with indifferent fixed points: thermodynamic formalism and phase transitions. J. Stat. Phys. 66 (1991), 503–514.Google Scholar
[26]Ruelle, D.. Statical mechanics of a one-dimensional lattice gas. Comm. Math. Phys. 9 (1968), 267–278.Google Scholar
[27]Rugh, H. H.. Intermittency and regularized Fredholm determinants. Invent. Math. 135 (1999), 1–24.Google Scholar
[28]Urbański, M.. Parabolic Cantor sets. Fund. Math. 151 (1996), 241–277.Google Scholar
[29]Walters, P.. Ruelle’s operator theorem and $g$-measures. Trans. Amer. Math. Soc. 214 (1975), 375–387.Google Scholar
[30]Walters, P.. Convergence of the Ruelle operator for a function satisfying Bowen’s condition. Trans. Amer. Math. Soc. 353 (2001), 327–347.Google Scholar
[31]Walters, P.. A natural space of functions for the Ruelle operator theorem. Ergod. Th. & Dynam. Sys. 27 (2007), 1323–1348.Google Scholar
[32]Ye, Y. L.. Decay of correlations for weakly expansive dynamical systems. Nonlinearity 17 (2004), 1377–1391.Google Scholar
[33]Young, L. S.. Recurrence times and rates of mixing. Israel J. Math. 110 (1999), 153–188.CrossRefGoogle Scholar
[34]Yuri, M.. Multifractal analysis of weak Gibbs measures for intermittent systems. Comm. Math. Phys. 230 (2002), 365–388.Google Scholar