Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-26T19:53:15.332Z Has data issue: false hasContentIssue false
  • English
  • Français

Rokhlin dimension: duality, tracial properties, and crossed products

Part of: Selfadjoint operator algebras

Published online by Cambridge University Press:  18 October 2019

EUSEBIO GARDELLA ,
ILAN HIRSHBERG  and
LUIS SANTIAGO
EUSEBIO GARDELLA
Affiliation:
Mathematisches Institut, Fachbereich Mathematik und Informatik der Universität Münster, Einsteinstrasse 62, 48149Münster, Germany email [email protected]
ILAN HIRSHBERG
Affiliation:
Department of Mathematics, Ben-Gurion University of the Negev, Beer Sheva8410501, Israel email [email protected]
LUIS SANTIAGO
Affiliation:
Institute of Mathematics, University of Aberdeen, Fraser Noble Building, Aberdeen AB24 3UE, UK email [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We study compact group actions with finite Rokhlin dimension, particularly in relation to crossed products. For example, we characterize the duals of such actions, generalizing previous partial results for the Rokhlin property. As an application, we determine the ideal structure of their crossed products. Under the assumption of so-called commuting towers, we show that taking crossed products by such actions preserves a number of relevant classes of 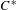$C^{\ast }$-algebras, including: 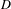$D$-absorbing 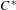$C^{\ast }$-algebras, where 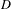$D$ is a strongly self-absorbing 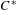$C^{\ast }$-algebra; stable 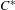$C^{\ast }$-algebras; 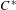$C^{\ast }$-algebras with finite nuclear dimension (or decomposition rank); 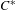$C^{\ast }$-algebras with finite stable rank (or real rank); and 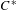$C^{\ast }$-algebras whose 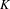$K$-theory is either trivial, rational, or $n$-divisible for 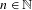$n\in \mathbb{N}$. The combination of nuclearity and the universal coefficient theorem (UCT) is also shown to be preserved by these actions. Some of these results are new even in the well-studied case of the Rokhlin property. Additionally, and under some technical assumptions, we show that finite Rokhlin dimension with commuting towers implies the (weak) tracial Rokhlin property. At the core of our arguments is a certain local approximation of the crossed product by a continuous 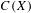$C(X)$-algebra with fibers that are stably isomorphic to the underlying algebra. The space 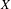$X$ is computed in some cases of interest, and we use its description to construct a 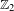$\mathbb{Z}_{2}$-action on a unital AF-algebra and on a unital Kirchberg algebra satisfying the UCT, whose Rokhlin dimensions with and without commuting towers are finite but do not agree.

Keywords

C∗ -algebraRokhlin dimensioncrossed products

MSC classification

Primary: 46L55: Noncommutative dynamical systems
Secondary: 46L35: Classifications of $C^*$-algebras 46L80: $K$-theory and operator algebras (including cyclic theory)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 41 , Issue 2 , February 2021 , pp. 408 - 460
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© The Author(s) 2019

References

Antoine, R., Bosa, J. and Perera, F.. The Cuntz semigroup of continuous fields. Indiana Univ. Math. J. 62 (2013), 1105–1131.CrossRefGoogle Scholar
Archey, D.. Crossed product $C^{\ast }$ -algebras by finite group actions with a generalized tracial Rokhlin property. PhD Thesis, University of Oregon, 2008. Retreived from ProQuest, LLC, Ann Arbor, MI.Google Scholar
Barlak, S. and Szabó, G.. Sequentially split ∗-homomorphisms between C∗ -algebras. Internat. J. Math. 27 (2016), 1650105, 48.CrossRefGoogle Scholar
Barlak, S. and Szabó, G.. Rokhlin actions of finite groups on UHF-absorbing C∗ -algebras. Trans. Amer. Math. Soc. 369 (2017), 833–859.CrossRefGoogle Scholar
Blackadar, B.. Symmetries of the CAR algebra. Ann. of Math. (2) 131 (1990), 589–623.CrossRefGoogle Scholar
Blackadar, B.. K-Theory for Operator Algebras (Mathematical Sciences Research Institute Publications, 5) , 2nd edn. Cambridge University Press, Cambridge, 1998.Google Scholar
Brown, L.. Continuity of actions of groups and semigroups on Banach spaces. J. Lond. Math. Soc. (2) 62 (2000), 107–116.CrossRefGoogle Scholar
Brown, N. and Ozawa, N.. C ∗ -algebras and Finite-Dimensional Approximations (Graduate Studies in Mathematics, 88) . American Mathematical Society, Providence, RI, 2008.CrossRefGoogle Scholar
Carrión, J.. Classification of a class of crossed product C ∗ -algebras associated with residually finite groups. J. Funct. Anal. 260 (2011), 2815–2825.CrossRefGoogle Scholar
Castillejos, J., Evington, S., Tikuisis, A., White, S. and Winter, W.. Nuclear dimension of simple $C^{\ast }$ -algebras, Preprint, 2019, arXiv:1901.05853.Google Scholar
Dadarlat, M.. Continuous fields of C ∗ -algebras over finite dimensional spaces. Adv. Math. 222 (2009), 1850–1881.CrossRefGoogle Scholar
Dadarlat, M.. Fiberwise KK -equivalence of continuous fields of C ∗ -algebras. J. K-Theory 3 (2009), 205–219.CrossRefGoogle Scholar
Dixmier, J.. C ∗ -Algebras (North-Holland Mathematical Library, 15) . North-Holland, Amsterdam, 1977. Translated from the French by Francis Jellett.Google Scholar
Elhage Hassan, N.. Rang réel de certaines extensions. Proc. Amer. Math. Soc. 123 (1995), 3067–3073.CrossRefGoogle Scholar
Elliott, G.. On the K-theory of the C ∗ -algebra generated by a projective representation of a torsion-free discrete abelian group. Operator Algebras and Group Representations, Vol. I (Neptun, 1980) (Monographs and Studies in Mathematics, 17) . Pitman, Boston, 1984, pp. 157–184.Google Scholar
Elliott, G., Gong, G., Lin, H. and Niu, Z.. On the classification of simple amenable $C^{\ast }$ -algebras with finite decomposition rank, II. Preprint, 2015. arXiv:1507.03437.CrossRefGoogle Scholar
Elliott, G. and Toms, A.. Regularity properties in the classification program for separable amenable C ∗ -algebras. Bull. Amer. Math. Soc. (N.S.) 45 (2008), 229–245.CrossRefGoogle Scholar
Gardella, E.. Compact group actions on C*-algebras: classification, non-classifiability, and crossed products and rigidity results for Lp-operator algebras. PhD Thesis, University of Oregon, 2015. Retreived from ProQuest, LLC, Ann Arbor, MI.Google Scholar
Gardella, E.. Crossed products by compact group actions with the Rokhlin property. J. Noncommut. Geom. 11 (2017), 1593–1626.CrossRefGoogle Scholar
Gardella, E.. Regularity properties and Rokhlin dimension for compact group actions. Houston J. Math. 43 (2017), 861–889.Google Scholar
Gardella, E.. Rokhlin dimension for compact group actions. Indiana Univ. Math. J. 66 (2017), 659–703.CrossRefGoogle Scholar
Gardella, E.. Circle actions on UHF-absorbing C ∗ -algebras. Houston J. Math. 44 (2018), 571–601.Google Scholar
Gardella, E.. Compact group actions with the Rokhlin property. Trans. Amer. Math. Soc. 371 (2019), 2837–2874.CrossRefGoogle Scholar
Gardella, E., Kalantar, M. and Lupini, M.. Model theory and Rokhlin dimension for compact quantum group actions. J. Noncommut. Geom. 13(2) (2019), 711–767.CrossRefGoogle Scholar
Gardella, E. and Lupini, M.. Conjugacy and cocycle conjugacy of automorphisms of 𝓞2 are not Borel. Münster J. Math. 9 (2016), 93–118.Google Scholar
Gardella, E. and Lupini, M.. Equivariant logic and applications to C ∗ -dynamics. Funct. Anal. 275(7) (2018), 1889–1942.CrossRefGoogle Scholar
Goldstein, P. and Izumi, M.. Quasi-free actions of finite groups on the Cuntz algebra 𝓞∞ . Tohoku Math. J. (2) 63 (2011), 729–749.CrossRefGoogle Scholar
Gootman, E., Lazar, A. and Peligrad, C.. Spectra for compact group actions. J. Operator Theory 31 (1994), 381–399.Google Scholar
Herman, R. and Jones, V.. Models of finite group actions. Math. Scand. 52 (1983), 312–320.CrossRefGoogle Scholar
Hirshberg, I., Kirchberg, E. and White, S.. Decomposable approximations of nuclear C ∗ -algebras. Adv. Math. 230(3) (2012), 1029–1039.CrossRefGoogle Scholar
Hirshberg, I. and Orovitz, J.. Tracially 𝓩-absorbing C ∗ -algebras. J. Funct. Anal. 265 (2013), 765–785.CrossRefGoogle Scholar
Hirshberg, I. and Phillips, N.. Rokhlin dimension: obstructions and permanence properties. Doc. Math. 20 (2015), 199–236.Google Scholar
Hirshberg, I., Rørdam, M. and Winter, W.. 𝓒0(X)-algebras, stability and strongly self-absorbing C ∗ -algebras. Math. Ann. 339 (2007), 695–732.CrossRefGoogle Scholar
Hirshberg, I., Szabó, G., Winter, W. and Wu, J.. Rokhlin dimension for flows. Comm. Math. Phys. 353 (2017), 253–316.CrossRefGoogle Scholar
Hirshberg, I. and Winter, W.. Rokhlin actions and self-absorbing C ∗ -algebras. Pacific J. Math. 233 (2007), 125–143.CrossRefGoogle Scholar
Hirshberg, I., Winter, W. and Zacharias, J.. Rokhlin dimension and C ∗ -dynamics. Comm. Math. Phys. 335 (2015), 637–670.CrossRefGoogle Scholar
Hjelmborg, J. and Rørdam, M.. On stability of C ∗ -algebras. J. Funct. Anal. 155(1) (1998), 153–170.CrossRefGoogle Scholar
Izumi, M.. Finite group actions on C ∗ -algebras with the Rohlin property. I. Duke Math. J. 122 (2004), 233–280.CrossRefGoogle Scholar
Jiang, X. and Su, H.. On a simple unital projectionless C ∗ -algebra. Amer. J. Math. 121 (1999), 359–413.Google Scholar
Kirchberg, E.. Central sequences in C ∗ -algebras and strongly purely infinite algebras. Operator Algebras: The Abel Symposium 2004 (Abel Symposia, 1) . Springer, Berlin, 2006, pp. 175–231.CrossRefGoogle Scholar
Kirchberg, E. and Rørdam, M.. Central sequence C-algebras and tensorial absorption of the Jiang–Su algebra. J. Reine Angew. Math. 695 (2014), 175–214.Google Scholar
Kirchberg, E. and Wassermann, S.. Operations on continuous bundles of C ∗ -algebras. Math. Ann. 303 (1995), 677–697.CrossRefGoogle Scholar
Kirchberg, E. and Wassermann, S.. Exact groups and continuous bundles of C ∗ -algebras. Math. Ann. 315 (1999), 169–203.CrossRefGoogle Scholar
Kirchberg, E. and Winter, W.. Covering dimension and quasidiagonality. Internat. J. Math. 15 (2004), 63–85.CrossRefGoogle Scholar
Kishimoto, A.. Simple crossed products of C ∗ -algebras by locally compact abelian groups. Yokohama Math. J. 28 (1980), 69–85.Google Scholar
Kishimoto, A.. Outer automorphisms and reduced crossed products of simple C ∗ -algebras. Comm. Math. Phys. 81 (1981), 429–435.CrossRefGoogle Scholar
Kishimoto, A.. A Rohlin property for one-parameter automorphism groups. Comm. Math. Phys. 179 (1996), 599–622.CrossRefGoogle Scholar
Lin, H.. An Introduction to the Classification of Amenable C ∗ -algebras. World Scientific, River Edge, NJ, 2001.Google Scholar
Matui, H. and Sato, Y.. 𝓩-stability of crossed products by strongly outer actions. Comm. Math. Phys. 314 (2012), 193–228.CrossRefGoogle Scholar
Milnor, J.. Construction of universal bundles. II. Ann. of Math. (2) 63 (1956), 430–436.CrossRefGoogle Scholar
Mostert, P.. Sections in principal fibre spaces. Duke Math. J. 23 (1956), 57–71.CrossRefGoogle Scholar
Nagisa, M., Osaka, H. and Phillips, N.. Ranks of algebras of continuous C ∗ -algebra valued functions. Canad. J. Math. 53 (2001), 979–1030.CrossRefGoogle Scholar
Osaka, H. and Phillips, N.. Crossed products by finite group actions with the Rokhlin property. Math. Z. 270 (2012), 19–42.CrossRefGoogle Scholar
Phillips, N.. Equivariant K-Theory and Freeness of Group Actions on C ∗ -Algebras (Lecture Notes in Mathematics, 1274) . Springer, Berlin, 1987.CrossRefGoogle Scholar
Phillips, N.. Every simple higher dimensional noncommutative torus is an AT algebra. Preprint, 2006 arXiv:0609.9783.Google Scholar
Phillips, N.. Freeness of actions of finite groups on C ∗ -algebras. Operator Structures and Dynamical Systems (Contemporary Mathematics, 503) . American Mathematical Society, Providence, RI, 2009, pp. 217–257.CrossRefGoogle Scholar
Phillips, N.. The tracial Rokhlin property for actions of finite groups on C ∗ -algebras. Amer. J. Math. 133 (2011), 581–636.CrossRefGoogle Scholar
Phillips, N.. Finite cyclic group actions with the tracial Rokhlin property. Trans. Amer. Math. Soc. 367 (2015), 5271–5300.CrossRefGoogle Scholar
Raeburn, I., Sinclair, A. and Williams, D.. Equivariant completely bounded operators. Pacific J. Math. 139 (1989), 155–194.CrossRefGoogle Scholar
Rieffel, M.. Applications of strong Morita equivalence to transformation group C ∗ -algebras. Operator Algebras and Applications, Part I (Kingston, ON, 1980) (Proceedings of Symposia in Pure Mathematics, 38) . American Mathematical Society, Providence, RI, 1982, pp. 299–310.CrossRefGoogle Scholar
Rørdam, M.. The stable and the real rank of 𝓩-absorbing C ∗ -algebras. Internat. J. Math. 15(10) (2004), 1065–1084.CrossRefGoogle Scholar
Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor. Duke Math. J. 55(2) (1987), 431–474.CrossRefGoogle Scholar
Santiago, L.. Crossed products by actions of finite groups with the Rokhlin property. Internat. J. Math. 26 (2015),1550042.CrossRefGoogle Scholar
Sato, Y. Trace spaces of simple nuclear $C^{\ast }$ -algebras with finite-dimensional extreme boundary. Preprint, 2012, arXiv:1209.3000.Google Scholar
Slawny, J.. On factor representations and the C ∗ -algebra of canonical commutation relations. Comm. Math. Phys. 24 (1972), 151–170.CrossRefGoogle Scholar
Sudo, T.. Stable rank of C ∗ -algebras of continuous fields. Tokyo J. Math. 28 (2005), 173–188.CrossRefGoogle Scholar
Thiel, H.. Ranks of operators in simple C*-algebras with stable rank one. Comm. Math. Phys. doi:10.1007/s00220-019-03491-8. Published online 1 July 2019.CrossRefGoogle Scholar
Thiel, H.. Inductive limits of semiprojective C ∗ -algebras. Adv. Math. 347 (2019), 597–618.CrossRefGoogle Scholar
Tikuisis, A., White, S. and Winter, W.. Quasidiagonality of nuclear C ∗ -algebras. Ann. of Math. (2) 185 (2017), 229–284.CrossRefGoogle Scholar
Toms, A., White, S. and Winter, W.. 𝓩-stability and finite dimensional tracial boundaries. Int. Math. Res. Not. IMRN 10 (2015), 2702–2727.Google Scholar
Toms, A. and Winter, W.. Strongly self-absorbing C ∗ -algebras. Trans. Amer. Math. Soc. 359 (2007), 3999–4029.CrossRefGoogle Scholar
Wang, Q.. Tracial Rokhlin property and non-commutative dimensions. PhD Thesis, Washington University in St. Louis, 2013. Retrieved from ProQuest LLC, Ann Arbor, MI.Google Scholar
Winter, W.. Strongly self-absorbing C ∗ -algebras are 𝓩-stable. J. Noncommut. Geom. 5 (2011), 253–264.CrossRefGoogle Scholar
Winter, W. and Zacharias, J.. The nuclear dimension of C ∗ -algebras. Adv. Math. 224(2) (2010), 461–498.CrossRefGoogle Scholar
Winter, W. and Zacharias, J.. Completely positive maps of order zero. Münster J. Math. 2 (2009), 311–324.Google Scholar