Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T04:07:38.429Z Has data issue: false hasContentIssue false
  • English
  • Français

Relative equilibrium states and class degree

Published online by Cambridge University Press:  22 June 2017

MAHSA ALLAHBAKHSHI ,
JOHN ANTONIOLI Open the ORCID record for JOHN ANTONIOLI [Opens in a new window]  and
JISANG YOO
MAHSA ALLAHBAKHSHI
Affiliation:
Universidad de Santiago de Chile, Alameda 3363, Santiago, Chile email [email protected]
JOHN ANTONIOLI
Affiliation:
University of Denver, 2199 S University Boulevard, Denver, CO 80208, USA email [email protected]
JISANG YOO
Affiliation:
Seoul National University, 1 Gwanak-ro, Daehak-dong, Gwanak-gu, Seoul, South Korea email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Given a factor code $\unicode[STIX]{x1D70B}$ from a shift of finite type $X$ onto a sofic shift $Y$, an ergodic measure $\unicode[STIX]{x1D708}$ on $Y$, and a function $V$ on 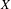$X$ with sufficient regularity, we prove an invariant upper bound on the number of ergodic measures on 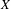$X$ which project to $\unicode[STIX]{x1D708}$ and maximize the measure pressure 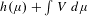$h(\unicode[STIX]{x1D707})+\int V\,d\unicode[STIX]{x1D707}$ among all measures in the fiber 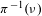$\unicode[STIX]{x1D70B}^{-1}(\unicode[STIX]{x1D708})$. If $\unicode[STIX]{x1D708}$ is fully supported, this bound is the class degree of $\unicode[STIX]{x1D70B}$. This generalizes a previous result for the special case of 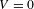$V=0$ and thus settles a conjecture raised by Allahbakhshi and Quas.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 4 , April 2019 , pp. 865 - 888
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Allahbakhshi, M., Hong, S. and Jung, U.. Structure of transition classes for factor codes on shifts of finite type. Ergod. Th. & Dynam. Sys. 35(8) (2015), 2353–2370.Google Scholar
Allahbakhshi, M. and Quas, A.. Class degree and relative maximal entropy. Trans. Amer. Math. Soc. 365(3) (2013), 1347–1368.Google Scholar
Antonioli, J.. Compensation functions for factors of shifts of finite type. Ergod. Th. & Dynam. Sys. 36(2) (2016), 375–389.Google Scholar
Bowen, R.. Symbolic Dynamics for Hyperbolic Systems (Lecture Notes in Mathematics, 318) . Springer, Berlin, 1975, pp. 51–58.Google Scholar
Ledrappier, F. and Walters, P.. A relativised variational principle for continuous transformations. J. Lond. Math. Soc. (2) 16(3) (1977), 568–576.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Parry, W.. Intrinsic Markov chains. Trans. Amer. Math. Soc. 112 (1964), 55–66.Google Scholar
Petersen, K., Quas, A. and Shin, S.. Measures of maximal relative entropy. Ergod. Th. & Dynam. Sys. 23(1) (2003), 207–223.Google Scholar
Ruelle, D.. Thermodynamic Formalism. Addison-Wesley, Reading, MA, 1978.Google Scholar
Sinai, Y.. Gibbs measures in ergodic theory. Uspekhi Mat. Nauk 27 (1972), 21–64.Google Scholar
Walters, P.. Relative pressure, relative equilibrium states, compensation functions and many-to-one codes between subshifts. Trans. Amer. Math. Soc. 296(1) (1986), 1–31.Google Scholar
Yoo, J.. Measures of maximal relative entropy with full support. Ergod. Th. & Dynam. Sys. 31(6) (2011), 1889–1899.Google Scholar
Yoo, J.. Multiplicity structure of preimages of invariant measures under finite-to-one factor maps. Trans. Amer. Math. Soc. to appear.Google Scholar