Article contents
Reduction of dynatomic curves
Published online by Cambridge University Press: 25 January 2018
Abstract
In this paper, we make partial progress on a function field version of the dynamical uniform boundedness conjecture for certain one-dimensional families 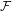 ${\mathcal{F}}$ of polynomial maps, such as the family
${\mathcal{F}}$ of polynomial maps, such as the family 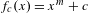 $f_{c}(x)=x^{m}+c$, where
$f_{c}(x)=x^{m}+c$, where 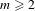 $m\geq 2$. We do this by making use of the dynatomic modular curves
$m\geq 2$. We do this by making use of the dynatomic modular curves 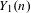 $Y_{1}(n)$ (respectively
$Y_{1}(n)$ (respectively 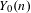 $Y_{0}(n)$) which parametrize maps
$Y_{0}(n)$) which parametrize maps 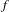 $f$ in
$f$ in 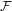 ${\mathcal{F}}$ together with a point (respectively orbit) of period
${\mathcal{F}}$ together with a point (respectively orbit) of period  $n$ for
$n$ for 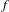 $f$. The key point in our strategy is to study the set of primes
$f$. The key point in our strategy is to study the set of primes 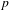 $p$ for which the reduction of
$p$ for which the reduction of 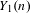 $Y_{1}(n)$ modulo
$Y_{1}(n)$ modulo 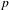 $p$ fails to be smooth or irreducible. Morton gave an algorithm to construct, for each
$p$ fails to be smooth or irreducible. Morton gave an algorithm to construct, for each  $n$, a discriminant
$n$, a discriminant 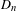 $D_{n}$ whose list of prime factors contains all the primes of bad reduction for
$D_{n}$ whose list of prime factors contains all the primes of bad reduction for 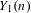 $Y_{1}(n)$. In this paper, we refine and strengthen Morton’s results. Specifically, we exhibit two criteria on a prime
$Y_{1}(n)$. In this paper, we refine and strengthen Morton’s results. Specifically, we exhibit two criteria on a prime 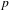 $p$ dividing
$p$ dividing 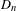 $D_{n}$: one guarantees that
$D_{n}$: one guarantees that 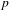 $p$ is in fact a prime of bad reduction for
$p$ is in fact a prime of bad reduction for 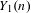 $Y_{1}(n)$, yet this same criterion implies that
$Y_{1}(n)$, yet this same criterion implies that 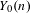 $Y_{0}(n)$ is geometrically irreducible. The other guarantees that the reduction of
$Y_{0}(n)$ is geometrically irreducible. The other guarantees that the reduction of 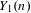 $Y_{1}(n)$ modulo
$Y_{1}(n)$ modulo 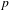 $p$ is actually smooth. As an application of the second criterion, we extend results of Morton, Flynn, Poonen, Schaefer, and Stoll by giving new examples of good reduction of
$p$ is actually smooth. As an application of the second criterion, we extend results of Morton, Flynn, Poonen, Schaefer, and Stoll by giving new examples of good reduction of 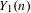 $Y_{1}(n)$ for several primes dividing
$Y_{1}(n)$ for several primes dividing 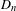 $D_{n}$ when
$D_{n}$ when 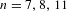 $n=7,8,11$, and
$n=7,8,11$, and 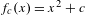 $f_{c}(x)=x^{2}+c$. The proofs involve a blend of arithmetic and complex dynamics, reduction theory for curves, ramification theory, and the combinatorics of the Mandelbrot set.
$f_{c}(x)=x^{2}+c$. The proofs involve a blend of arithmetic and complex dynamics, reduction theory for curves, ramification theory, and the combinatorics of the Mandelbrot set.
- Type
- Original Article
- Information
- Copyright
- © Cambridge University Press, 2018
References
- 3
- Cited by


