Hostname: page-component-6bf8c574d5-t27h7 Total loading time: 0 Render date: 2025-02-17T12:59:08.403Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrence on affine Grassmannians

Published online by Cambridge University Press:  05 April 2018

YVES BENOIST  and
CAROLINE BRUÈRE
YVES BENOIST
Affiliation:
Université Paris-Sud, Orsay 91405, France email [email protected], [email protected]
CAROLINE BRUÈRE
Affiliation:
Université Paris-Sud, Orsay 91405, France email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the action of the affine group 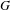$G$ of 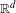$\mathbb{R}^{d}$ on the space 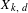$X_{k,\,d}$ of 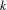$k$-dimensional affine subspaces. Given a compactly supported Zariski dense probability measure $\unicode[STIX]{x1D707}$ on 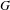$G$, we show that 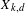$X_{k,d}$ supports a $\unicode[STIX]{x1D707}$-stationary measure $\unicode[STIX]{x1D708}$ if and only if the 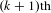$(k+1)\text{th}$ Lyapunov exponent of $\unicode[STIX]{x1D707}$ is strictly negative. In particular, when $\unicode[STIX]{x1D707}$ is symmetric, $\unicode[STIX]{x1D708}$ exists if and only if $2k\geq d$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 39 , Issue 12 , December 2019 , pp. 3207 - 3223
Copyright
© Cambridge University Press, 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Benoist, Y. and Quint, J.-F.. Mesures stationnaires et fermés invariants des espaces homogènes I. Ann. Math. 174 (2011), 1111–1162.Google Scholar
Benoist, Y. and Quint, J.-F.. Random walks on finite volume homogeneous spaces. Invent. Math. 187 (2012), 37–59.Google Scholar
Benoist, Y. and Quint, J.-F.. Random walks on projective spaces. Compos. Math. 150 (2014), 1579–1606.Google Scholar
Benoist, Y. and Quint, J.-F.. Random Walks on Reductive Groups. Springer, Berlin, 2016.Google Scholar
Bougerol, P., Babillot, M. and Élie, L.. The random difference equation x n = a n x n-1 + b n in the critical case. Ann. Probab. 25 (1997), 478–493.Google Scholar
Bougerol, P. and Picard, N.. Strict stationarity of generalized autoregressive processes. Ann. Probab. 20 (1992), 1714–1730.Google Scholar
Bourbaki, N.. Groupes et Algèbres de Lie. Springer, Berlin, 2006, Chs. 7 and 8.Google Scholar
Breiman, L.. Probability (Classics in Applied Mathematics, 7) . SIAM, Philadelphia, 1992.Google Scholar
Bruère, C.. Un critère de récurrence pour certains espaces homogènes. Preprint, 2016, arXiv:1607.05698, Bulletin de la SMF, to appear.Google Scholar
Eskin, A. and Margulis, G.. Recurrence properties of random walks on finite volume homogeneous spaces. Random Walks and Geometry. de Gruyter, Berlin, 2004, pp. 431–444.Google Scholar
Furstenberg, H.. Noncommuting random products. Trans. Amer. Math. Soc. 108 (1963), 377–428.Google Scholar
Goldsheid, I. and Margulis, G.. Lyapunov indices of a product of random matrices. Russian Math. Surveys 44 (1989), 11–81.Google Scholar
Guivarc’h, Y. and Raugi, A.. Frontière de Furstenberg, propriété de contraction et théorèmes de convergence. Z. Wahrscheinlichkeitsth. verw. Geb. 69 (1985), 187–242.Google Scholar
Ledrappier, F.. Quelques propriétés des exposants caractéristiques. Springer, Berlin, 1984, pp. 305–396.Google Scholar
Meyn, S. and Tweedie, R.. Markov Chain and Stochastic Stability. Springer, Berlin, 1993.Google Scholar
Oseledets, V.. A multiplicative ergodic theorem. Tr. Mosk. Mat. 19 (1968), 179–210.Google Scholar