No CrossRef data available.
Article contents
Quasi-adelic measures and equidistribution on 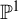 ${\mathbb P}^1$
${\mathbb P}^1$
Published online by Cambridge University Press: 01 August 2022
Abstract
Baker and Rumely, Favre, Rivera, and Letelier, and Chambert-Loir proved an important arithmetic equidistribution theorem for points of small height associated to an adelic measure. To broaden the scope in which arithmetic equidistribution may be employed, we generalize the notion of an adelic measure to that of a quasi-adelic measure and show that arithmetic equidistribution holds for quasi-adelic measures as well. We exhibit examples of non-adelic, quasi-adelic measures arising from the dynamics of quadratic rational maps. In fact, we show that the measures that arise in applications of arithmetic equidistribution theorems are typically not adelic. Finally, we motivate our definition of a quasi-adelic measure by relating it to a seemingly different problem in arithmetic dynamics arising from results of Call, Tate, and Silverman in the study of abelian varieties.
Keywords
MSC classification
- Type
- Original Article
- Information
- Copyright
- © The Author(s), 2022. Published by Cambridge University Press



