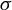1 Introduction
This article is concerned with dynamical systems with pure point spectrum. The dynamical systems in question consist of a continuous action of a locally compact abelian group on a compact metric space together with an invariant probability measure on the space. Pure point spectrum means that there exists an orthonormal basis of eigenfunctions. In a sense, such systems are the simplest possible dynamical systems. Their study is a most basic ingredient in the conceptual theory of dynamical systems as witnessed by such fundamental results as the Halmos–von Neumann theorem or the Furstenberg structure theorem. Accordingly, a variety of characterizations for pure point spectrum has been established over the decades.
Recent years have brought two new lines of interest in such systems. One line is given by a series of works which analyze such systems via (weak) notions of equicontinuity [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16–Reference Garcia-Ramos and Marcus19, Reference Huang, Li, Thouvenot, Xu and Ye22]. The main thrust of these works is to characterize pure point spectrum as well as various strengthened versions thereof (see also [Reference Fuhrmann, Gröger and Jaeger15, Reference Huang, Wang and Ye23, Reference Vershik40, Reference Yu41] for related work). The other line comes from the investigation of aperiodic order. Aperiodic order, also known as mathematical theory of quasicrystals, has emerged as fruitful field of (not only) mathematics over the last three decades; see, e.g., [Reference Baake and Grimm2] for a recent monograph and [Reference Baake and Moody5, Reference Kellendonk, Lenz and Savinien24] for recent collections of surveys. A key feature of aperiodic order is the occurrence of (pure) point diffraction. A central result in the mathematical treatment of aperiodic order gives that pure point diffraction can be understood as pure point spectrum of suitable associated dynamical systems. In fact, this result is the outcome of a cumulative effort of various people over the last decades [Reference Baake and Lenz4, Reference Dworkin12, Reference Gouéré21, Reference Lee, Moody and Solomyak26, Reference Lenz and Moody30, Reference Lenz and Strungaru32, Reference Schlottmann, Baake and Moody37].
A common feature of all these works is that their considerations share a flavor of almost periodicity. On an intuitive level this is not surprising. After all, pure point spectrum means that all spectral measures are pure point measures. This, in turn, is equivalent to the Fourier transforms of these measures being almost periodic [Reference Gil de Lamadrid and Argabright20, Reference Moody, Strungaru, Baake and Grimm35]. In this way, almost periodicity properties of functions and their averages come into play in a very natural way.
However, what is lacking is a description of pure point spectrum via almost periodicity properties of the points of the dynamical system. The goal of this article it to provide such a characterization and to study some of its consequences.
In order to do so, we introduce for points in dynamical systems the concepts of mean almost periodicity, Besicovitch almost periodicity, Weyl almost periodicity, weak almost periodicity and Bohr almost periodicity, respectively.
After the discussion of the necessary background in §2, our first achievement is Theorem 3.8 in §3. This theorem says that a system has pure point spectrum if and only if every (or even just one) generic point is mean almost periodic. If the dynamical system is ergodic this is then equivalent to almost all points being mean almost periodic.
As for mean almost periodicity of points, in turn various characterizations are discussed in §3. One of them proceeds via averages of distance between the orbit of the point and a shifted orbit. Another characterizes mean almost periodicity of a point via almost periodicity properties of the sampling of continuous functions along the orbit of this point. In this way, we have a rather complete and clear picture of the meaning of mean almost periodic points for general dynamical systems.
This picture ties in with various earlier results. In the case where the group is just the integers, a related characterization via sampling of bounded measurable function is given in [Reference Bellow and Losert7] for measurable dynamical systems. In the more specific situation of subshifts over a finite alphabet, there is also a characterization of pure point spectrum via the so-called Besicovitch–Hamming almost periodicity of almost all configurations [Reference Vershik40, Lemma 5]. For constant length substitutions, the equivalence between mean almost periodicity and pure point spectrum was proved in [Reference Queffélec36, Lemma VI.25]. In the particular case of point processes in
![]() $\mathbb {R}^d$
, these results have been established in [Reference Gouéré21, Theorem 4.4]. Moreover, we point out a companion article [Reference Baake and Lenz3
Reference Akin and Glasner1] dealing with fundamental issues in aperiodic order via almost periodicity of measures. As an application, it treats the situation of a special dynamical system, namely translation bounded measures dynamical systems. These systems are particularly relevant to aperiodic order. In these systems, the points are measures and this allows one to work with almost periodicity properties of measures. Of course, this approach it not available for general dynamical systems.
$\mathbb {R}^d$
, these results have been established in [Reference Gouéré21, Theorem 4.4]. Moreover, we point out a companion article [Reference Baake and Lenz3
Reference Akin and Glasner1] dealing with fundamental issues in aperiodic order via almost periodicity of measures. As an application, it treats the situation of a special dynamical system, namely translation bounded measures dynamical systems. These systems are particularly relevant to aperiodic order. In these systems, the points are measures and this allows one to work with almost periodicity properties of measures. Of course, this approach it not available for general dynamical systems.
In terms of methods it should be emphasized that our proof of Theorem 3.8 is completely different from those given in [Reference Bellow and Losert7, Reference Lenz, Spindeler and Strungaru31, Reference Vershik40]. It relies on the characterization of pure point spectrum by Bohr almost periodicity of an averaged metric obtained recently in [Reference Lenz29].
In §4, we then introduce Besicovitch almost periodic points. Although the condition of Besicovitch almost periodicity is strictly stronger than mean almost periodicity, we can still show that an ergodic dynamical system has pure point spectrum if and only if almost all points are Besicovitch almost periodic and this holds if and only if there exists one generic Besicovitch almost periodic point (Theorem 4.7). In this respect the difference between mean and Besicovitch almost periodicity is not too large. The advantage of Besicovitch almost periodic points is that they allow for averaging with characters. In particular, it is possible to compute the eigenfunctions via the Besicovitch almost periodic points (Theorem 4.7). In fact, the complete spectral theory of the dynamical system can be directly computed from any single typical Besicovitch almost periodic point (Theorem 4.4).
In §5, we introduce Weyl almost periodic points. Weyl almost periodicity of a point is substantially stronger than Besicovitch almost periodicity. In fact, a point is Weyl almost periodic if and only if its orbit closure is uniquely ergodic and has pure point spectrum with continuous eigenfunctions (Theorem 5.5). In this case, all points in the orbit closure are Weyl almost periodic (Lemma 5.3). To put these results in perspective, we note that [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16] showed that a dynamical system is mean equicontinuous if and only if it is uniquely ergodic with pure point spectrum and continuous eigenvalues. Hence, a point is Weyl almost periodic if and only if its orbit closure is mean equicontinuous. Thus, our results can be understood to provide a natural pointwise counterpart to the results of [Reference Fuhrmann, Gröger and Lenz16].
In §6, we investigate two special classes of Weyl almost periodic points, namely Bohr and weakly almost periodic points, respectively. This allows us to characterize Bohr and weakly almost periodic dynamical systems. In particular, we reprove a main result of [Reference Lenz and Strungaru33]. An application of our results to aperiodic order is given in §7. This includes an alternative proof for the main results on measure dynamical systems contained in [Reference Lenz, Spindeler and Strungaru31].
Our article gives a comprehensive treatment of most relevant concepts of almost periodicity in the context of pure point spectrum. Some parts of our considerations allow for simple abstractions. As this may be of value for further investigations, we include a brief discussion of some basic results in §8.
It seems that Besicovitch almost periodicity is not well known (for groups other than
![]() $\mathbb {R}$
) and there is also some ambiguity in the way it is defined. For this reason, we include some appendices discussing the almost periodicity properties needed in this article as well as basic properties of the class of continuous functions with these almost periodicity properties.
$\mathbb {R}$
) and there is also some ambiguity in the way it is defined. For this reason, we include some appendices discussing the almost periodicity properties needed in this article as well as basic properties of the class of continuous functions with these almost periodicity properties.
2 Background on dynamical systems, pure point spectrum and the upper mean
In this section, we review the necessary concepts from dynamical systems and introduce the upper mean
![]() $\overline {M}$
, which is crucial for our subsequent considerations.
$\overline {M}$
, which is crucial for our subsequent considerations.
Throughout the paper, we denote the set of continuous complex-valued functions on the topological space Y by
![]() $C(Y)$
.
$C(Y)$
.
We consider a compact metric space X equipped with a continuous action
of a locally compact,
![]() $\sigma $
-compact, abelian group G. We then call
$\sigma $
-compact, abelian group G. We then call
![]() $(X,G)$
a dynamical system (over the space X). Often, we will also be given a probability measure m on X, which is invariant under the action of G. We then call
$(X,G)$
a dynamical system (over the space X). Often, we will also be given a probability measure m on X, which is invariant under the action of G. We then call
![]() $(X,G,m)$
a dynamical system as well. We write
$(X,G,m)$
a dynamical system as well. We write
![]() $tx$
instead of
$tx$
instead of
![]() $\alpha _t (x)$
for
$\alpha _t (x)$
for
![]() $t\in G$
and
$t\in G$
and
![]() $x\in X$
. The composition on G itself is written additively and the neutral element of G is denoted as e. We fix a Haar measure on G, which is unique up to multiplication by a positive constant. The Haar measure of a measurable subset
$x\in X$
. The composition on G itself is written additively and the neutral element of G is denoted as e. We fix a Haar measure on G, which is unique up to multiplication by a positive constant. The Haar measure of a measurable subset
![]() $A\subset G$
is denoted by
$A\subset G$
is denoted by
![]() $|A|$
and the integral of an integrable function f on G by
$|A|$
and the integral of an integrable function f on G by
![]() $\int f(t)\,d t$
.
$\int f(t)\,d t$
.
Whenever a dynamical system
![]() $(X,G)$
is given, we furthermore make use of:
$(X,G)$
is given, we furthermore make use of:
-
• a metric d on X which generates the topology;
-
• a Følner sequence
 $(B_n)$
in G, that is, each
$(B_n)$
in G, that is, each
 $B_n$
is an open relatively compact subset of G and for all
$B_n$
is an open relatively compact subset of G and for all $$ \begin{align*} \frac{|(B_n \setminus (t+B_n)) \cup ((t+B_n)\setminus B_n)|}{|B_n|} \to 0,\quad n\to \infty, \end{align*} $$
$$ \begin{align*} \frac{|(B_n \setminus (t+B_n)) \cup ((t+B_n)\setminus B_n)|}{|B_n|} \to 0,\quad n\to \infty, \end{align*} $$
 $t\in G$
.
$t\in G$
.
Note that a Følner sequence exists in a locally compact abelian group G if an only if G is
![]() $\sigma $
-compact [Reference Spindeler and Strungaru39, Proposition B6]. For this reason, we always assume that G is
$\sigma $
-compact [Reference Spindeler and Strungaru39, Proposition B6]. For this reason, we always assume that G is
![]() $\sigma $
-compact.
$\sigma $
-compact.
The orbit of x is given by
![]() $Gx:=\{tx : t\in G\}$
and the orbit closure
$Gx:=\{tx : t\in G\}$
and the orbit closure
![]() $\overline {Gx}$
is the closure of the orbit. If the orbit closure of
$\overline {Gx}$
is the closure of the orbit. If the orbit closure of
![]() $x\in X$
agrees with X, the element x is called transitive. If every
$x\in X$
agrees with X, the element x is called transitive. If every
![]() $x\in X$
is transitive the dynamical system is called minimal. The dynamical system
$x\in X$
is transitive the dynamical system is called minimal. The dynamical system
![]() $(X,G)$
is called uniquely ergodic if there exists only one invariant probability measure on X. We then denote this measure by m and call
$(X,G)$
is called uniquely ergodic if there exists only one invariant probability measure on X. We then denote this measure by m and call
![]() $(X,G,m)$
uniquely ergodic as well.
$(X,G,m)$
uniquely ergodic as well.
The dynamical system
![]() $(X,G,m)$
is ergodic if any invariant measurable subset A of G satisfies
$(X,G,m)$
is ergodic if any invariant measurable subset A of G satisfies
![]() $m(A)=1$
or
$m(A)=1$
or
![]() $m(A) =0$
. If
$m(A) =0$
. If
![]() $(X,G,m)$
is ergodic, any Følner sequence has a subsequence
$(X,G,m)$
is ergodic, any Følner sequence has a subsequence
![]() $(B_n)$
for which Birkhoff’s ergodic theorem holds, that is,
$(B_n)$
for which Birkhoff’s ergodic theorem holds, that is,
 $$ \begin{align*} \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(tx)\,d t = \int_X f \,d m \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(tx)\,d t = \int_X f \,d m \end{align*} $$
is valid for almost every
![]() $x\in X$
whenever
$x\in X$
whenever
![]() $f: X\longrightarrow \mathbb {C}$
integrable [Reference Linderstauss34].
$f: X\longrightarrow \mathbb {C}$
integrable [Reference Linderstauss34].
Whenever a dynamical system
![]() $(X,G,m)$
and a Følner sequence
$(X,G,m)$
and a Følner sequence
![]() $(B_n)$
is given, a point
$(B_n)$
is given, a point
![]() $y\in X$
is called m-generic with respect to the Følner sequence if
$y\in X$
is called m-generic with respect to the Følner sequence if
 $$ \begin{align*} \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(ty)\,d t = \int_X f(x) \,d m(x) \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(ty)\,d t = \int_X f(x) \,d m(x) \end{align*} $$
holds for any continuous
![]() $f : X\longrightarrow \mathbb {C}$
. If the measure m and the sequence
$f : X\longrightarrow \mathbb {C}$
. If the measure m and the sequence
![]() $(B_n)$
are clear from the context, we just speak about generic points. Generic points play a key role in our subsequent considerations as they determine the measure and, in this sense, the whole dynamical system. As is well known (and not hard to see), the set of generic points is measurable and invariant under the group action. Moreover, the set of generic points has full measure if
$(B_n)$
are clear from the context, we just speak about generic points. Generic points play a key role in our subsequent considerations as they determine the measure and, in this sense, the whole dynamical system. As is well known (and not hard to see), the set of generic points is measurable and invariant under the group action. Moreover, the set of generic points has full measure if
![]() $(X,G,m)$
is ergodic and Birkhoff’s ergodic theorem holds along the underlying Følner sequence. Although we do not need it here, it is instructive for our subsequent considerations to note that a converse of sorts holds as well: if m is an invariant probability measure such that the set of m-generic points with respect to some Følner sequence has full measure, then
$(X,G,m)$
is ergodic and Birkhoff’s ergodic theorem holds along the underlying Følner sequence. Although we do not need it here, it is instructive for our subsequent considerations to note that a converse of sorts holds as well: if m is an invariant probability measure such that the set of m-generic points with respect to some Følner sequence has full measure, then
![]() $(X,G,m)$
is ergodic. Thus, ergodicity is a necessary and sufficient condition for having an ample supply of generic points at ones disposal. This is ultimately the reason that most (but not all) of our theorems in the following deal with ergodic systems.
$(X,G,m)$
is ergodic. Thus, ergodicity is a necessary and sufficient condition for having an ample supply of generic points at ones disposal. This is ultimately the reason that most (but not all) of our theorems in the following deal with ergodic systems.
A dynamical system
![]() $(X,G,m)$
is said to have pure point spectrum if there exists an orthonormal basis of
$(X,G,m)$
is said to have pure point spectrum if there exists an orthonormal basis of
![]() $L^2 (X,m)$
consisting of eigenfunctions. Here, an
$L^2 (X,m)$
consisting of eigenfunctions. Here, an
![]() $f\in L^2 (X,m)$
with
$f\in L^2 (X,m)$
with
![]() $f\neq 0$
is called an eigenfunction if for any
$f\neq 0$
is called an eigenfunction if for any
![]() $t\in G$
there exist a
$t\in G$
there exist a
![]() $\xi (t)\in \mathbb {C}$
with
$\xi (t)\in \mathbb {C}$
with
in the sense of
![]() $L^2 (X,m)$
functions. In this case, each
$L^2 (X,m)$
functions. In this case, each
![]() $\xi (t)$
belongs to the group
$\xi (t)$
belongs to the group
and the map
can easily be seen to be a continuous group homomorphism. It is called eigenvalue. Clearly, eigenfunctions to different eigenvalues are orthogonal. As X is compact and metrizable,
![]() $L^2 (X,m)$
is separable. Hence, the set of eigenvalues is (at most) countable. We denote by
$L^2 (X,m)$
is separable. Hence, the set of eigenvalues is (at most) countable. We denote by
![]() $P_\xi $
the projection onto the eigenspace of
$P_\xi $
the projection onto the eigenspace of
![]() $\xi $
if
$\xi $
if
![]() $\xi $
is an eigenvalue and set
$\xi $
is an eigenvalue and set
![]() $P_\xi =0$
if
$P_\xi =0$
if
![]() $\xi $
is not an eigenvalue. The set of eigenvalues of
$\xi $
is not an eigenvalue. The set of eigenvalues of
![]() $(X,G,m)$
will be denoted by
$(X,G,m)$
will be denoted by
![]() $\mathrm {Eig}(X,G,m)$
. As is well known the set of eigenvalues is a group if
$\mathrm {Eig}(X,G,m)$
. As is well known the set of eigenvalues is a group if
![]() $(X,G,m)$
is ergodic.
$(X,G,m)$
is ergodic.
For our further discussion, we also rely on some concepts defined purely with respect to G (that is, they do not need the dynamical system). Let
![]() $(B_n)$
be a Følner sequence, and let
$(B_n)$
be a Følner sequence, and let
![]() $B(G)$
denote the set of bounded measurable real-valued functions on G. Then, we define the associated upper mean via
$B(G)$
denote the set of bounded measurable real-valued functions on G. Then, we define the associated upper mean via
 $$ \begin{align*} \overline{M}_{(B_n)} : B(G) \longrightarrow [0,\infty),\quad \overline{M}_{(B_n)} (h) :=\limsup_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} h(s)\,d s. \end{align*} $$
$$ \begin{align*} \overline{M}_{(B_n)} : B(G) \longrightarrow [0,\infty),\quad \overline{M}_{(B_n)} (h) :=\limsup_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} h(s)\,d s. \end{align*} $$
If the Følner sequence is clear from the context we drop the subscript
![]() $(B_n)$
. Clearly,
$(B_n)$
. Clearly,
![]() $\overline {M}$
gives rise to seminorm on the space of bounded measurable functions on G via
$\overline {M}$
gives rise to seminorm on the space of bounded measurable functions on G via
![]() $f\mapsto \overline {M}(|f|)$
.
$f\mapsto \overline {M}(|f|)$
.
A subset A of G is called relatively dense if there exists a compact set
![]() $K\subset G$
with
$K\subset G$
with
A continuous bounded
![]() $f : G\longrightarrow \mathbb {C}$
is called Bohr almost periodic if for any
$f : G\longrightarrow \mathbb {C}$
is called Bohr almost periodic if for any
![]() $\varepsilon>0$
the set of
$\varepsilon>0$
the set of
![]() $t\in G$
with
$t\in G$
with
is relatively dense. Here, the supremum norm
![]() $\|\cdot \|_\infty $
for bounded complex-valued functions on G is defined via
$\|\cdot \|_\infty $
for bounded complex-valued functions on G is defined via
![]() $\|f\|_\infty =\sup _{s\in G} |f(s)|$
.
$\|f\|_\infty =\sup _{s\in G} |f(s)|$
.
3 Mean almost periodic points and pure point spectrum
In this section, we introduce and study mean almost periodic points. The main result of this section then provides a characterization of pure point spectrum via mean almost periodicity of points.
Whenever
![]() $(X,G)$
is a dynamical system with metric d and
$(X,G)$
is a dynamical system with metric d and
![]() $(B_n)$
is a Følner sequence, we define
$(B_n)$
is a Følner sequence, we define
Clearly, D is a pseudometric. Moreover, the Følner condition on
![]() $(B_n)$
easily gives that D is invariant, that is, satisfies
$(B_n)$
easily gives that D is invariant, that is, satisfies
![]() $D(tx, ty) = D(x,y)$
for all
$D(tx, ty) = D(x,y)$
for all
![]() $x,y\in X$
and
$x,y\in X$
and
![]() $t\in G$
. Furthermore, for each
$t\in G$
. Furthermore, for each
![]() $x\in X$
the function
$x\in X$
the function
![]() $G\to [0,\infty )$
,
$G\to [0,\infty )$
,
![]() $t\mapsto D(x,tx)$
, is uniformly continuous. Indeed, continuity at
$t\mapsto D(x,tx)$
, is uniformly continuous. Indeed, continuity at
![]() $t=0$
is easily seen from the definition. Moreover, due to the invariance and the pseudometric properties we infer
$t=0$
is easily seen from the definition. Moreover, due to the invariance and the pseudometric properties we infer
When combined with continuity at
![]() $t =0$
, this gives uniform continuity. We refer to D as the averaged metric on X associated to d and
$t =0$
, this gives uniform continuity. We refer to D as the averaged metric on X associated to d and
![]() $(B_n)$
.
$(B_n)$
.
Definition 3.1. (Mean almost periodic points)
Let
![]() $(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
$(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
![]() $(B_n)$
be a Følner sequence and let D be the associated averaged metric. Then, a point
$(B_n)$
be a Følner sequence and let D be the associated averaged metric. Then, a point
![]() $x\in X$
is called mean almost periodic with respect to d and
$x\in X$
is called mean almost periodic with respect to d and
![]() $(B_n)$
if for every
$(B_n)$
if for every
![]() $\varepsilon>0$
the set
$\varepsilon>0$
the set
is relatively dense.
Remark. Almost periodicity properties with respect to
![]() $\overline {M}$
are often connected with the name of Besicovitch. We use this for a strengthened version to be introduced in the following. Here we stick to the term ‘mean’ as this seems to be the common term within the study of equicontinuity properties in recent years (see, e.g., [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16, Reference Garcia-Ramos and Marcus19] as well as the discussion in Appendix C).
$\overline {M}$
are often connected with the name of Besicovitch. We use this for a strengthened version to be introduced in the following. Here we stick to the term ‘mean’ as this seems to be the common term within the study of equicontinuity properties in recent years (see, e.g., [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16, Reference Garcia-Ramos and Marcus19] as well as the discussion in Appendix C).
By definition, mean almost periodicity depends on the chosen Følner sequence. In our subsequent discussion of mean almost periodic points, however, we often refrain from explicitly referring to the Følner sequence
![]() $(B_n)$
if it is clear from the context which sequence is involved.
$(B_n)$
if it is clear from the context which sequence is involved.
Lemma 3.2. Let
![]() $(X,G)$
be a dynamical system and let d be a metric on X generating the topology. An
$(X,G)$
be a dynamical system and let d be a metric on X generating the topology. An
![]() $x\in X$
is mean almost periodic if and only if the function
$x\in X$
is mean almost periodic if and only if the function
![]() $G\ni t\mapsto D(x,tx)\in \mathbb {R}$
is Bohr almost periodic.
$G\ni t\mapsto D(x,tx)\in \mathbb {R}$
is Bohr almost periodic.
Proof. Define f on G via
![]() $f(t) := D(x,tx)$
. We have already noted that the function f is uniformly continuous. Clearly, Bohr almost periodicity of f implies that x is mean almost periodic (as
$f(t) := D(x,tx)$
. We have already noted that the function f is uniformly continuous. Clearly, Bohr almost periodicity of f implies that x is mean almost periodic (as
![]() $f(0) =0$
). Conversely,
$f(0) =0$
). Conversely,
![]() $(\clubsuit )$
gives
$(\clubsuit )$
gives
![]() $|f(t +s) - f(s)| \leq f(t)$
for all
$|f(t +s) - f(s)| \leq f(t)$
for all
![]() $s,t\in G$
and mean almost periodicity of x implies Bohr almost periodicity of f.
$s,t\in G$
and mean almost periodicity of x implies Bohr almost periodicity of f.
Our next aim is to discuss independence of this definition from the metric and to provide an alternative way of defining mean almost periodicity via density of superlevel sets. The proofs of the corresponding statements are not difficult and rather close to each other. They rely on some simple facts stated in the next proposition. We denote the characteristic function of a set
![]() $A\subset G$
by
$A\subset G$
by
![]() $1_A$
(that is,
$1_A$
(that is,
![]() $1_A (x) = 1$
for
$1_A (x) = 1$
for
![]() $x\in A$
and
$x\in A$
and
![]() $1_A (x) =0$
for
$1_A (x) =0$
for
![]() $x\notin A$
).
$x\notin A$
).
Proposition 3.3. Let
![]() $f : G\longrightarrow [0,1]$
be given. Then, for any
$f : G\longrightarrow [0,1]$
be given. Then, for any
![]() $\delta>0$
the following estimates hold for the set
$\delta>0$
the following estimates hold for the set
![]() $A(f,\delta ):=\{s\in G : f(s) \geq \delta \}$
:
$A(f,\delta ):=\{s\in G : f(s) \geq \delta \}$
:
-
(a)
 $\overline {M}( 1_{A(f,\delta )}) \leq {1}/{\delta } \; \overline {M}(f)$
;
$\overline {M}( 1_{A(f,\delta )}) \leq {1}/{\delta } \; \overline {M}(f)$
; -
(b)
 $\overline {M}(f) \leq M(1_{A(f,\delta )}) + \delta .$
$\overline {M}(f) \leq M(1_{A(f,\delta )}) + \delta .$
Proof
-
(a) We clearly have
 $ 1_{\{s\in G : f(s) \geq \delta \}} \leq {1}/{\delta } f$
. This easily gives (a).
$ 1_{\{s\in G : f(s) \geq \delta \}} \leq {1}/{\delta } f$
. This easily gives (a). -
(b) We compute
This finishes the proof. $$ \begin{align*} \overline{M}(f) \leq \overline{M}( f \cdot 1_{\{s\in G : f(s) \geq \delta\}}) +\overline{M}( f\cdot 1_{\{s\in G : f(s) < \delta\}}) \leq \overline{M}( 1_{\{s\in G : f(s) \geq \delta\}}) + \delta.\end{align*} $$
$$ \begin{align*} \overline{M}(f) \leq \overline{M}( f \cdot 1_{\{s\in G : f(s) \geq \delta\}}) +\overline{M}( f\cdot 1_{\{s\in G : f(s) < \delta\}}) \leq \overline{M}( 1_{\{s\in G : f(s) \geq \delta\}}) + \delta.\end{align*} $$
Lemma 3.4. (Independence of the metric)
Let
![]() $(X,G)$
be a dynamical system with metrizable X and let
$(X,G)$
be a dynamical system with metrizable X and let
![]() $(B_n)$
be a Følner sequence on G. Then, mean almost periodicity of an
$(B_n)$
be a Følner sequence on G. Then, mean almost periodicity of an
![]() $x\in X$
does not depend on the chosen metric (provided it generates the topology).
$x\in X$
does not depend on the chosen metric (provided it generates the topology).
Proof. Let
![]() $e,d$
be two metrics on X, which generate the topology. For
$e,d$
be two metrics on X, which generate the topology. For
![]() $x\in X$
and
$x\in X$
and
![]() $t\in G$
we define the functions
$t\in G$
we define the functions
![]() $d_{t,x}$
and
$d_{t,x}$
and
![]() $e_{t,x}$
on G via
$e_{t,x}$
on G via
![]() $d_{t,x}(s) = d(sx,tsx)$
and
$d_{t,x}(s) = d(sx,tsx)$
and
![]() $e_{t,x}(s) = e(sx,tsx)$
, respectively. We show that for any
$e_{t,x}(s) = e(sx,tsx)$
, respectively. We show that for any
![]() $\varepsilon>0$
there exists a
$\varepsilon>0$
there exists a
![]() $\delta>0$
such that for any
$\delta>0$
such that for any
![]() $t\in G$
and
$t\in G$
and
![]() $x\in X$
we have
$x\in X$
we have
whenever
![]() $\overline {M}(e_{t,x}) < \delta $
holds. The statement with the roles of e and d reversed can be shown analogously and taken together these two statements prove the lemma.
$\overline {M}(e_{t,x}) < \delta $
holds. The statement with the roles of e and d reversed can be shown analogously and taken together these two statements prove the lemma.
Without loss of generality we assume
![]() $d,e\leq 1$
.
$d,e\leq 1$
.
Let
![]() $\varepsilon>0$
be given. Choose
$\varepsilon>0$
be given. Choose
![]() $\delta '>0$
with
$\delta '>0$
with
![]() $d(z,y) < {\varepsilon }/{2}$
whenever
$d(z,y) < {\varepsilon }/{2}$
whenever
![]() $e(z,y) < \delta '$
. Set
$e(z,y) < \delta '$
. Set
If
![]() $\overline {M}(e_{t,x}) < \delta $
, then Proposition 3.3(a) gives
$\overline {M}(e_{t,x}) < \delta $
, then Proposition 3.3(a) gives
Furthermore, we note that, by the definition of
![]() $\delta '$
, we have
$\delta '$
, we have
Given this we can now estimate
This is the desired statement.
By the previous lemma mean almost periodicity of a point is independent of the underlying metric. Hence, we can (and will) from now on refrain from specifying a metric when talking about mean almost periodicity.
We define the upper density of a subset
![]() $A\subset G$
via
$A\subset G$
via
Lemma 3.5. (Mean almost periodicity via density of superlevel sets)
Let
![]() $(X,G)$
be a dynamical system with metrizable X and let
$(X,G)$
be a dynamical system with metrizable X and let
![]() $(B_n)$
be a Følner sequence on G. Then, the following assertions for
$(B_n)$
be a Følner sequence on G. Then, the following assertions for
![]() $x\in X$
are equivalent:
$x\in X$
are equivalent:
-
(i) the point x is mean almost periodic;
-
(ii) for any
 $\delta>0$
the set of
$\delta>0$
the set of
 $t\in G$
with
$t\in G$
with  $$ \begin{align*} \operatorname{Dens}(\{s\in G : d(sx,tsx)\geq \delta\})< \varepsilon \end{align*} $$
$$ \begin{align*} \operatorname{Dens}(\{s\in G : d(sx,tsx)\geq \delta\})< \varepsilon \end{align*} $$
is relatively dense for any
 $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. We use the notation of the proof of the preceding lemma.
(i)
![]() $\Longrightarrow $
(ii): Let
$\Longrightarrow $
(ii): Let
![]() $\delta>0$
and
$\delta>0$
and
![]() $\varepsilon>0$
be arbitrary. By assertion (i), the set of
$\varepsilon>0$
be arbitrary. By assertion (i), the set of
![]() $t\in G$
with
$t\in G$
with
![]() $\overline {M}(d_{t,x})< \delta \varepsilon $
is relatively dense. Now, for any such
$\overline {M}(d_{t,x})< \delta \varepsilon $
is relatively dense. Now, for any such
![]() $t\in G$
we obtain from Proposition 3.3(a)
$t\in G$
we obtain from Proposition 3.3(a)
(ii)
![]() $\Longrightarrow $
(i): Let
$\Longrightarrow $
(i): Let
![]() $\varepsilon>0$
be given. Assume without loss of generality that
$\varepsilon>0$
be given. Assume without loss of generality that
![]() $d\leq 1$
. Set
$d\leq 1$
. Set
![]() $\delta = {\varepsilon }/{2}$
. By assertion (ii), the set of
$\delta = {\varepsilon }/{2}$
. By assertion (ii), the set of
![]() $t\in G$
with
$t\in G$
with
![]() $ \mbox {Dens}(\{s\in G : d(sx,tsx)\geq \delta \})< {\varepsilon }/{2}$
is relatively dense. Choose such a
$ \mbox {Dens}(\{s\in G : d(sx,tsx)\geq \delta \})< {\varepsilon }/{2}$
is relatively dense. Choose such a
![]() $t\in G$
. Then, Proposition 3.3(b) gives
$t\in G$
. Then, Proposition 3.3(b) gives
This finishes the proof.
We finish this section with the discussion of a further characterization of mean almost periodicity via suitable functions. To state this characterization (and similar characterizations in subsequent sections) it is useful to define for
![]() $x\in X$
and
$x\in X$
and
![]() $f\in C(X)$
the function
$f\in C(X)$
the function
Moreover, we set
Clearly,
![]() $\mathcal {A}_x$
is an algebra.
$\mathcal {A}_x$
is an algebra.
Proposition 3.6. (Completeness of
 $\mathcal {A}_x$
)
$\mathcal {A}_x$
)
The algebra
![]() $\mathcal {A}_x$
is complete with respect to
$\mathcal {A}_x$
is complete with respect to
![]() $\|\cdot \|_\infty $
.
$\|\cdot \|_\infty $
.
Proof. Consider a sequence
![]() $(f^{(n)})$
in
$(f^{(n)})$
in
![]() $C(X)$
such that
$C(X)$
such that
![]() $(f^{(n)}_x)$
is a Cauchy sequence with respect to
$(f^{(n)}_x)$
is a Cauchy sequence with respect to
![]() $\|\cdot \|_\infty $
. Then, a direct
$\|\cdot \|_\infty $
. Then, a direct
![]() $\varepsilon /3$
argument shows that the restrictions of
$\varepsilon /3$
argument shows that the restrictions of
![]() $f^{(n)}$
to the orbit closure of x converge uniformly to a continuous function on the orbit closure. Now, the desired statement follows from Tietze’s extension theorem.
$f^{(n)}$
to the orbit closure of x converge uniformly to a continuous function on the orbit closure. Now, the desired statement follows from Tietze’s extension theorem.
A bounded measurable function
![]() $f : G\longrightarrow \mathbb {C}$
is mean almost periodic with respect to
$f : G\longrightarrow \mathbb {C}$
is mean almost periodic with respect to
![]() $(B_n)$
if, for every
$(B_n)$
if, for every
![]() $\varepsilon>0$
, the set
$\varepsilon>0$
, the set
is relatively dense. The set of uniformly continuous mean almost periodic functions is an algebra and closed under complex conjugation and uniform convergence (see Appendix B).
As a consequence of the previous considerations, we can now characterize mean almost periodicity via functions.
Lemma 3.7. (Mean almost periodicity via functions)
Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence on G. For
$(B_n)$
be a Følner sequence on G. For
![]() $x\in X$
the following assertions are equivalent.
$x\in X$
the following assertions are equivalent.
-
(i) The point x is mean almost periodic.
-
(ii) Every element from
 $\mathcal {A}_x$
is mean almost periodic.
$\mathcal {A}_x$
is mean almost periodic. -
(iii) The set
 $\{f\in C(X) : f_x \mbox { is mean almost periodic}\}$
separates the points of
$\{f\in C(X) : f_x \mbox { is mean almost periodic}\}$
separates the points of
 $\overline {Gx}$
.
$\overline {Gx}$
. -
(iv) For any
 $s\in G$
the function
$s\in G$
the function
 $d^{(s)}_x$
is mean almost periodic, where
$d^{(s)}_x$
is mean almost periodic, where
 $d^{(s)} \in C(X)$
is defined via
$d^{(s)} \in C(X)$
is defined via
 $d^{(s)} (y) : =d(sx,y)$
.
$d^{(s)} (y) : =d(sx,y)$
.
Remark. As the proof shows, condition (iii) could equivalently be formulated with
![]() $\overline {Gx}$
replaced by the whole space X.
$\overline {Gx}$
replaced by the whole space X.
Proof. (iv)
![]() $\Longrightarrow $
(iii): This follows as the
$\Longrightarrow $
(iii): This follows as the
![]() $d^{(s)}$
,
$d^{(s)}$
,
![]() $s\in G$
, clearly separate the points of
$s\in G$
, clearly separate the points of
![]() $\overline {Gx}$
.
$\overline {Gx}$
.
(iii)
![]() $\Longrightarrow $
(ii): Invoking the corresponding properties of mean almost periodic functions, we can easily see that
$\Longrightarrow $
(ii): Invoking the corresponding properties of mean almost periodic functions, we can easily see that
![]() $\{f \in C(X) : f_x \mbox { is mean almost periodic}\}$
is an algebra, which is closed under complex conjugation and uniform convergence. This algebra clearly contains the constant functions. Moreover, by assumption (iii), it separates the points of
$\{f \in C(X) : f_x \mbox { is mean almost periodic}\}$
is an algebra, which is closed under complex conjugation and uniform convergence. This algebra clearly contains the constant functions. Moreover, by assumption (iii), it separates the points of
![]() $\overline {Gx}$
. Furthermore this algebra contains every function
$\overline {Gx}$
. Furthermore this algebra contains every function
![]() $f\in C(X)$
, which vanishes on
$f\in C(X)$
, which vanishes on
![]() $\overline {Gx}$
(as
$\overline {Gx}$
(as
![]() $f_x = 0$
for any such functions). Thus, this algebra even separates the points of X. Now, assumption (ii) follows from Stone–Weierstraß’ theorem.
$f_x = 0$
for any such functions). Thus, this algebra even separates the points of X. Now, assumption (ii) follows from Stone–Weierstraß’ theorem.
(ii)
![]() $\Longrightarrow $
(i): Choose a countable set
$\Longrightarrow $
(i): Choose a countable set
![]() $\mathcal {C} \subset C(X)$
such that any
$\mathcal {C} \subset C(X)$
such that any
![]() $f\in \mathcal {C}$
satisfies
$f\in \mathcal {C}$
satisfies
![]() $\|f\|_\infty \leq 1$
and such that the elements of
$\|f\|_\infty \leq 1$
and such that the elements of
![]() $\mathcal {C}$
separate the points of X. Let
$\mathcal {C}$
separate the points of X. Let
![]() $c_f>0$
,
$c_f>0$
,
![]() $f\in \mathcal {C}$
, with
$f\in \mathcal {C}$
, with
![]() $\sum _{f\in \mathcal {C}} c_f <\infty $
be given. Then,
$\sum _{f\in \mathcal {C}} c_f <\infty $
be given. Then,
 $$ \begin{align*}e (z,y) := \sum_{f\in \mathcal{C}} c_f\, |f(x) - f(y)|\end{align*} $$
$$ \begin{align*}e (z,y) := \sum_{f\in \mathcal{C}} c_f\, |f(x) - f(y)|\end{align*} $$
is a metric on X, which generates the topology. Moreover, by assumption (ii), the function
![]() $f_x$
is mean almost periodic for any
$f_x$
is mean almost periodic for any
![]() $f\in C(X)$
and, hence, any
$f\in C(X)$
and, hence, any
![]() $f\in \mathcal {C}$
. This easily gives that the set of
$f\in \mathcal {C}$
. This easily gives that the set of
![]() $t\in G$
with
$t\in G$
with
![]() $\overline {M}(s\mapsto e(sx,(t+s)x)) <\varepsilon $
is relatively dense (compare with Proposition B.4). Thus, x is mean almost periodic with respect to the metric e. As mean almost periodicity does not depend on the metric, we conclude the proof of assumption (i).
$\overline {M}(s\mapsto e(sx,(t+s)x)) <\varepsilon $
is relatively dense (compare with Proposition B.4). Thus, x is mean almost periodic with respect to the metric e. As mean almost periodicity does not depend on the metric, we conclude the proof of assumption (i).
(i)
![]() $\Longrightarrow $
(iv): Let
$\Longrightarrow $
(iv): Let
![]() $z\in X$
be arbitrary and define
$z\in X$
be arbitrary and define
![]() $d^{(z)} \in C(X)$
by
$d^{(z)} \in C(X)$
by
![]() $d^{(z)} (y):= d(z,y)$
. The triangle inequality for d gives
$d^{(z)} (y):= d(z,y)$
. The triangle inequality for d gives
 $$ \begin{align*}\overline{M}( |d^{(z_x)} (\cdot - t) - d^{(z)}_x|)&= \overline{M}( s\mapsto |d(z,(s-t)x) - d(z,sx)|)\\ &\leq \overline{M}(s\mapsto d(sx, (s-t)x)) = D(x,-tx)\end{align*} $$
$$ \begin{align*}\overline{M}( |d^{(z_x)} (\cdot - t) - d^{(z)}_x|)&= \overline{M}( s\mapsto |d(z,(s-t)x) - d(z,sx)|)\\ &\leq \overline{M}(s\mapsto d(sx, (s-t)x)) = D(x,-tx)\end{align*} $$
for any
![]() $t\in G$
and
$t\in G$
and
![]() $z\in X$
. Now, mean almost periodicity of
$z\in X$
. Now, mean almost periodicity of
![]() $d^z_x (\cdot )$
follows (for any
$d^z_x (\cdot )$
follows (for any
![]() $z\in X$
) from assumption (i).
$z\in X$
) from assumption (i).
We now come to the main result of this section, which provides a characterization of pure point spectrum via mean almost periodic points.
Theorem 3.8. Let
![]() $(X,G,m)$
be a dynamical system and let
$(X,G,m)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence on G. Assume that there exists a generic point for
$(B_n)$
be a Følner sequence on G. Assume that there exists a generic point for
![]() $(X,G,m)$
. Then, the following assertions are equivalent.
$(X,G,m)$
. Then, the following assertions are equivalent.
-
(i) The dynamical system
 $(X,G,m)$
has pure point spectrum.
$(X,G,m)$
has pure point spectrum. -
(ii) Every generic point of X is mean almost periodic.
-
(iii) One generic point of X is mean almost periodic.
If
![]() $(X,G,m)$
is ergodic and the Birkhoff theorem holds along
$(X,G,m)$
is ergodic and the Birkhoff theorem holds along
![]() $(B_n)$
, these statements are also equivalent to the following statement.
$(B_n)$
, these statements are also equivalent to the following statement.
-
(iv) Almost every
 $x\in X$
is mean almost periodic.
$x\in X$
is mean almost periodic.
Remark
-
(a) In the particular case of point processes in
 $\mathbb {R}^d$
, this result has been proven in [Reference Gouéré21, Theorem 4.4].
$\mathbb {R}^d$
, this result has been proven in [Reference Gouéré21, Theorem 4.4]. -
(b) A related result for subshifts over a finite alphabet can be found in [Reference Vershik40, Lemma 5]. There, pure point spectrum (i) is characterized via a variant of statement (iv) given by a mean almost periodicity condition on points defined via a metric (close in spirit to what is discussed in Lemma 3.5).
It is worth noting here that in [Reference Vershik40] the author works over a finite alphabet and uses a version of the mean defined with
 $\liminf $
. Under the settings of [Reference Vershik40], assuming ergodicity, one can show that the limit exists almost surely, and hence the choice of
$\liminf $
. Under the settings of [Reference Vershik40], assuming ergodicity, one can show that the limit exists almost surely, and hence the choice of
 $\liminf $
or
$\liminf $
or
 $\limsup $
does not matter. In particular, for ergodic systems, one can deduce [Reference Vershik40, Lemma 5] from our result. We prefer to work with
$\limsup $
does not matter. In particular, for ergodic systems, one can deduce [Reference Vershik40, Lemma 5] from our result. We prefer to work with
 $\limsup $
because it defines a pseudo-metric, whereas
$\limsup $
because it defines a pseudo-metric, whereas
 $\liminf $
only gives rise to a partial semi-metric.
$\liminf $
only gives rise to a partial semi-metric. -
(c) The equivalence between mean almost periodicity of an individual element and pure point diffraction has been proven for constant length substitutions in [Reference Queffélec36, Lemma VI.25], for Meyer sets in [Reference Baake and Moody6, Reference Gouéré21] and in general in [Reference Lenz, Spindeler and Strungaru31].
Proof. In the ergodic case almost every point is generic. Hence, (ii)
![]() $\Longrightarrow $
(iv) and (iv)
$\Longrightarrow $
(iv) and (iv)
![]() $\Longrightarrow $
(iii) follow. Thus, we now turn to showing equivalence between assertions (i), (ii) and (iii) in the general case. We clearly have (ii)
$\Longrightarrow $
(iii) follow. Thus, we now turn to showing equivalence between assertions (i), (ii) and (iii) in the general case. We clearly have (ii)
![]() $\Longrightarrow $
(iii). To show (i)
$\Longrightarrow $
(iii). To show (i)
![]() $\Longrightarrow $
(ii) and (iii)
$\Longrightarrow $
(ii) and (iii)
![]() $\Longrightarrow $
(i) we define
$\Longrightarrow $
(i) we define
The main result of [Reference Lenz29] says that assertion (i) is equivalent to
![]() $\underline {d}$
being Bohr almost periodic. Thus, it remains to show that:
$\underline {d}$
being Bohr almost periodic. Thus, it remains to show that:
-
• Bohr almost periodicity of
 $\underline {d}$
implies (ii);
$\underline {d}$
implies (ii); -
• (iii) implies Bohr almost periodicity of
 $\underline {d}$
.
$\underline {d}$
.
Now, for
![]() $t\in G$
we can consider
$t\in G$
we can consider
![]() $f_t : X\longrightarrow [0,\infty ),\ f_t (x) = d(x,tx)$
. Then,
$f_t : X\longrightarrow [0,\infty ),\ f_t (x) = d(x,tx)$
. Then,
![]() $f_t$
is clearly continuous. Thus, whenever
$f_t$
is clearly continuous. Thus, whenever
![]() $y\in X$
is generic, we find
$y\in X$
is generic, we find
for every
![]() $t\in G$
. Moreover, the triangle inequality gives that
$t\in G$
. Moreover, the triangle inequality gives that
![]() $\underline {d}$
is Bohr almost periodic if and only if the set
$\underline {d}$
is Bohr almost periodic if and only if the set
is relatively dense in G for all
![]() $\varepsilon>0$
. Putting this together we easily obtain that
$\varepsilon>0$
. Putting this together we easily obtain that
![]() $\underline {d}$
is Bohr almost periodic if and only if one (every) generic
$\underline {d}$
is Bohr almost periodic if and only if one (every) generic
![]() $y\in X$
is mean almost periodic.
$y\in X$
is mean almost periodic.
We emphasize that the first part of the preceding theorem does not need an ergodicity assumption and illustrate this using the following example.
Example: pure point spectrum in non ergodic case. Consider
![]() $\{0,1\}$
with discrete topology and
$\{0,1\}$
with discrete topology and
![]() $X = \{0,1\}^{\mathbb {Z}}$
with product topology. Equip X with the shift action of
$X = \{0,1\}^{\mathbb {Z}}$
with product topology. Equip X with the shift action of
![]() $\mathbb {Z}$
given by
$\mathbb {Z}$
given by
![]() $\alpha _n(x) = x(\cdot - n)$
for
$\alpha _n(x) = x(\cdot - n)$
for
![]() $n\in \mathbb {Z}$
. Let
$n\in \mathbb {Z}$
. Let
![]() $\underline {1}$
and
$\underline {1}$
and
![]() $\underline {0}$
be the elements of X which are constant equal to
$\underline {0}$
be the elements of X which are constant equal to
![]() $1$
and
$1$
and
![]() $0$
, respectively. Then, clearly each of these elements is invariant under the shift action and so are then the sets
$0$
, respectively. Then, clearly each of these elements is invariant under the shift action and so are then the sets
![]() $\{\underline {0}\}$
and
$\{\underline {0}\}$
and
![]() $\{\underline {1}\}$
. Thus,
$\{\underline {1}\}$
. Thus,
is an invariant probability measure (where
![]() $\delta _p$
denotes the unit point mass at p). Obviously, m is not ergodic. The space
$\delta _p$
denotes the unit point mass at p). Obviously, m is not ergodic. The space
![]() $L^2(X,m)$
is two-dimensional and
$L^2(X,m)$
is two-dimensional and
![]() $\sqrt {2} \cdot 1_{\{\underline {0}\}}, \sqrt {2} \cdot 1_{\{\underline {1}\}}$
is an orthogonal basis consisting of eigenfunctions (to the eigenvalue
$\sqrt {2} \cdot 1_{\{\underline {0}\}}, \sqrt {2} \cdot 1_{\{\underline {1}\}}$
is an orthogonal basis consisting of eigenfunctions (to the eigenvalue
![]() $1$
). In particular,
$1$
). In particular,
![]() $(X,\mathbb {Z},m)$
has pure point spectrum. Now, consider the point
$(X,\mathbb {Z},m)$
has pure point spectrum. Now, consider the point
![]() $x\in X$
with
$x\in X$
with
![]() $x(-k)$
arbitrary for
$x(-k)$
arbitrary for
![]() $k\geq 0$
and
$k\geq 0$
and
![]() $x(k) = 1 $
if
$x(k) = 1 $
if
![]() $k\in \{2^n,\ldots , 2^n +2^{n-1}-1\}$
for some
$k\in \{2^n,\ldots , 2^n +2^{n-1}-1\}$
for some
![]() $n\in \mathbb {N}$
and
$n\in \mathbb {N}$
and
![]() $x(k) =0$
otherwise. Then, it is not hard to see that x is generic for m with respect to the Følner sequence
$x(k) =0$
otherwise. Then, it is not hard to see that x is generic for m with respect to the Følner sequence
![]() $B_n =\{1,\ldots , 2^n\}$
. Thus, the theorem gives that x is mean almost periodic. In this example neither
$B_n =\{1,\ldots , 2^n\}$
. Thus, the theorem gives that x is mean almost periodic. In this example neither
![]() $\underline {0}$
nor
$\underline {0}$
nor
![]() $\underline {1}$
are generic. Hence, m does not give mass to generic points and the set of generic points has measure zero. Note that the construction of x could easily be modified to yield a transitive generic point (by including suitable finite words of slowly increasing length between the blocks of ones and zeros in x).
$\underline {1}$
are generic. Hence, m does not give mass to generic points and the set of generic points has measure zero. Note that the construction of x could easily be modified to yield a transitive generic point (by including suitable finite words of slowly increasing length between the blocks of ones and zeros in x).
Combining the previous result, Theorem 3.8, with the characterization of mean almost periodicity via functions in Lemma 3.7, we obtain the following.
Corollary 3.9. Let
![]() $(X,G,m)$
be an ergodic dynamical system with metrizable X and assume that Birkhoff’s ergodic theorem holds along
$(X,G,m)$
be an ergodic dynamical system with metrizable X and assume that Birkhoff’s ergodic theorem holds along
![]() $(B_n)$
. Then, the following assertions are equivalent.
$(B_n)$
. Then, the following assertions are equivalent.
-
(i) The dynamical system
 $(X,G,m)$
has pure point spectrum.
$(X,G,m)$
has pure point spectrum. -
(ii) For almost every
 $x\in X$
the set
$x\in X$
the set
 $\{f \in C(X) : f_x \mbox { is mean almost periodic}\}$
separates the points of X.
$\{f \in C(X) : f_x \mbox { is mean almost periodic}\}$
separates the points of X.
Remark. A variant of this statement (with assertion (ii) replaced by the stronger condition that
![]() $\mathcal {A}_x$
consists only of mean almost periodic functions) is shown in [Reference Lenz28] based on an earlier version of [Reference Lenz, Spindeler and Strungaru31]. Our proof is different. Note also that for ergodic systems over
$\mathcal {A}_x$
consists only of mean almost periodic functions) is shown in [Reference Lenz28] based on an earlier version of [Reference Lenz, Spindeler and Strungaru31]. Our proof is different. Note also that for ergodic systems over
![]() $G = \mathbb {Z}$
, it is known that pure point spectrum is equivalent to
$G = \mathbb {Z}$
, it is known that pure point spectrum is equivalent to
![]() $\mathbb {Z}\ni n\mapsto f(nx)$
belonging to the Besicovitch class for almost every
$\mathbb {Z}\ni n\mapsto f(nx)$
belonging to the Besicovitch class for almost every
![]() $x\in X$
whenever f is a bounded measurable function on X, see Theorem 3.22 in [Reference Bellow and Losert7]. The condition of Besicovitch class is stronger than mean almost periodicity (see also the next section).
$x\in X$
whenever f is a bounded measurable function on X, see Theorem 3.22 in [Reference Bellow and Losert7]. The condition of Besicovitch class is stronger than mean almost periodicity (see also the next section).
If the system
![]() $(X,G,m)$
is uniquely ergodic, then every
$(X,G,m)$
is uniquely ergodic, then every
![]() $x\in X$
is generic irrespective of the underlying Følner sequence (Oxtoby’s theorem). Thus, from the previous theorem we obtain immediately the following corollary.
$x\in X$
is generic irrespective of the underlying Følner sequence (Oxtoby’s theorem). Thus, from the previous theorem we obtain immediately the following corollary.
Corollary 3.10. Let
![]() $(X,G,m)$
be a dynamical system and let
$(X,G,m)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence on G. Assume that
$(B_n)$
be a Følner sequence on G. Assume that
![]() $(X,G,m)$
is uniquely ergodic. Then, the following assertions are equivalent.
$(X,G,m)$
is uniquely ergodic. Then, the following assertions are equivalent.
-
(i) The dynamical system
 $(X,G,m)$
has pure point spectrum.
$(X,G,m)$
has pure point spectrum. -
(ii) Every
 $x\in X$
is mean almost periodic.
$x\in X$
is mean almost periodic. -
(iii) One
 $x\in X$
is mean almost periodic.
$x\in X$
is mean almost periodic.
Remark. The concept of mean almost periodicity depends on the chosen Følner sequence. To see this, consider
![]() $X:=\{0,1\}^{\mathbb {Z}}$
with product topology and the shift action of
$X:=\{0,1\}^{\mathbb {Z}}$
with product topology and the shift action of
![]() $\mathbb {Z}$
and the Bernoulli measure m (product measure of the measures giving equal weights
$\mathbb {Z}$
and the Bernoulli measure m (product measure of the measures giving equal weights
![]() $1/2$
to
$1/2$
to
![]() $\{0\}$
and
$\{0\}$
and
![]() $\{1\}$
). This system is ergodic and m almost every
$\{1\}$
). This system is ergodic and m almost every
![]() $x\in X$
contains arbitrary long stretches of zeros. For each of those x we can then choose a Følner sequence
$x\in X$
contains arbitrary long stretches of zeros. For each of those x we can then choose a Følner sequence
![]() $(B_n)$
with
$(B_n)$
with
![]() $\overline {M}(s\mapsto d(sx,(t+s)x) = 0$
for all
$\overline {M}(s\mapsto d(sx,(t+s)x) = 0$
for all
![]() $t\in \mathbb {Z}$
(by each
$t\in \mathbb {Z}$
(by each
![]() $B_n$
being chosen ‘within’ a long stretch of zeros with distance to the boundary of these stretches increasing in n). Hence, each of these x is mean almost periodic. On the other hand, as the system does not have pure point spectrum, we obtain from Theorem 3.8 that not every of these x will be almost periodic with respect to the standard Følner sequence
$B_n$
being chosen ‘within’ a long stretch of zeros with distance to the boundary of these stretches increasing in n). Hence, each of these x is mean almost periodic. On the other hand, as the system does not have pure point spectrum, we obtain from Theorem 3.8 that not every of these x will be almost periodic with respect to the standard Følner sequence
![]() $B_n = \{0,\ldots ,n\}$
along which Birkhoff’s ergodic theorem holds.
$B_n = \{0,\ldots ,n\}$
along which Birkhoff’s ergodic theorem holds.
4 Besicovitch almost periodic points and eigenfunctions
In this section, we discuss a strengthened version of mean almost periodicity, namely Besicovitch almost periodicity. We show that pure point spectrum can also be characterized via this strengthened version. In fact, our results can be understood as saying that in a dynamical system with pure point spectrum both eigenfunctions and eigenvalues can be read of from any of its (generic) Besicovitch almost periodic points.
We consider a
![]() $\sigma $
-compact, locally compact abelian group together with a Følner sequence
$\sigma $
-compact, locally compact abelian group together with a Følner sequence
![]() $(B_n)$
. As usual, the set of all continuous group homomorphisms
$(B_n)$
. As usual, the set of all continuous group homomorphisms
![]() $\xi : G\longrightarrow \mathbb {T}$
is denoted as
$\xi : G\longrightarrow \mathbb {T}$
is denoted as
![]() $\widehat {G}$
and called the dual group of G. We say that a bounded function
$\widehat {G}$
and called the dual group of G. We say that a bounded function
![]() $f : G\longrightarrow \mathbb {C}$
is Besicovitch almost periodic if for any
$f : G\longrightarrow \mathbb {C}$
is Besicovitch almost periodic if for any
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
and
$\xi _1,\ldots , \xi _k\in \widehat {G}$
and
![]() $c_1,\ldots ,c_k\in \mathbb {C}$
with
$c_1,\ldots ,c_k\in \mathbb {C}$
with
 $$ \begin{align*}\overline{M} \bigg(\bigg|f - \sum_{j=1}^k c_j \xi_j\bigg|\bigg)< \varepsilon.\end{align*} $$
$$ \begin{align*}\overline{M} \bigg(\bigg|f - \sum_{j=1}^k c_j \xi_j\bigg|\bigg)< \varepsilon.\end{align*} $$
A discussion of basic properties of uniformly continuous Besicovitch almost periodic functions is given in Appendix C. This shows, in particular, that any uniformly continuous Besicovitch almost periodic function is also mean almost periodic and admits an average (see also the following). The discussion also shows that the set of these functions forms an algebra and is closed under uniform convergence.
Definition 4.1. (Besicovitch almost periodic points)
Let
![]() $(X,G)$
be a metrizable dynamical system and let
$(X,G)$
be a metrizable dynamical system and let
![]() $(B_n)$
be a Følner sequence. Then, a point
$(B_n)$
be a Følner sequence. Then, a point
![]() $x\in X$
is called Besicovitch almost periodic with respect to
$x\in X$
is called Besicovitch almost periodic with respect to
![]() $(B_n)$
if
$(B_n)$
if
![]() $\mathcal {A}_x$
consists only of Besicovitch almost periodic functions.
$\mathcal {A}_x$
consists only of Besicovitch almost periodic functions.
As in the definition of mean almost periodicity, Besicovitch almost periodicity also depends on the chosen Følner sequence. In our subsequent discussion, however, we often refrain from explicitly referring to the Følner sequence
![]() $(B_n)$
if it is clear from the context which sequence is involved.
$(B_n)$
if it is clear from the context which sequence is involved.
Remark
-
(a) To set this definition in perspective, we refer to Lemma 3.7. This lemma shows that a point is mean almost periodic if and only if
 $\mathcal {A}_x$
consists of mean almost periodic functions only.
$\mathcal {A}_x$
consists of mean almost periodic functions only. -
(b) Note also that the statements of Lemma 3.7 remain true (with essentially the same proof) after ‘mean almost periodic’ is replaced with ‘Besicovitch almost periodic’.
-
(c) As Besicovitch almost periodic functions are mean almost periodic, any Besicovitch almost periodic point is mean almost periodic. The converse is not true. To see this consider
 $X:=\{0,1\}^{\mathbb {Z}}$
with product topology and the shift action of
$X:=\{0,1\}^{\mathbb {Z}}$
with product topology and the shift action of
 $\mathbb {Z}$
. Set
$\mathbb {Z}$
. Set
 $B_n :=\{0,\ldots , n\}$
for n even and
$B_n :=\{0,\ldots , n\}$
for n even and
 $B_n = \{-n,\ldots , -1\}$
for n odd. Consider now
$B_n = \{-n,\ldots , -1\}$
for n odd. Consider now
 $y\in X$
with
$y\in X$
with
 $y(k) = 1 $
for
$y(k) = 1 $
for
 $k\geq 0$
and
$k\geq 0$
and
 $y(k) = 0$
otherwise. Then, it is not hard to see that
$y(k) = 0$
otherwise. Then, it is not hard to see that
 $D(y,ny) = 0$
for all
$D(y,ny) = 0$
for all
 $n\in \mathbb {Z}$
. Hence, y is mean almost periodic. On the other hand, consider
$n\in \mathbb {Z}$
. Hence, y is mean almost periodic. On the other hand, consider
 $f: X\longrightarrow \{0,1\}$
with
$f: X\longrightarrow \{0,1\}$
with
 $f(x) = x(0)$
. Clearly f is continuous. Moreover, does not converge (as
$f(x) = x(0)$
. Clearly f is continuous. Moreover, does not converge (as $$ \begin{align*}a_n :=\frac{1}{|B_n|} \sum_{k\in B_n} f(k y)\end{align*} $$
$$ \begin{align*}a_n :=\frac{1}{|B_n|} \sum_{k\in B_n} f(k y)\end{align*} $$
 $a_{2n} =1$
and
$a_{2n} =1$
and
 $a_{2n+1} =0$
for all
$a_{2n+1} =0$
for all
 $n\in \mathbb {N}$
). By the discussion in Appendix C (see also Proposition 4.2), this shows that
$n\in \mathbb {N}$
). By the discussion in Appendix C (see also Proposition 4.2), this shows that
 $f_y$
is not Besicovitch almost periodic. Hence, y is not Besicovitch almost periodic.
$f_y$
is not Besicovitch almost periodic. Hence, y is not Besicovitch almost periodic.
We now give a characterization of Besicovitch almost periodic points via existence of means. To state it, we first introduce some notation. For a bounded measurable function
![]() $h: G\longrightarrow \mathbb {C}$
, we define the mean or average of h with respect to
$h: G\longrightarrow \mathbb {C}$
, we define the mean or average of h with respect to
![]() $(B_n)$
by
$(B_n)$
by
 $$ \begin{align*} \mathrm{A}(h):= \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} h(t)\,d t \end{align*} $$
$$ \begin{align*} \mathrm{A}(h):= \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} h(t)\,d t \end{align*} $$
whenever the limit exists.
Proposition 4.2. (Averaging along orbits)
Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence. Then, the following assertions are equivalent for
$(B_n)$
be a Følner sequence. Then, the following assertions are equivalent for
![]() $x\in X$
.
$x\in X$
.
-
(i) The point x is Besicovitch almost periodic.
-
(ii) For any
 $f\in C(X)$
there exists a countable set
$f\in C(X)$
there exists a countable set
 $F_f\subset \widehat {G}$
such that the limits exist for all
$F_f\subset \widehat {G}$
such that the limits exist for all $$ \begin{align*}\hspace{-15pt} \mathrm{A}( |f_x|^2) = \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} |f(tx)|^2 \,d t \quad \mbox{and} \quad \mathrm{A}(f_x \overline{\xi}) =\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(tx)\, \overline{\xi(t)} \,d t \end{align*} $$
$$ \begin{align*}\hspace{-15pt} \mathrm{A}( |f_x|^2) = \lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} |f(tx)|^2 \,d t \quad \mbox{and} \quad \mathrm{A}(f_x \overline{\xi}) =\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(tx)\, \overline{\xi(t)} \,d t \end{align*} $$
 $\xi \in F_f$
and holds.
$\xi \in F_f$
and holds. $$ \begin{align*} \mathrm{A}(|f_x|^2) =\sum_{\xi \in F_f} |\mathrm{A}(f_x \overline{\xi})|^2 \end{align*} $$
$$ \begin{align*} \mathrm{A}(|f_x|^2) =\sum_{\xi \in F_f} |\mathrm{A}(f_x \overline{\xi})|^2 \end{align*} $$
Moreover, in case that assertions (i) and (ii) hold,
![]() $A(f\overline {\xi })$
exists and equals zero for
$A(f\overline {\xi })$
exists and equals zero for
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\xi \in \widehat {G}\setminus F_f$
.
$\xi \in \widehat {G}\setminus F_f$
.
Proof. This is a direct consequence of the definition of Besicovitch almost periodicity of a point and Proposition C.4 in Appendix C.
Definition 4.3. (Frequency)
Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $x\in X$
be a Besicovitch almost periodic point. Then, every
$x\in X$
be a Besicovitch almost periodic point. Then, every
![]() $\xi \in \widehat {G}$
with
$\xi \in \widehat {G}$
with
![]() $\mathrm {A}( f_x\overline {\xi }) \neq 0$
for some
$\mathrm {A}( f_x\overline {\xi }) \neq 0$
for some
![]() $f\in C(X)$
is called a frequency of x. The set of all frequencies of x is denoted by
$f\in C(X)$
is called a frequency of x. The set of all frequencies of x is denoted by
![]() $\mathrm {Freq}(x)$
.
$\mathrm {Freq}(x)$
.
Here is the first main result of this section. It shows that any Besicovitch almost periodic point completely determines a dynamical system with pure point spectrum.
Theorem 4.4. Let
![]() $(X,G)$
be a dynamical system, let
$(X,G)$
be a dynamical system, let
![]() $(B_n)$
be a Følner sequence and let
$(B_n)$
be a Følner sequence and let
![]() $p\in X$
be a Besicovitch almost periodic point. Then, there exists a (unique) ergodic probability measure m on X such that p is generic with respect to m. The dynamical system
$p\in X$
be a Besicovitch almost periodic point. Then, there exists a (unique) ergodic probability measure m on X such that p is generic with respect to m. The dynamical system
![]() $(X,G,m)$
has pure point spectrum and
$(X,G,m)$
has pure point spectrum and
![]() $\mathrm {Eig}(X,G,m) =\mathrm {Freq}(p)$
holds. To each eigenvalue
$\mathrm {Eig}(X,G,m) =\mathrm {Freq}(p)$
holds. To each eigenvalue
![]() $\xi \in \mathrm {Eig}(X,G,m)$
there exists a (unique) eigenfunction
$\xi \in \mathrm {Eig}(X,G,m)$
there exists a (unique) eigenfunction
![]() $e_\xi \in L^2 (X,m)$
with
$e_\xi \in L^2 (X,m)$
with
for all
![]() $f\in C(X)$
.
$f\in C(X)$
.
Proof. Obviously, the map
is linear and positive (that is,
![]() $\mathrm {A}(f_p)\geq 0$
for
$\mathrm {A}(f_p)\geq 0$
for
![]() $f\geq 0$
). Hence, there exists a unique measure m on X with
$f\geq 0$
). Hence, there exists a unique measure m on X with
![]() $\Phi (f) = \int _X f\,d m$
. Clearly,
$\Phi (f) = \int _X f\,d m$
. Clearly,
![]() $m(X) = \int _X 1\,d m = \mathrm {A}(1) = 1$
. By the Følner property of
$m(X) = \int _X 1\,d m = \mathrm {A}(1) = 1$
. By the Følner property of
![]() $(B_n)$
, the mean
$(B_n)$
, the mean
![]() $\mathrm {A}$
is invariant and, thus, so is
$\mathrm {A}$
is invariant and, thus, so is
![]() $\Phi $
. This easily gives that m is invariant. Thus, m is an invariant probability measure.
$\Phi $
. This easily gives that m is invariant. Thus, m is an invariant probability measure.
We now turn to the construction of the eigenfunctions. For
![]() $\xi \in \widehat {G}$
consider the map
$\xi \in \widehat {G}$
consider the map
This map is obviously linear and defined on a dense subspace of
![]() $L^2 (X,m)$
. By the Cauchy–Schwarz inequality,
$L^2 (X,m)$
. By the Cauchy–Schwarz inequality,
![]() $\mathrm {A}(1) =1$
and the construction of m we find
$\mathrm {A}(1) =1$
and the construction of m we find
Hence,
![]() $\Phi _\xi $
can be extended to a linear continuous map, again denoted by
$\Phi _\xi $
can be extended to a linear continuous map, again denoted by
![]() $\Phi _\xi $
, on the whole
$\Phi _\xi $
, on the whole
![]() $L^2 (X,m)$
. By Riesz’s lemma, there exists an
$L^2 (X,m)$
. By Riesz’s lemma, there exists an
![]() $e_\xi \in L^2 (X,m)$
with
$e_\xi \in L^2 (X,m)$
with
![]() $\|e_\xi \|\leq 1$
and
$\|e_\xi \|\leq 1$
and
for all
![]() $f\in C(X)$
. Define
$f\in C(X)$
. Define
By construction,
![]() $\xi \in \widehat {G}$
belongs to E if and only if there exists an
$\xi \in \widehat {G}$
belongs to E if and only if there exists an
![]() $f\in C(X)$
with
$f\in C(X)$
with
![]() $\mathrm {A}(f_p \overline {\xi }) \neq 0$
. Hence,
$\mathrm {A}(f_p \overline {\xi }) \neq 0$
. Hence,
![]() $E= \mathrm {Freq}(p)$
holds. In particular, we have
$E= \mathrm {Freq}(p)$
holds. In particular, we have
![]() $\mathrm {A}(f_p \overline {\varrho })=0$
for all
$\mathrm {A}(f_p \overline {\varrho })=0$
for all
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\varrho \in \widehat {G}\setminus E$
. A short computation shows for
$\varrho \in \widehat {G}\setminus E$
. A short computation shows for
![]() $t\in G$
,
$t\in G$
,
 $$ \begin{align*} \xi(-t) \int_X f\,\overline{ e_\xi}\,d m &= \xi(-t) \mathrm{A}(f_p \overline{\xi})\\ &= \mathrm{A}(f_p \overline{\xi(t +\cdot )})\\ (\mathrm{A} \mbox{ invariant})&= \mathrm{A}(f_p(-t\cdot) \overline{\xi})\\ (\mbox{construction of } m) &= \int_X f(-t\cdot)\, \overline{e_\xi}\,d m\\ (m \mbox{ invariant})&= \int_X f\, \overline{e_\xi(t\cdot)}\,d m \end{align*} $$
$$ \begin{align*} \xi(-t) \int_X f\,\overline{ e_\xi}\,d m &= \xi(-t) \mathrm{A}(f_p \overline{\xi})\\ &= \mathrm{A}(f_p \overline{\xi(t +\cdot )})\\ (\mathrm{A} \mbox{ invariant})&= \mathrm{A}(f_p(-t\cdot) \overline{\xi})\\ (\mbox{construction of } m) &= \int_X f(-t\cdot)\, \overline{e_\xi}\,d m\\ (m \mbox{ invariant})&= \int_X f\, \overline{e_\xi(t\cdot)}\,d m \end{align*} $$
for all
![]() $f\in C(X)$
. As these f are dense in
$f\in C(X)$
. As these f are dense in
![]() $L^2(X,m)$
this gives
$L^2(X,m)$
this gives
for all
![]() $t\in G$
. This shows that
$t\in G$
. This shows that
![]() $e_\xi $
is an eigenfunction (to
$e_\xi $
is an eigenfunction (to
![]() $\xi $
) for each
$\xi $
) for each
![]() $\xi \in E$
. Clearly, eigenfunctions to different eigenvalues are orthogonal.
$\xi \in E$
. Clearly, eigenfunctions to different eigenvalues are orthogonal.
Next, we show that the
![]() $e_\xi $
,
$e_\xi $
,
![]() $\xi \in E$
, are normalized and form a basis. This gives that
$\xi \in E$
, are normalized and form a basis. This gives that
![]() $E=\mathrm {Eig}(X,G,m)$
and together with the already shown
$E=\mathrm {Eig}(X,G,m)$
and together with the already shown
![]() $E = \mathrm {Freq}(p)$
, this will then also imply
$E = \mathrm {Freq}(p)$
, this will then also imply
![]() $\mathrm {Eig}(X,G,m) = \mathrm {Freq}(p)$
.
$\mathrm {Eig}(X,G,m) = \mathrm {Freq}(p)$
.
By Parseval’s inequality, the definition of m and Proposition 4.2, we have the following:
 $$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 &\leq \int_X |f|^2\,d m\\ &= \mathrm{A}(|f_p|^2)\\ (\textrm{Proposition}\, 4.2)&= \sum_{\xi\in \widehat{G}} |\mathrm{A}(f_p\overline{\xi})|^2\\ (\mbox{construction of } E) &= \sum_{\xi\in E} |\mathrm{A}(f_p\overline{\xi})|^2\\ (\mbox{construction of } e_\xi) &= \sum_{\xi\in E} \bigg|\int_X f\,\overline{e_\xi}\,d m\bigg|^2. \end{align*} $$
$$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 &\leq \int_X |f|^2\,d m\\ &= \mathrm{A}(|f_p|^2)\\ (\textrm{Proposition}\, 4.2)&= \sum_{\xi\in \widehat{G}} |\mathrm{A}(f_p\overline{\xi})|^2\\ (\mbox{construction of } E) &= \sum_{\xi\in E} |\mathrm{A}(f_p\overline{\xi})|^2\\ (\mbox{construction of } e_\xi) &= \sum_{\xi\in E} \bigg|\int_X f\,\overline{e_\xi}\,d m\bigg|^2. \end{align*} $$
This shows
 $$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 = \int_X |f|^2\,d m \end{align*} $$
$$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 = \int_X |f|^2\,d m \end{align*} $$
for all
![]() $f\in C(X)$
. This is only possible if
$f\in C(X)$
. This is only possible if
![]() $\|e_\xi \| =1$
for all
$\|e_\xi \| =1$
for all
![]() $\xi \in E$
and
$\xi \in E$
and
![]() $(e_\xi )$
form an orthonormal basis of
$(e_\xi )$
form an orthonormal basis of
![]() $L^2 (X,m)$
.
$L^2 (X,m)$
.
It remains to show ergodicity: for each eigenvalue
![]() $\xi \in E$
we have constructed an eigenfunction
$\xi \in E$
we have constructed an eigenfunction
![]() $e_\xi $
and we have shown that these form a complete set (that is,
$e_\xi $
and we have shown that these form a complete set (that is,
![]() $e_\xi $
,
$e_\xi $
,
![]() $ \xi \in E$
, is an orthonormal basis). Hence (as each of these eigenfunctions belong to different eigenspaces), each eigenspace is one dimensional. In particular. the eigenspace to the eigenvalue
$ \xi \in E$
, is an orthonormal basis). Hence (as each of these eigenfunctions belong to different eigenspaces), each eigenspace is one dimensional. In particular. the eigenspace to the eigenvalue
![]() $1$
is one dimensional and the system is ergodic.
$1$
is one dimensional and the system is ergodic.
Remark. Note that the proof relies (and only relies) on the characterizing properties of Besicovitch almost periodic points given in Proposition 4.2.
The previous theorem shows that any Besicovitch almost periodic point is generic with respect to a (uniquely determined) measure. It may well be that different Besicovitch almost periodic points are generic with respect to different measures. Consider, for example, the full shift
![]() $X=\{0,1\}^{\mathbb {Z}}$
with
$X=\{0,1\}^{\mathbb {Z}}$
with
![]() $T x (n) = x(n+1)$
. Then, any periodic element of X is Besicovitch almost periodic. Clearly, elements with different periods will not be generic with respect to the same measure. This motivates the following definition.
$T x (n) = x(n+1)$
. Then, any periodic element of X is Besicovitch almost periodic. Clearly, elements with different periods will not be generic with respect to the same measure. This motivates the following definition.
Definition 4.5. (Generic Besicovitch almost periodic points)
Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence on G. Then, for any invariant probability measure m on
$(B_n)$
be a Følner sequence on G. Then, for any invariant probability measure m on
![]() $(X,G)$
, we denote by
$(X,G)$
, we denote by
![]() $\mathrm {Bap} (X,G,m)$
the set of those Besicovitch almost periodic points which are generic with respect to m.
$\mathrm {Bap} (X,G,m)$
the set of those Besicovitch almost periodic points which are generic with respect to m.
We have the following consequence of the preceding theorem.
Proposition 4.6. Let
![]() $(X,G,m)$
be a dynamical system and let
$(X,G,m)$
be a dynamical system and let
![]() $(B_n)$
be a Følner sequence. Then,
$(B_n)$
be a Følner sequence. Then,
![]() $\mathrm {Bap} (X,G,m)$
is a measurable invariant set.
$\mathrm {Bap} (X,G,m)$
is a measurable invariant set.
Proof. Clearly,
![]() $\mathrm {Bap} (X,G,m)$
is invariant as both the set of generic points and the set of Besicovitch almost periodic points are invariant. If
$\mathrm {Bap} (X,G,m)$
is invariant as both the set of generic points and the set of Besicovitch almost periodic points are invariant. If
![]() $\mathrm {Bap} (X,G,m)$
is empty, there is nothing left to show. Thus, consider the case
$\mathrm {Bap} (X,G,m)$
is empty, there is nothing left to show. Thus, consider the case
![]() $\mathrm {Bap}(X,G,m)\neq \varnothing $
. By Theorem 4.4, the dynamical system
$\mathrm {Bap}(X,G,m)\neq \varnothing $
. By Theorem 4.4, the dynamical system
![]() $(X,G,m)$
then has pure point spectrum and the set of its eigenvalues
$(X,G,m)$
then has pure point spectrum and the set of its eigenvalues
![]() $\mathrm {Eig}(X,G,m)$
equals
$\mathrm {Eig}(X,G,m)$
equals
![]() $\mathrm {Freq}(p)$
for any
$\mathrm {Freq}(p)$
for any
![]() $p\in \mathrm {Bap}(X,G,m)$
. Set
$p\in \mathrm {Bap}(X,G,m)$
. Set
![]() $E:= \mathrm {Eig}(X,G,m)$
.
$E:= \mathrm {Eig}(X,G,m)$
.
Claim. Let D be a dense subset of
![]() $C(X)$
. Then, we have
$C(X)$
. Then, we have
![]() $p\in \mathrm {Bap}(X,G,m)$
if and only if the following three points hold:
$p\in \mathrm {Bap}(X,G,m)$
if and only if the following three points hold:
-
•
 $A(f_p)$
exists and equals
$A(f_p)$
exists and equals
 $\int _X f\,d m$
for all
$\int _X f\,d m$
for all
 $f\in D$
;
$f\in D$
; -
•
 $A(f_p \overline {\xi })$
exists for all
$A(f_p \overline {\xi })$
exists for all
 $\xi \in E$
and
$\xi \in E$
and
 $f\in D$
;
$f\in D$
; -
•
 $A(|f_p|^2) = \sum _{\xi \in E} |A(f_p\overline {\xi })|^2$
for all
$A(|f_p|^2) = \sum _{\xi \in E} |A(f_p\overline {\xi })|^2$
for all
 $f\in D$
.
$f\in D$
.
Proof of claim
Consider
![]() $p\in \mathrm {Bap} (X,G,m)$
. Then, p is generic and the first point holds (even for all
$p\in \mathrm {Bap} (X,G,m)$
. Then, p is generic and the first point holds (even for all
![]() $f\in C(X)$
). In particular,
$f\in C(X)$
). In particular,
![]() $A(|f_p|^2)$
exists. Now, the second and third point follow from Proposition 4.2 as p is Besicovitch almost periodic with set of frequencies given by E.
$A(|f_p|^2)$
exists. Now, the second and third point follow from Proposition 4.2 as p is Besicovitch almost periodic with set of frequencies given by E.
Consider now a
![]() $p\in X$
satisfying the three points in the claim. By density of D in
$p\in X$
satisfying the three points in the claim. By density of D in
![]() $C(X)$
, we then easily infer that
$C(X)$
, we then easily infer that
![]() $A(f_p) = \int _X f\,d m$
holds for all
$A(f_p) = \int _X f\,d m$
holds for all
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $A(f_p \overline {\xi })$
exists for all
$A(f_p \overline {\xi })$
exists for all
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\xi \in E$
. In particular, we have
$\xi \in E$
. In particular, we have
![]() $A(|f_p|^2) = \int |f|^2\,d m$
for all
$A(|f_p|^2) = \int |f|^2\,d m$
for all
![]() $f\in C(X)$
. Given this, we can now follow the proof of Theorem 4.4 to conclude the existence of (pairwise orthogonal) eigenfunctions
$f\in C(X)$
. Given this, we can now follow the proof of Theorem 4.4 to conclude the existence of (pairwise orthogonal) eigenfunctions
![]() $e_\xi $
to
$e_\xi $
to
![]() $\xi \in \mathrm {Eig}(X,G,m)$
with
$\xi \in \mathrm {Eig}(X,G,m)$
with
![]() $\|e_\xi \|\leq 1$
and
$\|e_\xi \|\leq 1$
and
 $$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 = \int_X |f|^2\,d m \end{align*} $$
$$ \begin{align*} \sum_{\xi\in E} \bigg| \int_X f\, \overline{e_\xi}\,d m\bigg|^2 = \int_X |f|^2\,d m \end{align*} $$
for all
![]() $f\in D$
. As D is dense, this is only possible if
$f\in D$
. As D is dense, this is only possible if
![]() $\|e_\xi \|=1$
holds for all
$\|e_\xi \|=1$
holds for all
![]() $\xi \in E$
and the
$\xi \in E$
and the
![]() $e_\xi $
,
$e_\xi $
,
![]() $\xi \in E$
, are an orthonormal basis. This finishes the proof of the claim.
$\xi \in E$
, are an orthonormal basis. This finishes the proof of the claim.
Given the claim, the desired measurability follows easily: by compactness and metrizability of X we can choose a countable dense subset D of
![]() $C(X)$
. Then, the claim gives that
$C(X)$
. Then, the claim gives that
![]() $p\in X$
belongs to
$p\in X$
belongs to
![]() $\mathrm {Bap} (X,G,m)$
if countably many conditions are satisfied. Clearly, each of these conditions gives a measurable set.
$\mathrm {Bap} (X,G,m)$
if countably many conditions are satisfied. Clearly, each of these conditions gives a measurable set.
The following theorem can be seen as both a converse to Theorem 4.4 and an analog to Theorem 3.8.
Theorem 4.7. (Discrete spectrum via Besicovitch almost periodic points)
Let
![]() $(X,G,m)$
be an ergodic dynamical system and let
$(X,G,m)$
be an ergodic dynamical system and let
![]() $(B_n)$
be a Følner sequence along which Birkhoff’s ergodic theorem holds. Then, the following assertions are equivalent.
$(B_n)$
be a Følner sequence along which Birkhoff’s ergodic theorem holds. Then, the following assertions are equivalent.
-
(i) The dynamical system
 $(X,G,m)$
has pure point spectrum.
$(X,G,m)$
has pure point spectrum. -
(ii)
 $m(\mathrm {Bap}(X,G,m)) =1$
.
$m(\mathrm {Bap}(X,G,m)) =1$
. -
(iii)
 $\mathrm {Bap} (X,G,m)\neq \varnothing $
.
$\mathrm {Bap} (X,G,m)\neq \varnothing $
.
If one of the equivalent conditions (i), (ii) and (iii) holds, then
![]() $\mathrm {Eig}(X,G,m) = \mathrm {Freq}(x)$
for every
$\mathrm {Eig}(X,G,m) = \mathrm {Freq}(x)$
for every
![]() $x\in \mathrm {Bap}(X,G,m)$
. Moreover, in this case, for any
$x\in \mathrm {Bap}(X,G,m)$
. Moreover, in this case, for any
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\xi \in \widehat {G}$
the function
$\xi \in \widehat {G}$
the function
 $$ \begin{align*} e_{f,\xi} : X\longrightarrow \mathbb{C}, \quad e_{f,\xi}(x) :=\left\{\begin{array}{@{}l@{}l} \mathrm{A}(f_x \overline{\xi}), &\quad x\in \mathrm{Bap} (X,G,m),\\ 0, &\quad \mbox{otherwise,} \end{array} \right. \end{align*} $$
$$ \begin{align*} e_{f,\xi} : X\longrightarrow \mathbb{C}, \quad e_{f,\xi}(x) :=\left\{\begin{array}{@{}l@{}l} \mathrm{A}(f_x \overline{\xi}), &\quad x\in \mathrm{Bap} (X,G,m),\\ 0, &\quad \mbox{otherwise,} \end{array} \right. \end{align*} $$
satisfies
![]() $P_\xi f = e_{f,\xi }$
(in
$P_\xi f = e_{f,\xi }$
(in
![]() $L^2 (X,m)$
),
$L^2 (X,m)$
),
![]() $e_{f,\xi } (tx) = \xi (t) e_{f,\xi }(x)$
for all
$e_{f,\xi } (tx) = \xi (t) e_{f,\xi }(x)$
for all
![]() $t\in G$
and
$t\in G$
and
![]() $x\in X$
and has constant modulus on
$x\in X$
and has constant modulus on
![]() $\mathrm {Bap} (X,G,m)$
.
$\mathrm {Bap} (X,G,m)$
.
Remark. By Theorem 4.4, the existence of a generic Besicovitch almost periodic point entails the ergodicity of m. For this reason, the ergodicity assumption in the above theorem cannot be dropped.
Proof. The implication (ii)
![]() $\Longrightarrow $
(iii) is clear. The implication (iii)
$\Longrightarrow $
(iii) is clear. The implication (iii)
![]() $\Longrightarrow $
(i) follows from Theorem 4.4. We now show (i)
$\Longrightarrow $
(i) follows from Theorem 4.4. We now show (i)
![]() $\Longrightarrow $
(ii). As the set of generic points has full measure, it suffices to show that almost every
$\Longrightarrow $
(ii). As the set of generic points has full measure, it suffices to show that almost every
![]() $x\in X$
is Besicovitch almost periodic. To do so, we denote the inner product on
$x\in X$
is Besicovitch almost periodic. To do so, we denote the inner product on
![]() $L^2 (X,m)$
by
$L^2 (X,m)$
by
![]() $\langle \cdot ,\cdot \rangle $
and the associated norm by
$\langle \cdot ,\cdot \rangle $
and the associated norm by
![]() $\|\cdot \|_2$
. Let
$\|\cdot \|_2$
. Let
![]() $\xi _1,\xi _2,\xi _3,\ldots , $
be an enumeration of
$\xi _1,\xi _2,\xi _3,\ldots , $
be an enumeration of
![]() $\mathrm {Eig}(X,G,m)$
. Choose for any
$\mathrm {Eig}(X,G,m)$
. Choose for any
![]() $\xi \in E$
a normalized eigenfunction
$\xi \in E$
a normalized eigenfunction
![]() $e_\xi : X\longrightarrow \mathbb {C}$
. Without loss of generality, we can assume
$e_\xi : X\longrightarrow \mathbb {C}$
. Without loss of generality, we can assume
for all
![]() $s\in G$
and
$s\in G$
and
![]() $x\in X$
. (Otherwise, we could replace
$x\in X$
. (Otherwise, we could replace
![]() $e_\xi $
by
$e_\xi $
by
![]() $\widetilde {e}_\xi $
defined by
$\widetilde {e}_\xi $
defined by
 $$ \begin{align*} \widetilde{e}_\xi(x) :=\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} e(sx)\, \overline{\xi}(s)\,d s \end{align*} $$
$$ \begin{align*} \widetilde{e}_\xi(x) :=\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} e(sx)\, \overline{\xi}(s)\,d s \end{align*} $$
if the limit exists and
![]() $\widetilde {e}_\xi (x) =0$
otherwise.) Moreover, for
$\widetilde {e}_\xi (x) =0$
otherwise.) Moreover, for
![]() $\xi = 1$
we choose the constant function
$\xi = 1$
we choose the constant function
![]() $1$
.
$1$
.
Consider now an arbitrary
![]() $g\in C(X)$
. By Birkhoff’s ergodic theorem, we can then find a subset
$g\in C(X)$
. By Birkhoff’s ergodic theorem, we can then find a subset
![]() $X_g$
of X of full measure such that
$X_g$
of X of full measure such that
 $$ \begin{align*} \int_X \bigg|g - \sum_{j=1}^k \langle g,e_{\xi_j} \rangle e_{\xi_j}\bigg|\,d m(x) = \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|g(sx) - \sum_{j=1}^k \langle g,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s \end{align*} $$
$$ \begin{align*} \int_X \bigg|g - \sum_{j=1}^k \langle g,e_{\xi_j} \rangle e_{\xi_j}\bigg|\,d m(x) = \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|g(sx) - \sum_{j=1}^k \langle g,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s \end{align*} $$
for all
![]() $x\in X_g$
and
$x\in X_g$
and
![]() $k\in \mathbb {N}$
. Let
$k\in \mathbb {N}$
. Let
![]() $D\subset C(X)$
be a countable dense subset. Define
$D\subset C(X)$
be a countable dense subset. Define
 $$ \begin{align*}X':=\bigcap_{g\in D} X_g.\end{align*} $$
$$ \begin{align*}X':=\bigcap_{g\in D} X_g.\end{align*} $$
Then,
![]() $X'$
has full measure and a short computation gives
$X'$
has full measure and a short computation gives
 $$ \begin{align*} \int_X \bigg|f - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg|\,d m(x) = \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(sx) - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s \end{align*} $$
$$ \begin{align*} \int_X \bigg|f - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg|\,d m(x) = \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(sx) - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s \end{align*} $$
for all
![]() $f\in C(X)$
,
$f\in C(X)$
,
![]() $x\in X'$
and
$x\in X'$
and
![]() $k\in \mathbb {N}$
. This, in turn, implies that any
$k\in \mathbb {N}$
. This, in turn, implies that any
![]() $x\in X'$
is Besicovitch almost periodic: indeed, a short calculation invoking Birkhoff’s ergodic theorem and the Cauchy–Schwarz inequality shows
$x\in X'$
is Besicovitch almost periodic: indeed, a short calculation invoking Birkhoff’s ergodic theorem and the Cauchy–Schwarz inequality shows
 $$ \begin{align*} \overline{M}\bigg( \bigg|f(\cdot x) -\sum_{j=1}^k \langle f, e_{\xi_j} \rangle\, e_{\xi_j}(x)\, \xi_j (\cdot)\bigg|\bigg) &= \overline{M}\bigg( \bigg|f(\cdot x) -\sum_{j=1}^k \langle f, e_{\xi_j} \rangle\, e_{\xi_j}(\cdot x)\bigg|\bigg)\\ (\mbox{Birkhoff's ergodic theorem})&= \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(sx) - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s\\ &= \int_X \bigg|f - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg|\,d m(x)\\ (\mbox{Cauchy--Schwarz inequality})& \leq \bigg\|f -\sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg\|_2\\ &\to 0, n\to \infty. \end{align*} $$
$$ \begin{align*} \overline{M}\bigg( \bigg|f(\cdot x) -\sum_{j=1}^k \langle f, e_{\xi_j} \rangle\, e_{\xi_j}(x)\, \xi_j (\cdot)\bigg|\bigg) &= \overline{M}\bigg( \bigg|f(\cdot x) -\sum_{j=1}^k \langle f, e_{\xi_j} \rangle\, e_{\xi_j}(\cdot x)\bigg|\bigg)\\ (\mbox{Birkhoff's ergodic theorem})&= \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(sx) - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j} (sx)\bigg|\,d s\\ &= \int_X \bigg|f - \sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg|\,d m(x)\\ (\mbox{Cauchy--Schwarz inequality})& \leq \bigg\|f -\sum_{j=1}^k \langle f,e_{\xi_j}\rangle e_{\xi_j}\bigg\|_2\\ &\to 0, n\to \infty. \end{align*} $$
This gives the desired claim.
We now turn to the remaining statements. The equality
![]() $\mathrm {Freq} (x) = \mathrm {Eig}(X,G,m)$
for an element
$\mathrm {Freq} (x) = \mathrm {Eig}(X,G,m)$
for an element
![]() $x\in \mathrm {Bap} (X,G,m)$
directly follows from Theorem 4.4. As for
$x\in \mathrm {Bap} (X,G,m)$
directly follows from Theorem 4.4. As for
![]() $e_{f,\xi }$
, we note that it is well defined and invariant (as
$e_{f,\xi }$
, we note that it is well defined and invariant (as
![]() $\mathrm {Bap}(X,G,m)$
is invariant). The equality
$\mathrm {Bap}(X,G,m)$
is invariant). The equality
![]() $\mathrm {Freq} (x) = \mathrm {Eig}(X,G,m)$
for
$\mathrm {Freq} (x) = \mathrm {Eig}(X,G,m)$
for
![]() $x\in \mathrm {Bap} (X,G,m)$
rather directly gives that
$x\in \mathrm {Bap} (X,G,m)$
rather directly gives that
![]() $e_{f,\xi }$
vanishes identically for
$e_{f,\xi }$
vanishes identically for
![]() $\xi \in \widehat {G}\setminus \mathrm {Eig}(X,G,m)$
. In particular, it has constant modulus on
$\xi \in \widehat {G}\setminus \mathrm {Eig}(X,G,m)$
. In particular, it has constant modulus on
![]() $\mathrm {Bap}(X,G,m)$
. Now, by Theorem 4.4, for each
$\mathrm {Bap}(X,G,m)$
. Now, by Theorem 4.4, for each
![]() $\xi \in E$
and
$\xi \in E$
and
![]() $x\in \mathrm {Bap} (X,G,m)$
there exists a normalized eigenfunction
$x\in \mathrm {Bap} (X,G,m)$
there exists a normalized eigenfunction
![]() $e_\xi ^{(x)}$
with
$e_\xi ^{(x)}$
with
As each eigenspace is one dimensional, the
![]() $e_\xi ^{(x)}$
arising for different
$e_\xi ^{(x)}$
arising for different
![]() $x\in \mathrm {Bap}(X,G,m)$
will only differ by a factor of modulus one. This gives the statement on constancy of the modulus.
$x\in \mathrm {Bap}(X,G,m)$
will only differ by a factor of modulus one. This gives the statement on constancy of the modulus.
That
![]() $e_{f,\xi }$
is the projection onto the eigenspace of
$e_{f,\xi }$
is the projection onto the eigenspace of
![]() $\xi $
follows from standard theory; see, e.g., [Reference Lenz27] for a recent discussion.
$\xi $
follows from standard theory; see, e.g., [Reference Lenz27] for a recent discussion.
5 Weyl almost periodic points, unique ergodicity and continuity of eigenfunctions
In this section, we consider a strengthening of Besicovitch almost periodicity, namely Weyl almost periodicity. We show that Weyl almost periodicity extends from one point to its orbit closure. This allows us to characterize transitive systems all of whose points are Weyl almost periodic. These are exactly the uniquely ergodic dynamical systems with pure point spectrum and continuous eigenfunctions. This ties in with various recent investigations (see the following for details).
Let
![]() $(X,G)$
be a dynamical system. Whenever d is a metric on X generating the topology and
$(X,G)$
be a dynamical system. Whenever d is a metric on X generating the topology and
![]() $(B_n)$
is a Følner sequence, we define for each
$(B_n)$
is a Følner sequence, we define for each
![]() $n\in \mathbb {N}$
the map
$n\in \mathbb {N}$
the map
 $$ \begin{align*} \overline{M}_n :B(G) \longrightarrow \mathbb{R},\quad \overline{M}_n (f):=\sup_{s\in G} \frac{1}{|B_n|} \int_{B_n +s} f(t)\,d t. \end{align*} $$
$$ \begin{align*} \overline{M}_n :B(G) \longrightarrow \mathbb{R},\quad \overline{M}_n (f):=\sup_{s\in G} \frac{1}{|B_n|} \int_{B_n +s} f(t)\,d t. \end{align*} $$
This gives then rise to the functions
for each
![]() $n\in \mathbb {N}$
. Then, each
$n\in \mathbb {N}$
. Then, each
![]() $D_n$
can easily be seen to be an invariant metric. Moreover, for each
$D_n$
can easily be seen to be an invariant metric. Moreover, for each
![]() $x\in X$
the function
$x\in X$
the function
![]() $t\mapsto D_n (x,tx)$
is uniformly continuous (by the argument used in §2 to show uniform continuity of D). The function
$t\mapsto D_n (x,tx)$
is uniformly continuous (by the argument used in §2 to show uniform continuity of D). The function
![]() $D_n$
is referred to as the averaged metric on level n.
$D_n$
is referred to as the averaged metric on level n.
A bounded measurable function
![]() $f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if for each
$f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if for each
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k \in \widehat {G}$
and
$\xi _1,\ldots , \xi _k \in \widehat {G}$
and
![]() $c_1,\ldots ,c_k\in \mathbb {C}$
with
$c_1,\ldots ,c_k\in \mathbb {C}$
with
 $$ \begin{align*}\limsup_{n\to \infty} \overline{M}_n \bigg(\bigg|f - \sum_{j=1}^k c_{j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
$$ \begin{align*}\limsup_{n\to \infty} \overline{M}_n \bigg(\bigg|f - \sum_{j=1}^k c_{j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
As discussed in Appendix D, an equivalent alternative characterization is that for each
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $N\in \mathbb {N}$
and a relatively dense set
$N\in \mathbb {N}$
and a relatively dense set
![]() $R\subset G$
with
$R\subset G$
with
for all
![]() $t\in R$
. A crucial feature of Weyl almost periodic functions is the existence of the limits
$t\in R$
. A crucial feature of Weyl almost periodic functions is the existence of the limits
 $$ \begin{align*} \lim_{n\to\infty} \frac{1}{|B_n|} \int_{B_n + s_n} f(t)\, \xi (t)\,d t \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \frac{1}{|B_n|} \int_{B_n + s_n} f(t)\, \xi (t)\,d t \end{align*} $$
irrespective of (and uniform in) the chosen sequence
![]() $(s_n)\in G$
for each
$(s_n)\in G$
for each
![]() $\xi \in \widehat {G}$
, see Appendix D.
$\xi \in \widehat {G}$
, see Appendix D.
Definition 5.1. (Weyl almost periodic points)
Let
![]() $(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
$(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
![]() $(B_n)$
be a Følner sequence and let
$(B_n)$
be a Følner sequence and let
![]() $D_n$
,
$D_n$
,
![]() $n\in \mathbb {N}$
, be the associated averaged metrics. Then, a point
$n\in \mathbb {N}$
, be the associated averaged metrics. Then, a point
![]() $x\in X$
is called Weyl almost periodic with respect to d and
$x\in X$
is called Weyl almost periodic with respect to d and
![]() $(B_n)$
if for every
$(B_n)$
if for every
![]() $\varepsilon>0$
there exists an
$\varepsilon>0$
there exists an
![]() $N\in \mathbb {N}$
such that
$N\in \mathbb {N}$
such that
is relatively dense.
Remark. It follows from Proposition D.1 that an
![]() $x\in X$
is Weyl almost periodic if and only if for each
$x\in X$
is Weyl almost periodic if and only if for each
![]() $\varepsilon>0$
there exists a relatively dense set
$\varepsilon>0$
there exists a relatively dense set
![]() $R\subset G$
and an
$R\subset G$
and an
![]() $N_0\in \mathbb {N}$
such that
$N_0\in \mathbb {N}$
such that
![]() $D_N (x,tx)<\varepsilon $
for all
$D_N (x,tx)<\varepsilon $
for all
![]() $N\geq N_0$
and
$N\geq N_0$
and
![]() $t\in R$
.
$t\in R$
.
Arguing as in §3 with
![]() $\overline {M}$
replaced by
$\overline {M}$
replaced by
![]() $\overline {M}_n$
we see that Weyl almost periodicity is independent of the chosen metric and the following holds.
$\overline {M}_n$
we see that Weyl almost periodicity is independent of the chosen metric and the following holds.
Lemma 5.2. Let
![]() $(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
$(X,G)$
be a dynamical system, let d be a metric on X generating the topology, let
![]() $(B_n)$
be a Følner sequence and let
$(B_n)$
be a Følner sequence and let
![]() $D_n$
,
$D_n$
,
![]() $n\in \mathbb {N}$
, be the associated averaged metrics. Then, the following assertions for
$n\in \mathbb {N}$
, be the associated averaged metrics. Then, the following assertions for
![]() $x\in X$
are equivalent.
$x\in X$
are equivalent.
-
(i) The point x is Weyl almost periodic.
-
(ii) The algebra
 $\mathcal {A}_x$
consists of Weyl almost periodic functions.
$\mathcal {A}_x$
consists of Weyl almost periodic functions. -
(iii) The set
 $\{f\in C(X): f_x \mbox { is Weyl almost periodic} \}$
separates the points of X.
$\{f\in C(X): f_x \mbox { is Weyl almost periodic} \}$
separates the points of X. -
(iv) For any
 $s\in G$
the function
$s\in G$
the function
 $d^{(s)}_x$
is Weyl almost periodic, where
$d^{(s)}_x$
is Weyl almost periodic, where
 $d^{(s)} \in C(X)$
is defined via
$d^{(s)} \in C(X)$
is defined via
 $d^{(s)}(y) : =d(sx,y)$
.
$d^{(s)}(y) : =d(sx,y)$
.
The previous lemma implies, in particular, that any Weyl almost periodic point is Besicovitch almost periodic. It is not hard to see by examples that the converse does not hold.
Weyl almost periodicity has a stability property.
Lemma 5.3. (Stability of Weyl almost periodicity along orbit closures)
Let
![]() $(X,G)$
be a dynamical system. Assume that
$(X,G)$
be a dynamical system. Assume that
![]() $x\in X$
is Weyl almost periodic. Then, any element in the orbit closure of x is Weyl almost periodic.
$x\in X$
is Weyl almost periodic. Then, any element in the orbit closure of x is Weyl almost periodic.
Proof. The function
![]() $D_N$
is lower semi-continuous for each
$D_N$
is lower semi-continuous for each
![]() $N\in \mathbb {N}$
as it is a supremum over continuous functions. From this and the invariance of
$N\in \mathbb {N}$
as it is a supremum over continuous functions. From this and the invariance of
![]() $D_N$
we find
$D_N$
we find
whenever
![]() $s_n x\to y$
for a sequence
$s_n x\to y$
for a sequence
![]() $(s_n)$
in G. This easily gives the desired statement.
$(s_n)$
in G. This easily gives the desired statement.
Proposition 5.4. Let
![]() $(X,G)$
be a dynamical system with transitive element
$(X,G)$
be a dynamical system with transitive element
![]() $p\in X$
. Let p be Weyl almost periodic. Then
$p\in X$
. Let p be Weyl almost periodic. Then
![]() $(X,G)$
is uniquely ergodic, has pure point spectrum, all eigenfunctions are continuous and
$(X,G)$
is uniquely ergodic, has pure point spectrum, all eigenfunctions are continuous and
![]() $\mathrm {Freq}(x) = \mathrm {Eig}(X,G,m)$
holds for all
$\mathrm {Freq}(x) = \mathrm {Eig}(X,G,m)$
holds for all
![]() $x\in X$
. Moreover, for any
$x\in X$
. Moreover, for any
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\xi \in \widehat {G}$
, the averages
$\xi \in \widehat {G}$
, the averages
 $$ \begin{align*} A_n (f_x\overline{\xi}):=\frac{1}{B_n} \int_{B_n} f(tx)\, \overline{\xi(t)}\,d t \end{align*} $$
$$ \begin{align*} A_n (f_x\overline{\xi}):=\frac{1}{B_n} \int_{B_n} f(tx)\, \overline{\xi(t)}\,d t \end{align*} $$
converge (uniformly in x) towards the projection of f onto the eigenspace of
![]() $\xi $
.
$\xi $
.
Proof. It is well known that unique ergodicity is equivalent to uniform (in
![]() $y\in X$
) convergence of the averages
$y\in X$
) convergence of the averages
 $$ \begin{align*} \frac{1}{|B_n|} \int_{B_n} f(ty)\,d t \end{align*} $$
$$ \begin{align*} \frac{1}{|B_n|} \int_{B_n} f(ty)\,d t \end{align*} $$
for each continuous
![]() $f:X\longrightarrow \mathbb {C}$
. Now, uniform existence of these averages on the orbit of x is a direct consequence of Weyl almost periodicity. This easily gives uniform existence on the orbit closure. As the orbit closure is X the desired statement on unique ergodicity follows. Denote the unique invariant probability measure by m.
$f:X\longrightarrow \mathbb {C}$
. Now, uniform existence of these averages on the orbit of x is a direct consequence of Weyl almost periodicity. This easily gives uniform existence on the orbit closure. As the orbit closure is X the desired statement on unique ergodicity follows. Denote the unique invariant probability measure by m.
By the previous lemma and the transitivity assumption on p, every
![]() $x\in X$
is Weyl almost periodic. In particular, every element is Besicovitch almost periodic. As
$x\in X$
is Weyl almost periodic. In particular, every element is Besicovitch almost periodic. As
![]() $(X,G)$
is uniquely ergodic every
$(X,G)$
is uniquely ergodic every
![]() $x\in X$
is also generic with respect to m. Hence,
$x\in X$
is also generic with respect to m. Hence,
![]() $X=\mathrm {Bap}(X,G,m)$
follows. By Theorem 4.7, this implies pure point spectrum as well as pointwise convergence of the averages
$X=\mathrm {Bap}(X,G,m)$
follows. By Theorem 4.7, this implies pure point spectrum as well as pointwise convergence of the averages
![]() $A_n (f_x\overline {\xi })$
to the projection of f onto the eigenspace of
$A_n (f_x\overline {\xi })$
to the projection of f onto the eigenspace of
![]() $\xi $
for each
$\xi $
for each
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $\xi \in \widehat {G}$
. Now, by Weyl almost periodicity these averages converge uniformly in
$\xi \in \widehat {G}$
. Now, by Weyl almost periodicity these averages converge uniformly in
![]() $x\in X$
. Hence, their limit is continuous and continuity of the eigenfunctions follows.
$x\in X$
. Hence, their limit is continuous and continuity of the eigenfunctions follows.
Theorem 5.5. Let
![]() $(X,G)$
be a dynamical system with transitive point
$(X,G)$
be a dynamical system with transitive point
![]() $p\in X$
. Then, the following assertions are equivalent.
$p\in X$
. Then, the following assertions are equivalent.
-
(i) The dynamical system
 $(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
$(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions. -
(ii) The point p is Weyl almost periodic.
-
(iii) Every
 $x \in X$
is Weyl almost periodic.
$x \in X$
is Weyl almost periodic.
In this case, we have
![]() $\mathrm {Freq}(x) = \mathrm {Eig}(X,G,m)$
for all
$\mathrm {Freq}(x) = \mathrm {Eig}(X,G,m)$
for all
![]() $x\in X$
.
$x\in X$
.
Proof. The implication (iii)
![]() $\Longrightarrow $
(ii) is obvious whereas (ii)
$\Longrightarrow $
(ii) is obvious whereas (ii)
![]() $\Longrightarrow $
(iii) follows from Lemma 5.3.
$\Longrightarrow $
(iii) follows from Lemma 5.3.
The implication (ii)
![]() $\Longrightarrow $
(i) and the last part of the theorem were shown in Proposition 5.4. It remains to show the reverse implication (i)
$\Longrightarrow $
(i) and the last part of the theorem were shown in Proposition 5.4. It remains to show the reverse implication (i)
![]() $\Longrightarrow $
(ii): this follows by a variant of the proof of the corresponding part in Theorem 4.7. We denote the unique invariant measure by m and use the notation introduced in the proof of Theorem 4.7. Thus, we denote the inner product on
$\Longrightarrow $
(ii): this follows by a variant of the proof of the corresponding part in Theorem 4.7. We denote the unique invariant measure by m and use the notation introduced in the proof of Theorem 4.7. Thus, we denote the inner product on
![]() $L^2 (X,m)$
by
$L^2 (X,m)$
by
![]() $\langle \cdot ,\cdot \rangle $
and the associated norm by
$\langle \cdot ,\cdot \rangle $
and the associated norm by
![]() $\|\cdot \|_2$
. As the spectrum is pure point, there exists an orthonormal basis
$\|\cdot \|_2$
. As the spectrum is pure point, there exists an orthonormal basis
![]() $e_\xi $
,
$e_\xi $
,
![]() $\xi \in \mathrm {Eig}(X,G,m)$
, of
$\xi \in \mathrm {Eig}(X,G,m)$
, of
![]() $L^2 (X,m)$
with
$L^2 (X,m)$
with
![]() $e_\xi $
being an eigenfunction to the eigenvalue
$e_\xi $
being an eigenfunction to the eigenvalue
![]() $\xi $
for each
$\xi $
for each
![]() $\xi \in \mathrm {Eig}(X,G,m)$
. By assumption, each
$\xi \in \mathrm {Eig}(X,G,m)$
. By assumption, each
![]() $e_\xi $
,
$e_\xi $
,
![]() $\xi \in E$
, can be chosen continuous. By unique ergodicity, we then find for any finite subset
$\xi \in E$
, can be chosen continuous. By unique ergodicity, we then find for any finite subset
![]() $A\subset \mathrm {Eig}(X,G,m)$
and any
$A\subset \mathrm {Eig}(X,G,m)$
and any
![]() $y\in X$
:
$y\in X$
:
 $$ \begin{align*} \limsup_{n\to\infty} \overline{M}_n\bigg(\bigg|f(\cdot y) - \sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (y) \xi (\cdot)\bigg|\bigg)&= \limsup_{n\to\infty} \overline{M}_n \bigg|f(\cdot y) - \sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (\cdot y)\bigg|\\ & = \lim_{n\to\infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(ty)\\ &\quad-\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (t y)\bigg|\,d t\\ & = \int_X \bigg| f(x) -\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} ( x)\bigg|\,d m(x)\\ (\mbox{Cauchy--Schwarz inequality})&\leq \bigg\|f -\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} \bigg\|_2. \end{align*} $$
$$ \begin{align*} \limsup_{n\to\infty} \overline{M}_n\bigg(\bigg|f(\cdot y) - \sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (y) \xi (\cdot)\bigg|\bigg)&= \limsup_{n\to\infty} \overline{M}_n \bigg|f(\cdot y) - \sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (\cdot y)\bigg|\\ & = \lim_{n\to\infty}\frac{1}{|B_n|} \int_{B_n} \bigg|f(ty)\\ &\quad-\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} (t y)\bigg|\,d t\\ & = \int_X \bigg| f(x) -\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} ( x)\bigg|\,d m(x)\\ (\mbox{Cauchy--Schwarz inequality})&\leq \bigg\|f -\sum_{\xi \in A} \langle e_{\xi}, f\rangle e_{\xi} \bigg\|_2. \end{align*} $$
As
![]() $f_\xi $
,
$f_\xi $
,
![]() $\xi \in E$
, is a basis of
$\xi \in E$
, is a basis of
![]() $L^2 (X,m)$
, the last term becomes arbitrarily small for suitable
$L^2 (X,m)$
, the last term becomes arbitrarily small for suitable
![]() $A\subset E$
. This shows that
$A\subset E$
. This shows that
![]() $t\mapsto f(ty)$
is Weyl almost periodic for any
$t\mapsto f(ty)$
is Weyl almost periodic for any
![]() $y\in X$
.
$y\in X$
.
Remark. Recently, systems satisfying the equivalent conditions of the theorem have attracted substantial interest.
-
(a) For
 $G = \mathbb {Z}$
various equivalent characterizations of assertion (i) have been investigated in [Reference Downarowicz and Glasner11]. In particular, it is shown there that assertion (i) is equivalent to the topological isomorphy of the system to its maximal equicontinuous factor. The case of general amenable groups G has been studied in [Reference Fuhrmann, Gröger and Lenz16]. In particular, it has been shown there that assertion (i) is equivalent to the continuity of the averaged metric D on
$G = \mathbb {Z}$
various equivalent characterizations of assertion (i) have been investigated in [Reference Downarowicz and Glasner11]. In particular, it is shown there that assertion (i) is equivalent to the topological isomorphy of the system to its maximal equicontinuous factor. The case of general amenable groups G has been studied in [Reference Fuhrmann, Gröger and Lenz16]. In particular, it has been shown there that assertion (i) is equivalent to the continuity of the averaged metric D on
 $X\times X$
. This continuity is known as mean equicontinuity of the system. In this context our preceding result is remarkable as it does not assume control of D on the whole of
$X\times X$
. This continuity is known as mean equicontinuity of the system. In this context our preceding result is remarkable as it does not assume control of D on the whole of
 $X\times X$
but just on
$X\times X$
but just on
 $\{(x,tx) : t\in G\}$
. In this sense, we have found a pointwise characterization of mean equicontinuity. Note, however, that we require a rather uniform control on the orbit of this one point.
$\{(x,tx) : t\in G\}$
. In this sense, we have found a pointwise characterization of mean equicontinuity. Note, however, that we require a rather uniform control on the orbit of this one point.Note that [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16] also study Besicovitch and Weyl-type averages and metrics defined by them. It then turns out that for the continuity of some maps with respect to these metrics (mean equicontinuity) it is not relevant whether the Besicovitch or the Weyl-type average is considered. This is very different from our previous considerations. The reason is that the continuity condition in [Reference Downarowicz and Glasner11, Reference Fuhrmann, Gröger and Lenz16] involves all points of the dynamical system and this then implies unique ergodicity, which ensures uniform behavior of all points.
-
(b) A large class of examples satisfying the conditions of the theorem are weakly almost periodic systems. A recent study of such systems is carried out in [Reference Lenz and Strungaru33] to which we refer for a precise definition and further references, see also §6.
-
(c) A most important class of examples for the theorem are dynamical systems arising from regular cut and project schemes. Such systems are at the core of the study of aperiodic order (see [Reference Baake and Grimm2]). They belong to the special class of dynamical systems known as translation-bounded measure dynamical systems (TMDSs), see §7 for details. In fact, a huge bulk of material in the theory of aperiodic order deals with TMDSs satisfying assertion (i) of the theorem. A characterization of such systems via an almost periodicity property of its points had been missing for a long time. It was only given recently in [Reference Lenz, Spindeler and Strungaru31]. The preceding theorem is a generalization of the corresponding result of [Reference Lenz, Spindeler and Strungaru31] in that it is not restricted to TMDSs but rather applies to general dynamical systems.
If a system is minimal every point is transitive and we can note the following immediate consequence of the preceding theorem.
Corollary 5.6. Let
![]() $(X,G)$
be a minimal dynamical system. Then, the following assertions are equivalent.
$(X,G)$
be a minimal dynamical system. Then, the following assertions are equivalent.
-
(i) Every point in X is Weyl almost periodic.
-
(ii) There exists a Weyl almost periodic point in X.
-
(iii) The dynamical system
 $(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
$(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
Remark. A system can well be Weyl almost periodic without being minimal. Consider, for example, the orbit closure in the subshift
![]() $(\{0,1\}^{\mathbb {Z}},\mathbb {Z})$
of the element
$(\{0,1\}^{\mathbb {Z}},\mathbb {Z})$
of the element
![]() $\omega $
defined with
$\omega $
defined with
![]() $\omega _0 = 1$
and
$\omega _0 = 1$
and
![]() $\omega _n = 0$
for
$\omega _n = 0$
for
![]() $n\neq 0$
.
$n\neq 0$
.
6 Weakly and Bohr almost periodic dynamical systems
In the preceding section, we have met Weyl almost periodic points. In this section, we introduce two special classes of Weyl almost periodic points, namely Bohr almost periodic points and weakly almost periodic points. This allows us to reanalyze and characterize weakly almost periodic dynamical system and Bohr almost periodic dynamical system via the new approach in this paper. Specifically, the main result of this section shows that a (transitive) dynamical system is weakly almost periodic (Bohr almost periodic) if and only if every of its points is weakly almost periodic (Bohr almost periodic). We refer to [Reference Lenz and Strungaru33] for a recent discussion of Bohr and weakly almost periodic systems including relevance, background and further references.
Let G be a
![]() $\sigma $
-compact locally compact abelian group and denote the set of uniformly continuous and bounded functions on G by
$\sigma $
-compact locally compact abelian group and denote the set of uniformly continuous and bounded functions on G by
![]() $C_u (G)$
. This space is a Banach space when equipped with the supremum norm
$C_u (G)$
. This space is a Banach space when equipped with the supremum norm
![]() $\|\cdot \|_\infty $
. An
$\|\cdot \|_\infty $
. An
![]() $f\in C_u (G)$
is called weakly almost periodic if the set
$f\in C_u (G)$
is called weakly almost periodic if the set
![]() $\{f(\cdot -t) : t\in G\}$
is relatively compact in
$\{f(\cdot -t) : t\in G\}$
is relatively compact in
![]() $C_u (G)$
with respect to the weak topology of the Banach space
$C_u (G)$
with respect to the weak topology of the Banach space
![]() $(C_u (G),\|\cdot \|_\infty )$
. Clearly, any Bohr almost periodic
$(C_u (G),\|\cdot \|_\infty )$
. Clearly, any Bohr almost periodic
![]() $f\in C_u (G)$
is weakly almost periodic (as Bohr almost periodicity means, by definition, that the set
$f\in C_u (G)$
is weakly almost periodic (as Bohr almost periodicity means, by definition, that the set
![]() $\{f(\cdot -t) : t\in G\}$
is relatively compact in the original topology). In fact, a main result on weakly almost periodic functions (see, e.g., [Reference Akin and Glasner1] or [Reference Ellis and Nerurkar13, Reference Lenz and Strungaru33]) gives that any weakly almost periodic f can be (uniquely) decomposed into
$\{f(\cdot -t) : t\in G\}$
is relatively compact in the original topology). In fact, a main result on weakly almost periodic functions (see, e.g., [Reference Akin and Glasner1] or [Reference Ellis and Nerurkar13, Reference Lenz and Strungaru33]) gives that any weakly almost periodic f can be (uniquely) decomposed into
![]() $f = g + h$
with
$f = g + h$
with
![]() $g\in C_u (G) $
Bohr almost periodic and
$g\in C_u (G) $
Bohr almost periodic and
![]() $h\in C_u (G)$
satisfying
$h\in C_u (G)$
satisfying
 $$ \begin{align*} \lim_{n\to\infty} \sup_{s\in G} \frac{1}{|B_n|} \int_{B_n} |h(s + t) |\,d t = 0 \end{align*} $$
$$ \begin{align*} \lim_{n\to\infty} \sup_{s\in G} \frac{1}{|B_n|} \int_{B_n} |h(s + t) |\,d t = 0 \end{align*} $$
for any F ølner sequence
![]() $(B_n)$
. The existence of this decomposition is [Reference Moody, Strungaru, Baake and Grimm35, Theorem 4.7.11], whereas the uniqueness follows immediately from [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.6.8].
$(B_n)$
. The existence of this decomposition is [Reference Moody, Strungaru, Baake and Grimm35, Theorem 4.7.11], whereas the uniqueness follows immediately from [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.6.8].
When combined with
![]() $(\heartsuit )$
in Appendix A this easily gives that any weakly almost periodic function is Weyl almost periodic.
$(\heartsuit )$
in Appendix A this easily gives that any weakly almost periodic function is Weyl almost periodic.
Definition 6.1. (Weakly and Bohr almost periodic points)
Let
![]() $(X,G)$
be a dynamical system.
$(X,G)$
be a dynamical system.
-
(a) A point
 $x\in X$
is called weakly almost periodic if
$x\in X$
is called weakly almost periodic if
 $\mathcal {A}_x$
consists only of weakly almost periodic functions.
$\mathcal {A}_x$
consists only of weakly almost periodic functions. -
(b) A point
 $x\in X$
is called Bohr almost periodic if
$x\in X$
is called Bohr almost periodic if
 $\mathcal {A}_x$
consists only of Bohr almost periodic functions.
$\mathcal {A}_x$
consists only of Bohr almost periodic functions.
Remark. By the discussion preceding the definition, any Bohr almost periodic point is weakly almost periodic and any weakly almost periodic point is Weyl almost periodic.
In the subsequent discussion, the weakly almost periodic case and the Bohr almost periodic case can be mostly treated in parallel. To facilitate the reading, we then give statements for the weakly almost periodic case and mention the Bohr almost periodic case in brackets only.
With essentially the same proof as Lemma 3.7, we obtain the following statement.
Lemma 6.2. Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $x \in X$
be given. Then, the following assertions are equivalent.
$x \in X$
be given. Then, the following assertions are equivalent.
-
(i) The point x is weakly (Bohr) almost periodic.
-
(ii) The weakly (Bohr) almost periodic functions in
 $\mathcal {A}_x$
are dense in
$\mathcal {A}_x$
are dense in
 $(\mathcal {A}_x, \| \cdot \|_\infty )$
.
$(\mathcal {A}_x, \| \cdot \|_\infty )$
. -
(iii) The set
 $\{ f \in C(X): f_x \mbox { is weakly (Bohr) almost periodic } \}$
separates the points of X.
$\{ f \in C(X): f_x \mbox { is weakly (Bohr) almost periodic } \}$
separates the points of X. -
(iv) For any
 $s\in G$
the function
$s\in G$
the function
 $d^{(s)}_x$
is weakly (Bohr) almost periodic, where
$d^{(s)}_x$
is weakly (Bohr) almost periodic, where
 $d^{(s)} \in C(X)$
is defined via
$d^{(s)} \in C(X)$
is defined via
 $d^{(s)}(y) : =d(sx,y)$
.
$d^{(s)}(y) : =d(sx,y)$
.
Whenever
![]() $(X,G)$
is a dynamical system, any
$(X,G)$
is a dynamical system, any
![]() $f\in C(X)$
gives rise to a function on the product
$f\in C(X)$
gives rise to a function on the product
![]() $G\times X$
, namely
$G\times X$
, namely
Roughly speaking one can say that the preceding discussion was concerned with almost periodicity properties of the functions
![]() $f_x = P_f (\cdot ,x)$
for
$f_x = P_f (\cdot ,x)$
for
![]() $x\in X$
. It is natural to consider almost periodicity properties of restrictions of the
$x\in X$
. It is natural to consider almost periodicity properties of restrictions of the
![]() $P_f$
to X as well for fixed
$P_f$
to X as well for fixed
![]() $t\in G$
. This leads to the notion of weakly (Bohr) almost periodic dynamical system. For
$t\in G$
. This leads to the notion of weakly (Bohr) almost periodic dynamical system. For
![]() $f\in C(X)$
and
$f\in C(X)$
and
![]() $t\in G$
, we define
$t\in G$
, we define
Definition 6.3. (Weakly and Bohr almost periodic dynamical systems)
The dynamical system
![]() $(X, G)$
is called weakly almost periodic and Bohr almost periodic (in some papers this is called an almost periodic dynamical system or strongly almost periodic dynamical system) if for any
$(X, G)$
is called weakly almost periodic and Bohr almost periodic (in some papers this is called an almost periodic dynamical system or strongly almost periodic dynamical system) if for any
![]() $f\in C(X)$
the family
$f\in C(X)$
the family
![]() $\{f_t : t\in G\}$
has compact closure in the weak topology and the Banach space topology of
$\{f_t : t\in G\}$
has compact closure in the weak topology and the Banach space topology of
![]() $(C(X),\|\cdot \|_\infty )$
, respectively.
$(C(X),\|\cdot \|_\infty )$
, respectively.
The next lemma relates weakly (Bohr) almost periodic dynamical systems to weakly (Bohr) almost periodic points.
Lemma 6.4. Let
![]() $(X,G)$
be a dynamical system.
$(X,G)$
be a dynamical system.
-
(a) If
 $(X,G)$
is weakly (Bohr) almost periodic, then every
$(X,G)$
is weakly (Bohr) almost periodic, then every
 $x \in X$
is a weakly (Bohr) almost periodic.
$x \in X$
is a weakly (Bohr) almost periodic. -
(b) If
 $x \in X$
is transitive and weakly (Bohr) almost periodic, then
$x \in X$
is transitive and weakly (Bohr) almost periodic, then
 $(X,G)$
is a weakly (Bohr) almost periodic dynamical system.
$(X,G)$
is a weakly (Bohr) almost periodic dynamical system.
Proof. Fix an arbitrary
![]() $x \in X$
. Define
$x \in X$
. Define
![]() $F: C(X) \to C_u(G)$
via
$F: C(X) \to C_u(G)$
via
-
(a) It is easy to see that F is well defined and
 $\| F \| \leq 1$
. It follows that F is continuous and, hence, also weakly continuous [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.4.2]. Therefore, the image of a compact (respectively, weak compact) set is compact (respectively, weak compact). As F commutes with the group action, the claim follows.
$\| F \| \leq 1$
. It follows that F is continuous and, hence, also weakly continuous [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.4.2]. Therefore, the image of a compact (respectively, weak compact) set is compact (respectively, weak compact). As F commutes with the group action, the claim follows. -
(b) We know that F is continuous. Moreover, because x has dense orbit, it follows immediately that for all
 $f \in C(X)$
we have Therefore, F is an isometry and, hence, it induces an isomorphic isometry
$f \in C(X)$
we have Therefore, F is an isometry and, hence, it induces an isomorphic isometry $$ \begin{align*} \| F(f) \|_\infty = \| f \|_\infty. \end{align*} $$
$$ \begin{align*} \| F(f) \|_\infty = \| f \|_\infty. \end{align*} $$
 $F: C(X) \to \mbox {Im}(F)$
. In particular,
$F: C(X) \to \mbox {Im}(F)$
. In particular,
 $\mbox {Im}(F)$
is closed in
$\mbox {Im}(F)$
is closed in
 $C_u(G)$
and the mapping is a continuous operator and, hence, is also weakly continuous [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.4.2]. Therefore,
$C_u(G)$
and the mapping is a continuous operator and, hence, is also weakly continuous [Reference Moody, Strungaru, Baake and Grimm35, Lemma 4.4.2]. Therefore, $$ \begin{align*} F^{-1} : \mbox{Im}(F) \to C(X) , \end{align*} $$
$$ \begin{align*} F^{-1} : \mbox{Im}(F) \to C(X) , \end{align*} $$
 $F^{-1}$
maps compact and weakly compact sets into compact and weakly compact sets, respectively. This easily gives the desired statement.
$F^{-1}$
maps compact and weakly compact sets into compact and weakly compact sets, respectively. This easily gives the desired statement.
We obtain the following immediate consequence of the preceding lemma.
Theorem 6.5. Let
![]() $(X,G)$
be a dynamical system with transitive
$(X,G)$
be a dynamical system with transitive
![]() $p \in X$
. Then, the following assertions are equivalent.
$p \in X$
. Then, the following assertions are equivalent.
-
(i)
 $(X,G)$
is weakly almost periodic.
$(X,G)$
is weakly almost periodic. -
(ii) Every
 $x \in X$
is weakly almost periodic.
$x \in X$
is weakly almost periodic. -
(iii) The point
 $p\in X$
is weakly almost periodic.
$p\in X$
is weakly almost periodic.
We also note the following consequence of the theorem.
Corollary 6.6. Let
![]() $(X,G)$
be a dynamical system with transitive
$(X,G)$
be a dynamical system with transitive
![]() $p\in X$
. For
$p\in X$
. For
![]() $s,t \in G$
define
$s,t \in G$
define
![]() $g_{s,t}: X \to \mathbb {C}$
via
$g_{s,t}: X \to \mathbb {C}$
via
Then,
![]() $p\in X$
is weakly almost periodic if and only if for each
$p\in X$
is weakly almost periodic if and only if for each
![]() $s \in G$
the set
$s \in G$
the set
![]() $\{ g_{s,t} : t \in G \}$
has compact closure in the weak topology of
$\{ g_{s,t} : t \in G \}$
has compact closure in the weak topology of
![]() $(C(X),\|\cdot \|_\infty )$
.
$(C(X),\|\cdot \|_\infty )$
.
Proof. Indeed, the only if part of the statement is immediate from the definition of weak almost periodicity and the preceding theorem. To show the if part, we denote (in line with [Reference Lenz and Strungaru33])
Then, by [Reference Lenz and Strungaru33, Propositions 3.3, 3.4]
![]() $\operatorname {WAP}(X)$
is a closed algebra of
$\operatorname {WAP}(X)$
is a closed algebra of
![]() $(C(X), \| \cdot \|_\infty )$
, which contains the constant function 1. Moreover, we have
$(C(X), \| \cdot \|_\infty )$
, which contains the constant function 1. Moreover, we have
![]() $g_{t,1} \in \operatorname {WAP}(X)$
for all
$g_{t,1} \in \operatorname {WAP}(X)$
for all
![]() $t\in G$
. We next show that the functions
$t\in G$
. We next show that the functions
![]() $g_{t,1}$
separate the points of X. Let
$g_{t,1}$
separate the points of X. Let
![]() $x \neq y \in X$
be arbitrary, and let
$x \neq y \in X$
be arbitrary, and let
![]() $r=d(x,y)$
.
$r=d(x,y)$
.
As p is a transitive point, there exists some
![]() $t \in G$
such that
$t \in G$
such that
![]() $d(tp,x) < {r}/{3}$
. Then,
$d(tp,x) < {r}/{3}$
. Then,
This shows that
![]() $g_{t,1}(x) {\kern-1.3pt}\neq{\kern-1.3pt} g_{t,1}(y)$
. Therefore,
$g_{t,1}(x) {\kern-1.3pt}\neq{\kern-1.3pt} g_{t,1}(y)$
. Therefore,
![]() $\operatorname {WAP}(X)$
is a closed algebra of
$\operatorname {WAP}(X)$
is a closed algebra of
![]() $(C(X), \|{\kern-1pt} \cdot{\kern-1pt} \|_\infty )$
which is separating the points and, hence, by the Stone–Weierstraß theorem,
$(C(X), \|{\kern-1pt} \cdot{\kern-1pt} \|_\infty )$
which is separating the points and, hence, by the Stone–Weierstraß theorem,
![]() $\operatorname {WAP}(X)=C(X)$
. This gives the desired statement.
$\operatorname {WAP}(X)=C(X)$
. This gives the desired statement.
The preceding theorem allows us to recapture a main result of [Reference Lenz and Strungaru33] (compare with [Reference Garcia-Ramos and Marcus19, Corollary 2.18]).
Corollary 6.7. Let
![]() $(X,G)$
be a transitive weakly almost periodic dynamical system. Then,
$(X,G)$
be a transitive weakly almost periodic dynamical system. Then,
![]() $(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
$(X,G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
Proof. Let p be a transitive point. Then, by Theorem 6.5, p is weakly almost periodic. Hence, p is Weyl almost periodic as well and the claim follows from Theorem 5.5.
As should be clear from the preceding discussion, the analog of Theorem 6.5 with ‘weakly almost periodic’ replaced by ‘Bohr almost periodic’ holds as well (and, similarly, for Corollary 6.6). In fact, a somewhat stronger statement is true for Bohr almost periodic points. To state this properly, we introduce the following notation when dealing with an dynamical system
![]() $(X,G)$
with metric d. For
$(X,G)$
with metric d. For
![]() $f\in C(X)$
we consider the mapping
$f\in C(X)$
we consider the mapping
and, when an
![]() $x\in X$
is fixed, we set
$x\in X$
is fixed, we set
where the closure is taken in
![]() $C_u (G)$
with the (usual) supremum norm. We also define
$C_u (G)$
with the (usual) supremum norm. We also define
Clearly,
![]() $\overline {d}$
is a metric.
$\overline {d}$
is a metric.
Theorem 6.8. Let
![]() $(X,G)$
be a dynamical system. For
$(X,G)$
be a dynamical system. For
![]() $x\in X$
the following assertions are equivalent.
$x\in X$
the following assertions are equivalent.
-
(i) The element
 $x\in X$
is Bohr almost periodic.
$x\in X$
is Bohr almost periodic. -
(ii) For any
 $f\in C(X)$
, the map
$f\in C(X)$
, the map
 $\pi _f : \overline {Gx} \longrightarrow C_u (G)$
,
$\pi _f : \overline {Gx} \longrightarrow C_u (G)$
,
 $y\mapsto f_y$
, is continuous with range given by
$y\mapsto f_y$
, is continuous with range given by
 $Y(f,x)$
.
$Y(f,x)$
. -
(iii) There exists a G-invariant metric on
 $\overline {Gx}$
generating the topology.
$\overline {Gx}$
generating the topology. -
(iv) The function
 $\overline {d}$
is continuous on
$\overline {d}$
is continuous on
 $\overline {Gx}$
.
$\overline {Gx}$
. -
(v) The orbit closure
 $\overline {Gx}$
admits a structure of a locally compact group such that
$\overline {Gx}$
admits a structure of a locally compact group such that
 $G\longrightarrow \overline {Gx}$
,
$G\longrightarrow \overline {Gx}$
,
 $t\mapsto t x$
, becomes a continuous group homomorphism.
$t\mapsto t x$
, becomes a continuous group homomorphism.
In particular, the orbit closure of any Bohr almost periodic point is minimal.
Proof. (i)
![]() $\Longrightarrow $
(ii): Clearly,
$\Longrightarrow $
(ii): Clearly,
![]() $\pi _f (tx) = f_{tx} = f_x (\cdot +t)$
for any
$\pi _f (tx) = f_{tx} = f_x (\cdot +t)$
for any
![]() $t\in G$
. Thus, it suffices to show that
$t\in G$
. Thus, it suffices to show that
![]() $f_y$
belongs indeed to
$f_y$
belongs indeed to
![]() $Y(f,x)$
for any
$Y(f,x)$
for any
![]() $y\in \overline {Gx}$
and
$y\in \overline {Gx}$
and
![]() $\pi _f$
is continuous on
$\pi _f$
is continuous on
![]() $Y(f,x)$
. It is enough to show that
$Y(f,x)$
. It is enough to show that
![]() $\pi _f(y_n)$
converges to
$\pi _f(y_n)$
converges to
![]() $\pi _f (y)$
whenever
$\pi _f (y)$
whenever
![]() $(y_n)$
is a sequence in
$(y_n)$
is a sequence in
![]() $\overline {Gx}$
converging to
$\overline {Gx}$
converging to
![]() $y\in \overline {Gx}$
such that
$y\in \overline {Gx}$
such that
![]() $\pi _f (y_n)$
belongs to
$\pi _f (y_n)$
belongs to
![]() $Y(f,x)$
. Now, it is not hard to see that the functions
$Y(f,x)$
. Now, it is not hard to see that the functions
![]() $\pi _f (y_n)$
converge pointwise to
$\pi _f (y_n)$
converge pointwise to
![]() $\pi _f (y)$
. Moreover, by assertion (i), the set
$\pi _f (y)$
. Moreover, by assertion (i), the set
![]() $Y(f,x)$
is compact and, hence,
$Y(f,x)$
is compact and, hence,
![]() $\pi _f(y_n)$
has a uniform convergent subsequence. Now, any such subsequence must converge to
$\pi _f(y_n)$
has a uniform convergent subsequence. Now, any such subsequence must converge to
![]() $\pi _f (y)$
(as uniform convergence implies pointwise convergence). This gives the desired convergence statement.
$\pi _f (y)$
(as uniform convergence implies pointwise convergence). This gives the desired convergence statement.
(ii)
![]() $\Longrightarrow $
(iii): By assertion (ii), the map
$\Longrightarrow $
(iii): By assertion (ii), the map
![]() $\overline {d}_f$
with
$\overline {d}_f$
with
![]() $\overline {d}_f (y,z) := \|\pi _f (y) - \pi _f (z)\|_\infty $
is a continuous pseudometric on
$\overline {d}_f (y,z) := \|\pi _f (y) - \pi _f (z)\|_\infty $
is a continuous pseudometric on
![]() $\overline {Gx}$
. It is clearly invariant. Now, choose a countable dense subset
$\overline {Gx}$
. It is clearly invariant. Now, choose a countable dense subset
![]() $D\subset C(X)$
separating the points of
$D\subset C(X)$
separating the points of
![]() $\overline {Gx}$
. Assume without loss of generality that any element of D is normalized, and choose for any
$\overline {Gx}$
. Assume without loss of generality that any element of D is normalized, and choose for any
![]() $f{\kern-1.3pt}\in{\kern-1.3pt} D$
a
$f{\kern-1.3pt}\in{\kern-1.3pt} D$
a
![]() $c_f{\kern-1.3pt}>{\kern-1.3pt}0$
with
$c_f{\kern-1.3pt}>{\kern-1.3pt}0$
with
![]() $\sum _{f\in D} c_f {\kern-1.3pt}<{\kern-1.3pt}\infty $
. Then,
$\sum _{f\in D} c_f {\kern-1.3pt}<{\kern-1.3pt}\infty $
. Then,
![]() $\sum _{f\in D} c_f \overline {d}_f$
is a continuous invariant metric on
$\sum _{f\in D} c_f \overline {d}_f$
is a continuous invariant metric on
![]() $\overline {Gx}$
. As
$\overline {Gx}$
. As
![]() $\overline {Gx}$
is compact any continuous metric determines its topology.
$\overline {Gx}$
is compact any continuous metric determines its topology.
(iii)
![]() $\Longrightarrow $
(iv): Let
$\Longrightarrow $
(iv): Let
![]() $\overline {d}'$
be a continuous invariant metric on
$\overline {d}'$
be a continuous invariant metric on
![]() $\overline {Gx}$
. Let
$\overline {Gx}$
. Let
![]() $\varepsilon>0$
be arbitrary. As
$\varepsilon>0$
be arbitrary. As
![]() $\overline {d}'$
is a continuous metric on
$\overline {d}'$
is a continuous metric on
![]() $\overline {Gx}$
there exists a
$\overline {Gx}$
there exists a
![]() $\delta>0$
with
$\delta>0$
with
![]() $d(y_1,y_2)\leq \varepsilon $
for
$d(y_1,y_2)\leq \varepsilon $
for
![]() $y_1,y_2\in \overline {Gx}$
whenever
$y_1,y_2\in \overline {Gx}$
whenever
![]() $\overline {d}'(y_1,y_2)\leq \delta $
. As
$\overline {d}'(y_1,y_2)\leq \delta $
. As
![]() $\overline {d}'$
is invariant, we obtain then
$\overline {d}'$
is invariant, we obtain then
![]() $d(t y_1, t y_2)\leq \varepsilon $
for all
$d(t y_1, t y_2)\leq \varepsilon $
for all
![]() $t\in G$
and, hence,
$t\in G$
and, hence,
![]() $\overline {d}(y_1,y_2)\leq \varepsilon $
whenever
$\overline {d}(y_1,y_2)\leq \varepsilon $
whenever
![]() $\overline {d}'(y_1,y_2)\leq \delta $
for
$\overline {d}'(y_1,y_2)\leq \delta $
for
![]() $y_1,y_2\in \overline {Gx}$
. This is the desired statement.
$y_1,y_2\in \overline {Gx}$
. This is the desired statement.
(iv)
![]() $\Longrightarrow $
(v): Using the invariant metric
$\Longrightarrow $
(v): Using the invariant metric
![]() $\overline {d}$
it is not hard to see that there is a group structure on
$\overline {d}$
it is not hard to see that there is a group structure on
![]() $\overline {Gx}$
with
$\overline {Gx}$
with
![]() $tx + sx = (t+s)x$
. Here, we show only that this is well defined. The remaining statements then follow easily. Assume
$tx + sx = (t+s)x$
. Here, we show only that this is well defined. The remaining statements then follow easily. Assume
![]() $tx = t'x$
and
$tx = t'x$
and
![]() $sx = s'x$
. Then triangle inequality and invariance of the metric gives
$sx = s'x$
. Then triangle inequality and invariance of the metric gives
 $$ \begin{align*}\overline{d}((t+s)x,(t' + s')x)&\leq \overline{d}((t+s)x,(t+s')x) +\overline{d}((t+s')x, (t' + s')x)\\ &\leq \overline{d}(sx,s'x) + \overline{d}(tx,t'x) = 0.\end{align*} $$
$$ \begin{align*}\overline{d}((t+s)x,(t' + s')x)&\leq \overline{d}((t+s)x,(t+s')x) +\overline{d}((t+s')x, (t' + s')x)\\ &\leq \overline{d}(sx,s'x) + \overline{d}(tx,t'x) = 0.\end{align*} $$
This shows well definedness.
(v)
![]() $\Longrightarrow $
(i): This is standard. We include some details for convenience of the reader. Let f be a continuous function on X. We have to show that the set
$\Longrightarrow $
(i): This is standard. We include some details for convenience of the reader. Let f be a continuous function on X. We have to show that the set
![]() $S:=\{f_x (t + \cdot ): t\in G\} = \{f_{tx} : t\in G\}$
has compact closure in
$S:=\{f_x (t + \cdot ): t\in G\} = \{f_{tx} : t\in G\}$
has compact closure in
![]() $C_u (G)$
with respect to the supremum norm. From assertion (iv), we easily see that
$C_u (G)$
with respect to the supremum norm. From assertion (iv), we easily see that
![]() $\pi _f : \overline {Gx}\longrightarrow C_u (G), y\mapsto f_y$
, is continuous. Hence,
$\pi _f : \overline {Gx}\longrightarrow C_u (G), y\mapsto f_y$
, is continuous. Hence,
![]() $\pi _f (\overline {Gx})$
is compact and, as it clearly contains S, the desired statement follows.
$\pi _f (\overline {Gx})$
is compact and, as it clearly contains S, the desired statement follows.
The minimality statement follows directly from assertion (iii).
The preceding result shows that Bohr almost periodic points give rise to minimal orbit closures. In fact, within the weakly almost periodic points one can even characterize the Bohr almost periodic points by minimality of their orbit closures.
Proposition 6.9. Let
![]() $(X,G)$
be a dynamical system and let
$(X,G)$
be a dynamical system and let
![]() $x\in X$
be weakly almost periodic. Then, x is Bohr almost periodic if and only if its orbit closure
$x\in X$
be weakly almost periodic. Then, x is Bohr almost periodic if and only if its orbit closure
![]() $\overline {Gx}$
is minimal.
$\overline {Gx}$
is minimal.
Proof. We have just seen in Theorem 6.8 that the orbit closure of a Bohr almost periodic point is minimal. Thus, consider now a weakly almost periodic point
![]() $x\in X$
with minimal orbit closure
$x\in X$
with minimal orbit closure
![]() $\overline {Gx}$
. Then, clearly
$\overline {Gx}$
. Then, clearly
![]() $(\overline {Gx},G)$
is weakly almost periodic by Lemma 6.4(b) and it is minimal (by assumption). Now, as is well known (see, e.g., [Reference Lenz and Strungaru33]) any minimal component of a weakly almost periodic system is Bohr almost periodic. Now, the desired claim follows from Lemma 6.4(a).
$(\overline {Gx},G)$
is weakly almost periodic by Lemma 6.4(b) and it is minimal (by assumption). Now, as is well known (see, e.g., [Reference Lenz and Strungaru33]) any minimal component of a weakly almost periodic system is Bohr almost periodic. Now, the desired claim follows from Lemma 6.4(a).
Remark. We note that a Bohr almost periodic dynamical system does not need to be minimal as can easily be seen by considering the ‘disjoint union’ of two Bohr almost periodic systems.
It is possible to characterize Bohr almost periodic points by almost periodicity properties of the metric
![]() $\overline {d}$
.
$\overline {d}$
.
Theorem 6.10. Let
![]() $(X,G)$
be a dynamical system with metric d. Then the following assertions are equivalent for a point
$(X,G)$
be a dynamical system with metric d. Then the following assertions are equivalent for a point
![]() $p\in X$
.
$p\in X$
.
-
(i) The point p is Bohr almost periodic.
-
(ii) The function
 $G\mapsto [0,\infty )$
,
$G\mapsto [0,\infty )$
,
 $t\mapsto \overline {d}(p,tp)$
, is Bohr almost periodic.
$t\mapsto \overline {d}(p,tp)$
, is Bohr almost periodic.
Proof. We show that (i) implies (ii): by assertion (i) and Theorem 6.8, the orbit closure of p is minimal and the function
![]() $\overline {d}$
is a continuous metric on
$\overline {d}$
is a continuous metric on
![]() $\overline {Gp}$
. Let
$\overline {Gp}$
. Let
![]() $\varepsilon>0$
be given. As
$\varepsilon>0$
be given. As
![]() $\overline {d}$
is continuous and every Bohr almost periodic point has a minimal orbit, there exists a relatively dense set
$\overline {d}$
is continuous and every Bohr almost periodic point has a minimal orbit, there exists a relatively dense set
![]() $R\subset G$
with
$R\subset G$
with
![]() $\overline {d}(sp,p)< \varepsilon $
for all
$\overline {d}(sp,p)< \varepsilon $
for all
![]() $s\in R$
. As
$s\in R$
. As
![]() $\overline {d}$
is invariant, this gives
$\overline {d}$
is invariant, this gives
for all
![]() $t\in G$
and
$t\in G$
and
![]() $s\in R$
. As
$s\in R$
. As
![]() $\varepsilon>0$
was arbitrary this gives assertion (ii).
$\varepsilon>0$
was arbitrary this gives assertion (ii).
We now show that assertion (ii) implies that p is Bohr almost periodic: it is not hard to see that assertion (ii) implies that
![]() $t \mapsto d(sp,(t+s),p)$
is Bohr almost periodic for any
$t \mapsto d(sp,(t+s),p)$
is Bohr almost periodic for any
![]() $s\in G$
. This easily implies that Lemma 6.2(iv) holds and assertion (i) follows from that lemma.
$s\in G$
. This easily implies that Lemma 6.2(iv) holds and assertion (i) follows from that lemma.
7 Application to measure dynamical systems
In this section, we use our results to shed light on recent investigations of aperiodic order. A fundamental issue in the study of aperiodic order is pure point diffraction; see, e.g., [Reference Baake and Lenz4] for a recent survey. Indeed, understanding of pure point diffraction has been a driving force in the field; see, e.g., the survey article [Reference Lagarias, Baake and Moody25]. Recently, a complete understanding of pure point diffraction via mean almost periodicity has been provided in [Reference Lenz, Spindeler and Strungaru31]. That article mostly deals with single measures. However, it also includes results on pure point spectrum of certain dynamical systems, namely measure dynamical systems. Here, we discuss how our results allow one to provide a different approach to these results.
We start with a discussion of TMDSs. Such dynamical systems were brought forward in [Reference Baake and Lenz3] to provide a systematic framework to study aperiodic order. In our exposition we follow [Reference Baake and Lenz3] to which we refer for further details, proofs and references.
We denote by
![]() $C_c (G)$
the vector space of continuous complex-valued functions on G with compact support. This space is equipped with the inductive limit topology of the injections
$C_c (G)$
the vector space of continuous complex-valued functions on G with compact support. This space is equipped with the inductive limit topology of the injections
for
![]() $K\subset G$
compact. Here,
$K\subset G$
compact. Here,
![]() $C_K (G)$
denotes the subspace of
$C_K (G)$
denotes the subspace of
![]() $C_c (G)$
consisting of functions with support in K. The measures on G are the elements of the dual space of
$C_c (G)$
consisting of functions with support in K. The measures on G are the elements of the dual space of
![]() $C_c (G)$
. The total variation
$C_c (G)$
. The total variation
![]() $|\mu |$
of a measure
$|\mu |$
of a measure
![]() $\mu $
is the smallest positive measure with
$\mu $
is the smallest positive measure with
for all
![]() $\varphi \in C_c (G)$
with
$\varphi \in C_c (G)$
with
![]() $\varphi \geq 0$
. A measure
$\varphi \geq 0$
. A measure
![]() $\mu $
on G is called translation bounded if its total variation
$\mu $
on G is called translation bounded if its total variation
![]() $|\mu |$
satisfies
$|\mu |$
satisfies
for one (all) relatively compact open U in G. We denote that set of all translation bounded measures by
![]() $M^\infty (G)$
and equip it with the vague topology. Then, G admits a natural action on
$M^\infty (G)$
and equip it with the vague topology. Then, G admits a natural action on
![]() $M^\infty (G)$
by translations. More specifically, for
$M^\infty (G)$
by translations. More specifically, for
![]() $t\in G$
and
$t\in G$
and
![]() $\mu \in M^\infty (G)$
the measure
$\mu \in M^\infty (G)$
the measure
![]() $t\mu $
is defined by
$t\mu $
is defined by
for all
![]() $\varphi \in C_c (G)$
.
$\varphi \in C_c (G)$
.
A subset
![]() $\varOmega \subset M^\infty (G)$
which is invariant under the translation action is compact if and only if it is vaguely closed and there exists a constant C such that [Reference Spindeler and Strungaru39, Theorem A.8]
$\varOmega \subset M^\infty (G)$
which is invariant under the translation action is compact if and only if it is vaguely closed and there exists a constant C such that [Reference Spindeler and Strungaru39, Theorem A.8]
Whenever
![]() $\varOmega $
is a compact subset of
$\varOmega $
is a compact subset of
![]() $M^\infty (G)$
, which is invariant under the translation action to and m is an invariant probability measure on X, we call
$M^\infty (G)$
, which is invariant under the translation action to and m is an invariant probability measure on X, we call
![]() $(X,G,m)$
a dynamical system of translation bounded measures or just TMDS for short. If G is second countable than any TMDS is metrizable. Hence, the theory developed above applies to TMDS whenever G is second countable. Consider now an arbitrary TMDS
$(X,G,m)$
a dynamical system of translation bounded measures or just TMDS for short. If G is second countable than any TMDS is metrizable. Hence, the theory developed above applies to TMDS whenever G is second countable. Consider now an arbitrary TMDS
![]() $(\varOmega ,G,m)$
and define for any
$(\varOmega ,G,m)$
and define for any
![]() $\varphi \in C_c (G)$
the function
$\varphi \in C_c (G)$
the function
Then,
![]() $N_\varphi $
belongs to
$N_\varphi $
belongs to
![]() $C(\varOmega )$
. In addition, there exists a unique translation bounded measure
$C(\varOmega )$
. In addition, there exists a unique translation bounded measure
![]() $\gamma = \gamma ^m$
on
$\gamma = \gamma ^m$
on
![]() $(X,G,m)$
with
$(X,G,m)$
with
for all
![]() $\varphi ,\psi \in C_c (G)$
and all
$\varphi ,\psi \in C_c (G)$
and all
![]() $t\in G$
. (Note that [Reference Baake and Lenz3] uses a different sign in the definition of
$t\in G$
. (Note that [Reference Baake and Lenz3] uses a different sign in the definition of
![]() ${N}$
(called f there) as well as has the inner product linear in the second argument. This results in a different display of the formula for
${N}$
(called f there) as well as has the inner product linear in the second argument. This results in a different display of the formula for
![]() $\gamma $
, namely
$\gamma $
, namely
![]() $(\gamma \ast \widetilde {\varphi }\ast \psi )(0) = \langle f_\varphi , f_\psi \rangle $
.) The measure
$(\gamma \ast \widetilde {\varphi }\ast \psi )(0) = \langle f_\varphi , f_\psi \rangle $
.) The measure
![]() $\gamma $
is called the autocorrelation of the TMDS. This measure allows for a Fourier transform
$\gamma $
is called the autocorrelation of the TMDS. This measure allows for a Fourier transform
![]() $\widehat {\gamma }$
which is a (positive) measure on
$\widehat {\gamma }$
which is a (positive) measure on
![]() $\widehat {G}$
. It is known as diffraction of the TMDS. Of particular interest in this theory are now those TMDSs whose diffraction is a pure point measure. By a main result of [Reference Baake and Lenz3] (see references there also for earlier results) the diffraction of a TMDS is pure point if and only if the TMDS has pure point spectrum. Thus, for this reason, TMDSs with pure point spectrum are of utmost relevance in the field of aperiodic order. One particular question is the calculation of the atoms of
$\widehat {G}$
. It is known as diffraction of the TMDS. Of particular interest in this theory are now those TMDSs whose diffraction is a pure point measure. By a main result of [Reference Baake and Lenz3] (see references there also for earlier results) the diffraction of a TMDS is pure point if and only if the TMDS has pure point spectrum. Thus, for this reason, TMDSs with pure point spectrum are of utmost relevance in the field of aperiodic order. One particular question is the calculation of the atoms of
![]() $\widehat {\gamma }$
. Here, the basic idea is that
$\widehat {\gamma }$
. Here, the basic idea is that
 $$ \begin{align*} \widehat{\gamma} (\{\xi\}) = \lim_{n \to \infty}\bigg|\frac{1}{|B_n|} \int_{B_n} \xi (t)\,d\omega (t)\bigg|^2 \end{align*} $$
$$ \begin{align*} \widehat{\gamma} (\{\xi\}) = \lim_{n \to \infty}\bigg|\frac{1}{|B_n|} \int_{B_n} \xi (t)\,d\omega (t)\bigg|^2 \end{align*} $$
(with
![]() $(B_n)$
being a Følner sequence). Validity of this formula is often discussed under the heading of the Bombieri–Taylor conjecture.
$(B_n)$
being a Følner sequence). Validity of this formula is often discussed under the heading of the Bombieri–Taylor conjecture.
Having provided the framework of TMDSs, we now discuss how the theory developed in the previous section can be used in the study of aperiodic order.
A translation bounded measure
![]() $\omega $
is called mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, respectively) if for any
$\omega $
is called mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, respectively) if for any
![]() $\varphi \in C_c (G)$
the function
$\varphi \in C_c (G)$
the function
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, respectively).
Proposition 7.1. Let
![]() $(\varOmega ,G,m)$
be a TMDS and let
$(\varOmega ,G,m)$
be a TMDS and let
![]() $(B_n)$
be a Følner sequence. Then, for
$(B_n)$
be a Følner sequence. Then, for
![]() $\omega \in \varOmega $
the following assertions are equivalent.
$\omega \in \varOmega $
the following assertions are equivalent.
-
(i) The measure
 $\omega $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic).
$\omega $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic). -
(ii) The function
 $t\mapsto N_\varphi (t\omega ) $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic) for any
$t\mapsto N_\varphi (t\omega ) $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic) for any
 $\varphi \in C_c (G)$
.
$\varphi \in C_c (G)$
. -
(iii) The point
 $\omega \in \Omega $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic).
$\omega \in \Omega $
is mean almost periodic (Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic).
Proof. We only discuss mean almost periodicity. The remaining statements follow analogously.
(i)
![]() $\Longleftrightarrow $
(ii): A short computation shows
$\Longleftrightarrow $
(ii): A short computation shows
where
![]() $\widetilde {\varphi } : G\longrightarrow \mathbb {C}$
,
$\widetilde {\varphi } : G\longrightarrow \mathbb {C}$
,
![]() $t\mapsto \overline {\varphi }(-t)$
. This gives that
$t\mapsto \overline {\varphi }(-t)$
. This gives that
![]() $\omega $
is mean almost periodic if and only if
$\omega $
is mean almost periodic if and only if
![]() $t\mapsto N_\varphi (t\omega )$
,
$t\mapsto N_\varphi (t\omega )$
,
![]() $\varphi \in C_c (G)$
, is mean almost periodic and the equivalence between assertions (i) and (ii) follows.
$\varphi \in C_c (G)$
, is mean almost periodic and the equivalence between assertions (i) and (ii) follows.
(iii)
![]() $\Longrightarrow $
(ii): This follows easily as any
$\Longrightarrow $
(ii): This follows easily as any
![]() $N_\varphi $
,
$N_\varphi $
,
![]() $\varphi \in C_c (G)$
, is a continuous function on
$\varphi \in C_c (G)$
, is a continuous function on
![]() $\Omega $
.
$\Omega $
.
(ii)
![]() $\Longrightarrow $
(iii): It is not hard to see that the set of
$\Longrightarrow $
(iii): It is not hard to see that the set of
![]() $N_\varphi $
,
$N_\varphi $
,
![]() $\varphi \in C_c (G)$
, separates the points of
$\varphi \in C_c (G)$
, separates the points of
![]() $\Omega $
and is closed under complex conjugation. Hence, the algebra generated by the
$\Omega $
and is closed under complex conjugation. Hence, the algebra generated by the
![]() $N_\varphi $
is dense in the continuous functions on
$N_\varphi $
is dense in the continuous functions on
![]() $\Omega $
with respect to the supremum norm (see, e.g., [Reference Baake and Lenz4] for further discussion of this type of argument). This gives that assertion (ii) implies assertion (iii).
$\Omega $
with respect to the supremum norm (see, e.g., [Reference Baake and Lenz4] for further discussion of this type of argument). This gives that assertion (ii) implies assertion (iii).
When dealing with TMDS
![]() $(\Omega ,G,m)$
we can now use the previous proposition to replace the assumption that
$(\Omega ,G,m)$
we can now use the previous proposition to replace the assumption that
![]() $\omega \in \Omega $
is mean almost periodic as element of the dynamical system
$\omega \in \Omega $
is mean almost periodic as element of the dynamical system
![]() $(\Omega ,G,m)$
by the assumption that
$(\Omega ,G,m)$
by the assumption that
![]() $\omega $
is a mean almost periodic measure (and, similarly, with mean almost periodic replaced by Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic). This allows then for reformulations of our main results. We include the most important consequences next.
$\omega $
is a mean almost periodic measure (and, similarly, with mean almost periodic replaced by Besicovitch almost periodic, Weyl almost periodic, weak almost periodic, Bohr almost periodic). This allows then for reformulations of our main results. We include the most important consequences next.
Theorem 7.2. Let
![]() $(\varOmega ,G,m)$
be an ergodic TMDS. Assume that G is second countable and that
$(\varOmega ,G,m)$
be an ergodic TMDS. Assume that G is second countable and that
![]() $(B_n)$
is a Følner sequence along which Birkhoff’s ergodic theorem holds. Then, the following assertions are equivalent.
$(B_n)$
is a Følner sequence along which Birkhoff’s ergodic theorem holds. Then, the following assertions are equivalent.
-
(i)
 $(\varOmega ,G,m)$
has pure point spectrum.
$(\varOmega ,G,m)$
has pure point spectrum. -
(ii) Almost every
 $\omega \in \varOmega $
is a mean almost periodic measure.
$\omega \in \varOmega $
is a mean almost periodic measure. -
(iii) Almost every
 $\omega \in \varOmega $
is a Besicovitch almost periodic measure.
$\omega \in \varOmega $
is a Besicovitch almost periodic measure.
Moreover, in this case, for each
![]() $\xi \in \widehat {G}$
with
$\xi \in \widehat {G}$
with
![]() $\widehat {\gamma }(\{ \xi \})\neq 0$
, the Fourier–Bohr coefficient
$\widehat {\gamma }(\{ \xi \})\neq 0$
, the Fourier–Bohr coefficient
 $$ \begin{align*} a_{\xi}(\omega)= \lim_n \frac{1}{|B_n|} \int_{B_n} \overline{\xi(t)} \, d \omega(t) \end{align*} $$
$$ \begin{align*} a_{\xi}(\omega)= \lim_n \frac{1}{|B_n|} \int_{B_n} \overline{\xi(t)} \, d \omega(t) \end{align*} $$
exists for m-almost all
![]() $\omega $
and satisfies
$\omega $
and satisfies
Furthermore, there exists a non-trivial eigenfunction
![]() $f_\xi \in L^1(\varOmega , m)$
such that
$f_\xi \in L^1(\varOmega , m)$
such that
![]() $f_\chi (\omega )=a_\chi (\omega )$
for all
$f_\chi (\omega )=a_\chi (\omega )$
for all
![]() $\omega \in \mathrm {Bap} (X,G,m)$
.
$\omega \in \mathrm {Bap} (X,G,m)$
.
Proof. The equivalence follows by combining Theorems 3.8, 4.7 and Proposition 7.1.
Next, let
![]() $\xi \in \widehat {G}$
with
$\xi \in \widehat {G}$
with
![]() $\widehat {\gamma }(\{ \xi \})\neq 0$
and let
$\widehat {\gamma }(\{ \xi \})\neq 0$
and let
![]() $\varphi \in C_c(G)$
be so that
$\varphi \in C_c(G)$
be so that
![]() $\widehat {\varphi }(\xi ) \neq 0$
. Then, by Proposition 4.2 applied to
$\widehat {\varphi }(\xi ) \neq 0$
. Then, by Proposition 4.2 applied to
![]() $N_\varphi $
, the limit
$N_\varphi $
, the limit
 $$ \begin{align*} A((N_\varphi)_\omega\bar{\xi}):= \lim_n \frac{1}{|B_n|} \int_{B_n} \overline{\xi(t)} \varphi*\omega(t) \, d t \end{align*} $$
$$ \begin{align*} A((N_\varphi)_\omega\bar{\xi}):= \lim_n \frac{1}{|B_n|} \int_{B_n} \overline{\xi(t)} \varphi*\omega(t) \, d t \end{align*} $$
exists for m almost all
![]() $\omega \in X$
. By [Reference Lenz, Spindeler and Strungaru31, Corollary 1.1], the Fourier–Bohr coefficients exist for all such
$\omega \in X$
. By [Reference Lenz, Spindeler and Strungaru31, Corollary 1.1], the Fourier–Bohr coefficients exist for all such
![]() $\omega $
and satisfy
$\omega $
and satisfy
Theorem 4.7 the implies the existence of the eigenfunction.
Finally, by [Reference Baake and Lenz4],
![]() $| \widehat {\varphi } |^2 \widehat {\gamma }$
is the spectral measure for
$| \widehat {\varphi } |^2 \widehat {\gamma }$
is the spectral measure for
![]() $N_\varphi \in L^2(X,m)$
. The last claim follows now from Theorem 4.7 and [Reference Lenz27, Theorem 3].
$N_\varphi \in L^2(X,m)$
. The last claim follows now from Theorem 4.7 and [Reference Lenz27, Theorem 3].
By combining Theorem 4.4 with Proposition 7.1 we also immediately obtain the following consequence.
Theorem 7.3. Let
![]() $\omega $
be a Besicovitch almost periodic measure and let
$\omega $
be a Besicovitch almost periodic measure and let
![]() $(B_n)$
be a van Hove sequence along which Birkhoff’s ergodic theorem holds. Then, there exists a (unique) G-invariant ergodic measure m on
$(B_n)$
be a van Hove sequence along which Birkhoff’s ergodic theorem holds. Then, there exists a (unique) G-invariant ergodic measure m on
![]() $\mathbb {X}(\mu )$
such that
$\mathbb {X}(\mu )$
such that
![]() $\mu $
is generic for m.
$\mu $
is generic for m.
Finally, by combining Theorem 5.5 with Proposition 7.1 we also get the following result.
Theorem 7.4. Let
![]() $\omega $
be a translation bounded measure and let
$\omega $
be a translation bounded measure and let
![]() $(B_n)$
be a van Hove sequence along which Birkhoff’s ergodic theorem holds. Then, the following are equivalent.
$(B_n)$
be a van Hove sequence along which Birkhoff’s ergodic theorem holds. Then, the following are equivalent.
-
(i)
 $\mu $
is Weyl almost periodic.
$\mu $
is Weyl almost periodic. -
(ii) Every
 $\omega \in \mathbb {X}(\mu )$
is Weyl almost periodic.
$\omega \in \mathbb {X}(\mu )$
is Weyl almost periodic. -
(iii) The dynamical system
 $(\mathbb {X}(\mu ),G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
$(\mathbb {X}(\mu ),G)$
is uniquely ergodic with pure point spectrum and continuous eigenfunctions.
8 Abstract generalizations
When closing the article, it may be instructive to stop a moment to have a look at the overall theme of this article from a more abstract point of view. The general approach in this article may be described as follows: we consider a dynamical system
![]() $(X,G)$
and say that a point
$(X,G)$
and say that a point
![]() $x\in X$
is
$x\in X$
is
![]() $(*)$
almost periodic if
$(*)$
almost periodic if
![]() $\mathcal {A}_x$
consists of
$\mathcal {A}_x$
consists of
![]() $(*)$
almost periodic functions only. Then, the preceding sections have been devoted to a thorough study of consequences of existence of
$(*)$
almost periodic functions only. Then, the preceding sections have been devoted to a thorough study of consequences of existence of
![]() $(*)$
almost periodic points for
$(*)$
almost periodic points for
![]() $(*)$
being replaced by Bohr, weak, Weyl, Besicovitch and mean (and in this order these are increasingly weaker notions of almost periodicity). Now, of course, any other concept of almost periodicity for a function could also be taken as the starting point of the theory. Then, some of our considerations will easily carry over. This is discussed in this section.
$(*)$
being replaced by Bohr, weak, Weyl, Besicovitch and mean (and in this order these are increasingly weaker notions of almost periodicity). Now, of course, any other concept of almost periodicity for a function could also be taken as the starting point of the theory. Then, some of our considerations will easily carry over. This is discussed in this section.
Let
![]() $C_{\mathsf {u}} (G)$
be the set of uniformly continuous bounded functions on G and consider a dynamical system
$C_{\mathsf {u}} (G)$
be the set of uniformly continuous bounded functions on G and consider a dynamical system
![]() $(X,G)$
. Whenever we are given an
$(X,G)$
. Whenever we are given an
![]() $\mathbb A \subset C_{\mathsf {u}}(G)$
, we can define for
$\mathbb A \subset C_{\mathsf {u}}(G)$
, we can define for
![]() $p \in X$
$p \in X$
Then,
![]() $\mathbb A_p$
inherits various properties of
$\mathbb A_p$
inherits various properties of
![]() $\mathbb A$
. In particular, if
$\mathbb A$
. In particular, if
![]() $\mathbb A$
is an algebra, then so is
$\mathbb A$
is an algebra, then so is
![]() $\mathbb A_p$
and if
$\mathbb A_p$
and if
![]() $1 \in \mathbb A$
then
$1 \in \mathbb A$
then
![]() $\mathbb A_p$
contains the constant function
$\mathbb A_p$
contains the constant function
![]() $1$
. Moreover, if
$1$
. Moreover, if
![]() $\mathbb A$
is closed in
$\mathbb A$
is closed in
![]() $(C_{\mathsf {u}}(G), \| \cdot \|_\infty )$
, then
$(C_{\mathsf {u}}(G), \| \cdot \|_\infty )$
, then
![]() $\mathbb A_p$
is closed in
$\mathbb A_p$
is closed in
![]() $(C(X), \| \cdot \|_\infty )$
. Then, as abstraction of Lemma 3.7 (with the same proof), we obtain the following lemma.
$(C(X), \| \cdot \|_\infty )$
. Then, as abstraction of Lemma 3.7 (with the same proof), we obtain the following lemma.
Lemma 8.1. Let
![]() $\mathbb A$
be a closed subalgebra of
$\mathbb A$
be a closed subalgebra of
![]() $C_{\mathsf {u}}(G)$
containing the constant function 1. Then, the following assertions are equivalent for
$C_{\mathsf {u}}(G)$
containing the constant function 1. Then, the following assertions are equivalent for
![]() $p\in X$
.
$p\in X$
.
-
(i)
 $\mathbb A_p =C(X)$
.
$\mathbb A_p =C(X)$
. -
(ii)
 $\mathbb A_p$
separates the points of
$\mathbb A_p$
separates the points of
 $\overline {Gp}$
.
$\overline {Gp}$
. -
(iii) For each
 $s \in G$
the function
$s \in G$
the function
 $d^{(s)} \in C(X)$
with
$d^{(s)} \in C(X)$
with
 $d^{(s)} (y):= d(sp,y)$
belongs to
$d^{(s)} (y):= d(sp,y)$
belongs to
 $\mathbb A_p$
.
$\mathbb A_p$
.
A particular way to obtain a closed algebra
![]() $\mathbb A$
is by suitable seminorms. This is discussed next: call a seminorm N on
$\mathbb A$
is by suitable seminorms. This is discussed next: call a seminorm N on
![]() $C_{\mathsf {u}} (G)$
admissible if it is G-invariant and satisfies:
$C_{\mathsf {u}} (G)$
admissible if it is G-invariant and satisfies:
-
•
 $N(f) \leq N(g)$
whenever
$N(f) \leq N(g)$
whenever
 $|f|\leq g$
;
$|f|\leq g$
; -
•
 $N(1) = 1$
.
$N(1) = 1$
.
Note that any admissible seminorm N satisfies
![]() $N\leq \|\cdot \|_\infty $
(as
$N\leq \|\cdot \|_\infty $
(as
![]() $|f|\leq \|f\|_\infty \cdot 1$
).
$|f|\leq \|f\|_\infty \cdot 1$
).
Remark (Examples).
It is not hard to see that
![]() $\|\cdot \|_\infty $
and
$\|\cdot \|_\infty $
and
![]() $ \overline {M}\circ |\cdot |$
as well as
$ \overline {M}\circ |\cdot |$
as well as
 $$ \begin{align*} N(f):= \limsup_{n\to\infty} \sup_{t \in G} \frac{1}{|B_n|} \int_{t+B_n} |f(t) | \, d t \end{align*} $$
$$ \begin{align*} N(f):= \limsup_{n\to\infty} \sup_{t \in G} \frac{1}{|B_n|} \int_{t+B_n} |f(t) | \, d t \end{align*} $$
are admissible seminorms on
![]() $C_u (G)$
.
$C_u (G)$
.
Definition 8.2
-
(a) We say that an
 $f\in C_u (G)$
is N-almost periodic if for any
$f\in C_u (G)$
is N-almost periodic if for any
 $\varepsilon>0$
the set is relatively dense in G.
$\varepsilon>0$
the set is relatively dense in G. $$ \begin{align*}\{t\in G: N(|f - f(\cdot - t)|) <\varepsilon\}\end{align*} $$
$$ \begin{align*}\{t\in G: N(|f - f(\cdot - t)|) <\varepsilon\}\end{align*} $$
-
(b) We say that an
 $f\in C_u (G)$
is N-trig almost periodic if for any
$f\in C_u (G)$
is N-trig almost periodic if for any
 $\varepsilon>0$
, there exists some trigonometric polynomial P such that
$\varepsilon>0$
, there exists some trigonometric polynomial P such that
 $N(|f-P|) <\varepsilon $
.
$N(|f-P|) <\varepsilon $
.
Lemma 8.3. Let N be an admissible seminorm. Then,
and
are closed subalgebras of
![]() $C_{\mathsf {u}}(G)$
. Both subalgebras contain the Bohr almost periodic functions and
$C_{\mathsf {u}}(G)$
. Both subalgebras contain the Bohr almost periodic functions and
![]() $\mathbb A^T \subseteq \mathbb A^N$
holds.
$\mathbb A^T \subseteq \mathbb A^N$
holds.
In particular,
![]() $1 \in \mathbb A^N$
.
$1 \in \mathbb A^N$
.
Proof. The statement on
![]() $\mathbb A^N$
is an abstraction of Theorem B.3 in our context. It can be shown by replacing
$\mathbb A^N$
is an abstraction of Theorem B.3 in our context. It can be shown by replacing
![]() $M\circ |\cdot |$
with N in the proof of this theorem. Similarly, the statement on
$M\circ |\cdot |$
with N in the proof of this theorem. Similarly, the statement on
![]() $\mathbb A^T$
is an abstraction of Lemma C.2 in our context and can be shown by mimicking the proof of that lemma. This also gives the last statement.
$\mathbb A^T$
is an abstraction of Lemma C.2 in our context and can be shown by mimicking the proof of that lemma. This also gives the last statement.
Definition 8.4. (N-almost periodic points)
Let
![]() $(X,G)$
be a dynamical system and let N be an admissible seminorm on
$(X,G)$
be a dynamical system and let N be an admissible seminorm on
![]() $C_u (G)$
. We say, that an
$C_u (G)$
. We say, that an
![]() $x\in X$
is N-almost periodic if
$x\in X$
is N-almost periodic if
![]() $f_x$
is N-almost periodic for any
$f_x$
is N-almost periodic for any
![]() $f\in C(X)$
, that is, if
$f\in C(X)$
, that is, if
![]() $\mathbb A^N_x = C(X)$
holds.
$\mathbb A^N_x = C(X)$
holds.
For a continuous metric d on X and
![]() $x\in X$
we define
$x\in X$
we define
Reasoning as in §3, we can infer that for any continuous metric d the function
![]() $d^{N,x}$
is uniformly continuous. Having set things up, we can now discuss the following abstraction of the results in §3 (where we include some details for the convenience of the reader).
$d^{N,x}$
is uniformly continuous. Having set things up, we can now discuss the following abstraction of the results in §3 (where we include some details for the convenience of the reader).
Analogously to Lemma 3.2 we find the following.
Lemma 8.5. Let
![]() $(X,G)$
be a dynamical system. Let N be admissible. Let d be a continuous metric on X. Then, the following assertions for
$(X,G)$
be a dynamical system. Let N be admissible. Let d be a continuous metric on X. Then, the following assertions for
![]() $x\in X$
are equivalent.
$x\in X$
are equivalent.
-
(i) For any
 $\varepsilon>0$
the set is relatively dense.
$\varepsilon>0$
the set is relatively dense. $$ \begin{align*}\{t\in G : d^{N,x} (t) < \varepsilon\}\end{align*} $$
$$ \begin{align*}\{t\in G : d^{N,x} (t) < \varepsilon\}\end{align*} $$
-
(ii) The function
 $d^{N,x}$
is Bohr almost periodic.
$d^{N,x}$
is Bohr almost periodic.
The following is an abstraction of both the equivalence between assertions (i) and (ii) in Lemma 3.7 (with
![]() $N = \overline {M} \circ |\cdot |$
) and Theorem 6.10 (with
$N = \overline {M} \circ |\cdot |$
) and Theorem 6.10 (with
![]() $N=\|\cdot \|_\infty $
).
$N=\|\cdot \|_\infty $
).
Theorem 8.6. Let
![]() $(X,G)$
be a dynamical system. Let N be admissible. Then, for
$(X,G)$
be a dynamical system. Let N be admissible. Then, for
![]() $x\in X$
the following assertions are equivalent.
$x\in X$
the following assertions are equivalent.
-
(i) The point x is N-almost periodic.
-
(ii) There exists a continuous metric d on X such that
 $d^{N,x}$
is Bohr almost periodic.
$d^{N,x}$
is Bohr almost periodic. -
(iii) For every continuous metric d on X the function0
 $d^{N,x}$
is Bohr almost periodic.
$d^{N,x}$
is Bohr almost periodic.
Remark. As X is a compact metric space, a metric on X is continuous if and only if it generates the topology.
Proof. (iii)
![]() $\Longrightarrow $
(ii): This is clear.
$\Longrightarrow $
(ii): This is clear.
(ii)
![]() $\Longrightarrow $
(iii): This is the analog of Lemma 3.4 in our context. It can be shown by a variant of the proof of that lemma. Some extra effort is needed as N is not defined on measurable bounded functions but only on
$\Longrightarrow $
(iii): This is the analog of Lemma 3.4 in our context. It can be shown by a variant of the proof of that lemma. Some extra effort is needed as N is not defined on measurable bounded functions but only on
![]() $C_{\mathsf {u}} (G)$
. This is tackled by means of Urysohn’s lemma. As every locally compact group is a normal space, this lemma allows one to separate arbitrary closed disjoint sets by continuous functions and this is what we use. We now present the details.
$C_{\mathsf {u}} (G)$
. This is tackled by means of Urysohn’s lemma. As every locally compact group is a normal space, this lemma allows one to separate arbitrary closed disjoint sets by continuous functions and this is what we use. We now present the details.
Let e be any metric on X such that
![]() $e^{N,x}$
is almost periodic and let d be any other metric on X, such that
$e^{N,x}$
is almost periodic and let d be any other metric on X, such that
![]() $d,e$
generate the topology. Without loss of generality we can assume that
$d,e$
generate the topology. Without loss of generality we can assume that
![]() $d, e \leq 1$
. Let
$d, e \leq 1$
. Let
![]() $\varepsilon>0$
be arbitrary. By Lemma 8.5, it suffices to show that the set of
$\varepsilon>0$
be arbitrary. By Lemma 8.5, it suffices to show that the set of
![]() $t\in G$
with
$t\in G$
with
![]() $d^{N,x}(t)\leq \varepsilon $
is relatively dense.
$d^{N,x}(t)\leq \varepsilon $
is relatively dense.
Choose
![]() $\delta '>0$
with
$\delta '>0$
with
![]() $d(y,z) < {\varepsilon }/{2}$
whenever
$d(y,z) < {\varepsilon }/{2}$
whenever
![]() $e(y,z) <\delta '$
. Set
$e(y,z) <\delta '$
. Set
Let
![]() $t\in G$
be so that
$t\in G$
be so that
![]() $e^{N,x}(t)< \delta $
. By Lemma 8.5 the set of such
$e^{N,x}(t)< \delta $
. By Lemma 8.5 the set of such
![]() $t\in G$
is relatively dense. Thus, it remains to show
$t\in G$
is relatively dense. Thus, it remains to show
![]() $d^{N,x}(t)<\varepsilon $
for any such
$d^{N,x}(t)<\varepsilon $
for any such
![]() $t\in G$
. Define
$t\in G$
. Define
![]() $e_{t,x}$
and
$e_{t,x}$
and
![]() $d_{t,x}$
on G by
$d_{t,x}$
on G by
![]() $e_{t,x}(s):=e(sx,(t+s)x)$
and
$e_{t,x}(s):=e(sx,(t+s)x)$
and
![]() $d_{t,x}(s):=d(sx,(t+s)x)$
. Set
$d_{t,x}(s):=d(sx,(t+s)x)$
. Set
 $$ \begin{align*} A:=\bigg\{ s : e_{t,x} \geq \delta' \bigg\} \,;\quad B:=\bigg\{ s : e_{t,x} \leq \frac{\delta'}{2} \bigg\}. \end{align*} $$
$$ \begin{align*} A:=\bigg\{ s : e_{t,x} \geq \delta' \bigg\} \,;\quad B:=\bigg\{ s : e_{t,x} \leq \frac{\delta'}{2} \bigg\}. \end{align*} $$
Then, by Urysohn’s lemma, there exists some continuous function
![]() $f: G \to [0,1]$
such that
$f: G \to [0,1]$
such that
![]() $f(x)=1$
for all
$f(x)=1$
for all
![]() $x\in A$
and
$x\in A$
and
![]() $f(x)=0$
for all
$f(x)=0$
for all
![]() $x \in B$
. Set
$x \in B$
. Set
![]() $g:=1-f$
. Then,
$g:=1-f$
. Then,
![]() $ e_{t,x} \geq {\delta '}/{2} f$
and, hence,
$ e_{t,x} \geq {\delta '}/{2} f$
and, hence,
![]() $ {\delta '}/{2} N(f) \leq N(e_{t,x}) \leq \delta $
, showing
$ {\delta '}/{2} N(f) \leq N(e_{t,x}) \leq \delta $
, showing
Moreover,
![]() $d_{t,x}(s)g(s) \leq {\varepsilon }/{2}$
. Indeed, if
$d_{t,x}(s)g(s) \leq {\varepsilon }/{2}$
. Indeed, if
![]() $s \in A$
, then
$s \in A$
, then
![]() $g(s)=0$
by the definition of g, and if
$g(s)=0$
by the definition of g, and if
![]() $s \notin A$
, then
$s \notin A$
, then
![]() $ d_{t,x}(s) \leq {\varepsilon }/{2}$
by our choice of
$ d_{t,x}(s) \leq {\varepsilon }/{2}$
by our choice of
![]() $\delta '$
. This shows
$\delta '$
. This shows
Therefore, using
![]() $d \leq 1$
we obtain
$d \leq 1$
we obtain
(i)
![]() $\Longrightarrow $
(ii): This can be shown as (ii)
$\Longrightarrow $
(ii): This can be shown as (ii)
![]() $\Longrightarrow $
(i) in Lemma 3.7.
$\Longrightarrow $
(i) in Lemma 3.7.
(ii)
![]() $\Longrightarrow $
(i): As in the proof of (i)
$\Longrightarrow $
(i): As in the proof of (i)
![]() $\Longrightarrow $
(iv) of Lemma 3.7 we infer from assertion (ii) that
$\Longrightarrow $
(iv) of Lemma 3.7 we infer from assertion (ii) that
![]() $d^{z}_x$
is N-almost periodic for any
$d^{z}_x$
is N-almost periodic for any
![]() $z\in X$
. Now, assertion (i) follows from Lemma 8.1.
$z\in X$
. Now, assertion (i) follows from Lemma 8.1.
Corollary 8.7. Let
![]() $(X,G,m)$
be a dynamical system with metric d. Let N be an admissible seminorm and let
$(X,G,m)$
be a dynamical system with metric d. Let N be an admissible seminorm and let
![]() $x\in X$
be N-almost periodic. If
$x\in X$
be N-almost periodic. If
holds for all
![]() $f\in C(X)$
, then
$f\in C(X)$
, then
![]() $(X,G,m)$
has pure point spectrum.
$(X,G,m)$
has pure point spectrum.
Remark. Note that the assumption holds whenever there exists a F ølner sequence
![]() $(B_n)$
along which Birkhoff’s ergodic theorem holds and N satisfies
$(B_n)$
along which Birkhoff’s ergodic theorem holds and N satisfies
![]() $\overline {M} \circ |\cdot | \leq N$
and x is generic with respect to m.
$\overline {M} \circ |\cdot | \leq N$
and x is generic with respect to m.
Proof. As x is N-almost periodic the preceding theorem (combined with Lemma 8.5) gives that for any
![]() $\varepsilon>0$
the set of
$\varepsilon>0$
the set of
![]() $t\in G$
with
$t\in G$
with
![]() $ d^{N,x}(t)<\varepsilon $
is relatively dense. By using the assumption on N with
$ d^{N,x}(t)<\varepsilon $
is relatively dense. By using the assumption on N with
![]() $f(y) = d(y,ty)$
(for
$f(y) = d(y,ty)$
(for
![]() $t\in G$
fixed), we furthermore find for the function
$t\in G$
fixed), we furthermore find for the function
the inequality
for all
![]() $t\in G$
. Hence, for any
$t\in G$
. Hence, for any
![]() $\varepsilon>0$
the set of
$\varepsilon>0$
the set of
![]() $t\in G$
with
$t\in G$
with
![]() $\underline {d}(t) <\varepsilon $
is relatively dense as well. This gives us that
$\underline {d}(t) <\varepsilon $
is relatively dense as well. This gives us that
![]() $\underline {d}$
is Bohr almost periodic and the desired statement on pure point spectrum follows from the main result of [Reference Lenz29] (compare with the proof of Theorem 3.8 as well).
$\underline {d}$
is Bohr almost periodic and the desired statement on pure point spectrum follows from the main result of [Reference Lenz29] (compare with the proof of Theorem 3.8 as well).
Acknowledgements
Parts of this work were done while D.L. was visiting the department of mathematics in Geneva in 2019. He would like to thank the department for hospitality. He would also like to acknowledge most inspiring discussions with Gerhard Keller and Michael Baake at the workshop on Model Sets and Aperiodic Order in Durham in 2018. Part of the work was done when T.S. and N.S. visited Friedrich-Schiller-Universität Jena, and they would like to thank the Department of Mathematics for hospitality. The work was supported by DFG with grant 415818660(TS) and by NSERC with grants 03762-2014 and 2020-00038(NS), and the authors are grateful for the support.
A Appendix. Bohr almost periodic functions
In this section, we briefly present some background on Bohr almost periodic function. This is completely standard and can be found in many places. We include a discussion here in order to be self-contained and to set the perspective on the weaker (and less well-known) notions of almost periodicity underlying our considerations. For more details, we refer the reader to [Reference Corduneanu9, Reference Moody, Strungaru, Baake and Grimm35].
Let G be a locally compact abelian group. Recall from §2 that a continuous function
![]() $f : G\longrightarrow \mathbb {C}$
is called Bohr almost periodic if for any
$f : G\longrightarrow \mathbb {C}$
is called Bohr almost periodic if for any
![]() $\varepsilon>0$
the set of
$\varepsilon>0$
the set of
![]() $t\in G$
with
$t\in G$
with
is relatively dense. Any such
![]() $t\in G$
is then called an
$t\in G$
is then called an
![]() $\varepsilon $
-almost period of f. It turns out that a continuous
$\varepsilon $
-almost period of f. It turns out that a continuous
![]() $f : G\longrightarrow \mathbb {C}$
is Bohr almost periodic if and only if
$f : G\longrightarrow \mathbb {C}$
is Bohr almost periodic if and only if
![]() $\overline {\{f(\cdot - t) : t\in G\}}$
is compact, where the closure is taken with respect to the supremum norm. It is not hard to see that any Bohr almost periodic function is bounded and uniformly continuous. Moreover, the Bohr almost periodic functions form a closed subalgebra of the algebra of all uniformly continuous bounded functions on G. The main structural result on Bohr almost periodic functions is that a function f is Bohr almost periodic if and only if for any
$\overline {\{f(\cdot - t) : t\in G\}}$
is compact, where the closure is taken with respect to the supremum norm. It is not hard to see that any Bohr almost periodic function is bounded and uniformly continuous. Moreover, the Bohr almost periodic functions form a closed subalgebra of the algebra of all uniformly continuous bounded functions on G. The main structural result on Bohr almost periodic functions is that a function f is Bohr almost periodic if and only if for any
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
and
$\xi _1,\ldots , \xi _k\in \widehat {G}$
and
![]() $c_1, \ldots , c_k\in \mathbb {C}$
with
$c_1, \ldots , c_k\in \mathbb {C}$
with
 $$ \begin{align} \bigg\| f - \sum_{j=1}^k c_j \xi_j\bigg\|_\infty < \varepsilon. \end{align} $$
$$ \begin{align} \bigg\| f - \sum_{j=1}^k c_j \xi_j\bigg\|_\infty < \varepsilon. \end{align} $$
The basic idea of the weaker concepts of almost periodicity discussed in the subsequent sections is to replace the supremum norm
![]() $\|\cdot \|_\infty $
in
$\|\cdot \|_\infty $
in
![]() $(\spadesuit )$
and
$(\spadesuit )$
and
![]() $(\heartsuit )$
by suitable (semi)norms arising by averaging procedures.
$(\heartsuit )$
by suitable (semi)norms arising by averaging procedures.
B Appendix. Mean almost periodic functions
The main result of this appendix shows that the bounded uniformly continuous mean almost periodic functions form a closed subalgebra of the algebra of bounded uniformly continuous functions on G. This is certainly well known and a proof can be given by standard means. For the convenience of the reader and in order to keep this article self-contained we include a discussion in the following. As our article deals with abelian groups, we assume that the group G in the following is abelian. Note, however, that this is not used in the proofs.
We start with a general result on discrete geometry of groups.
Proposition B.1. Let G be a locally compact abelian group. Let D and E be relatively dense subsets of G and V a relatively compact open neighborhood of the neutral element. Then,
![]() $ ((D-D) + V) \cap ((E - E) + V) $
is relatively dense.
$ ((D-D) + V) \cap ((E - E) + V) $
is relatively dense.
Proof. As both D and E are relatively dense, we can choose an open relatively compact set
![]() $U\subset G$
with the property that any translate of U intersects both D and E. As addition is continuous on G, we can choose furthermore a relatively compact open neighborhood W with
$U\subset G$
with the property that any translate of U intersects both D and E. As addition is continuous on G, we can choose furthermore a relatively compact open neighborhood W with
![]() $W = -W$
and
$W = -W$
and
![]() $W + W \subset V$
. As U is relatively compact, there exist
$W + W \subset V$
. As U is relatively compact, there exist
![]() $N\in \mathbb {N}$
and
$N\in \mathbb {N}$
and
![]() $z_1,\ldots z_N\in G$
with
$z_1,\ldots z_N\in G$
with
 $$ \begin{align*}U = \bigcup_{n=1}^N (z_n + W) \cap U.\end{align*} $$
$$ \begin{align*}U = \bigcup_{n=1}^N (z_n + W) \cap U.\end{align*} $$
Consider now an arbitrary
![]() $t\in D$
. Then, there exists an
$t\in D$
. Then, there exists an
![]() $s\in E$
with
$s\in E$
with
![]() $t - s \in U$
. Hence, for any
$t - s \in U$
. Hence, for any
![]() $t\in D$
we can find
$t\in D$
we can find
![]() $s_t \in E$
and
$s_t \in E$
and
![]() $n_t\in \{1,\ldots , N\}$
with
$n_t\in \{1,\ldots , N\}$
with
Fix now for each
![]() $n\in \{1,\ldots , N\}$
elements
$n\in \{1,\ldots , N\}$
elements
![]() $t_n\in D$
and
$t_n\in D$
and
![]() $s_n\in E$
with
$s_n\in E$
with
(If some of the n does not admit elements, we just remove this n from our list.) Then, for any
![]() $t\in D$
we can find
$t\in D$
we can find
![]() $s_t\in E$
and
$s_t\in E$
and
![]() $n\in \{1,\ldots , N\}$
such that both
$n\in \{1,\ldots , N\}$
such that both
![]() $ t- s_t$
and
$ t- s_t$
and
![]() $ t_n - s_n$
belong to
$ t_n - s_n$
belong to
![]() $z_n + W$
. Hence, we find
$z_n + W$
. Hence, we find
for suitable
![]() $w,w'\in W$
. This gives
$w,w'\in W$
. This gives
with
![]() $v = w' {\kern-1.2pt}-{\kern-1.2pt} w {\kern-1.2pt}\in{\kern-1.2pt} W {\kern-1.2pt}-{\kern-1.2pt} W {\kern-1.2pt}\subset{\kern-1.2pt} V$
. Now, we clearly have
$v = w' {\kern-1.2pt}-{\kern-1.2pt} w {\kern-1.2pt}\in{\kern-1.2pt} W {\kern-1.2pt}-{\kern-1.2pt} W {\kern-1.2pt}\subset{\kern-1.2pt} V$
. Now, we clearly have
![]() $t {\kern-1.2pt}-{\kern-1.2pt} t_n {\kern-1.2pt}\in{\kern-1.2pt} (D{\kern-1.2pt}-{\kern-1.2pt}D) {\kern-1.2pt}+{\kern-1.2pt} V$
and
$t {\kern-1.2pt}-{\kern-1.2pt} t_n {\kern-1.2pt}\in{\kern-1.2pt} (D{\kern-1.2pt}-{\kern-1.2pt}D) {\kern-1.2pt}+{\kern-1.2pt} V$
and
![]() $(s_t {\kern-1.2pt}-{\kern-1.2pt} s_n) {\kern-1.2pt}+ v\in (E-E) + V$
. Moreover, the set of all
$(s_t {\kern-1.2pt}-{\kern-1.2pt} s_n) {\kern-1.2pt}+ v\in (E-E) + V$
. Moreover, the set of all
![]() $t - t_n$
is relatively dense as t is an arbitrary element of the relatively dense D and there are only finitely many
$t - t_n$
is relatively dense as t is an arbitrary element of the relatively dense D and there are only finitely many
![]() $t_n$
. This finishes the proof.
$t_n$
. This finishes the proof.
Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Let f be a uniformly continuous bounded function on G. Let
$(B_n)$
be a Følner sequence on G. Let f be a uniformly continuous bounded function on G. Let
![]() $\varepsilon>0$
be given. As usual we say that a
$\varepsilon>0$
be given. As usual we say that a
![]() $t\in G$
is an
$t\in G$
is an
![]() $\varepsilon $
-almost period of f if
$\varepsilon $
-almost period of f if
Denote the set of all
![]() $\varepsilon $
-almost periods of f by
$\varepsilon $
-almost periods of f by
![]() $ \mbox {AP}(f,\varepsilon )$
. Then, it is not hard to see that
$ \mbox {AP}(f,\varepsilon )$
. Then, it is not hard to see that
A uniformly continuous bounded
![]() $f : G\longrightarrow \mathbb {C}$
is mean almost periodic if for any
$f : G\longrightarrow \mathbb {C}$
is mean almost periodic if for any
![]() $\varepsilon>0$
the set
$\varepsilon>0$
the set
![]() $\mbox {AP}(f,\varepsilon )$
is relatively dense.
$\mbox {AP}(f,\varepsilon )$
is relatively dense.
Lemma B.2. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Let a natural number n and uniformly continuous bounded mean almost periodic functions
$(B_n)$
be a Følner sequence on G. Let a natural number n and uniformly continuous bounded mean almost periodic functions
![]() $f_1, \ldots , f_n$
on G be given. Then, the set
$f_1, \ldots , f_n$
on G be given. Then, the set
 $$ \begin{align*}\bigcap_{k=1}^n \operatorname{AP}(f_k,\varepsilon)\end{align*} $$
$$ \begin{align*}\bigcap_{k=1}^n \operatorname{AP}(f_k,\varepsilon)\end{align*} $$
is relatively dense in G for any
![]() $\varepsilon>0$
.
$\varepsilon>0$
.
Proof. This is shown by induction in n. The case
![]() $n =1$
is clear. Thus, assume now the statement holds for a chosen n. Let
$n =1$
is clear. Thus, assume now the statement holds for a chosen n. Let
![]() $\varepsilon>0$
and uniformly continuous functions
$\varepsilon>0$
and uniformly continuous functions
![]() $f_1,\ldots , f_{n+1}$
be given. Then, the set
$f_1,\ldots , f_{n+1}$
be given. Then, the set
![]() $D:=\bigcap _{k=1}^n \mbox {AP}(f_k, \varepsilon / 3)$
is relatively dense by assumption. As the functions
$D:=\bigcap _{k=1}^n \mbox {AP}(f_k, \varepsilon / 3)$
is relatively dense by assumption. As the functions
![]() $f_k$
,
$f_k$
,
![]() $k=1,\ldots , n+1$
, are uniformly continuous we can find an open relatively compact neighborhood V of the neutral element such that
$k=1,\ldots , n+1$
, are uniformly continuous we can find an open relatively compact neighborhood V of the neutral element such that
for all
![]() $s\in V$
and
$s\in V$
and
![]() $k=1,\ldots , n+1$
. Set
$k=1,\ldots , n+1$
. Set
![]() $E:=\mbox {AP}(f_{n+1},\varepsilon /3)$
. Then, the previous proposition gives that
$E:=\mbox {AP}(f_{n+1},\varepsilon /3)$
. Then, the previous proposition gives that
is relatively dense. On the other hand, it is not hard to see that
This finishes the proof.
Theorem B.3. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Then, the set of all uniformly continuous bounded mean almost periodic functions is invariant under taking complex conjugates and a closed subalgebra of the uniformly continuous bounded functions on G equipped with
$(B_n)$
be a Følner sequence on G. Then, the set of all uniformly continuous bounded mean almost periodic functions is invariant under taking complex conjugates and a closed subalgebra of the uniformly continuous bounded functions on G equipped with
![]() $\|\cdot \|_\infty $
.
$\|\cdot \|_\infty $
.
Proof. We have to show that the set in question is closed under complex conjugation, sums, products, multiplication by scalars and uniform convergence.
It is not hard to see that the set in question is closed under complex conjugation, uniform convergence and multiplication by scalars.
We next show that it is closed under sums: let
![]() $f,g$
be mean almost periodic uniformly continuous bounded functions. Then, the previous lemma easily gives that
$f,g$
be mean almost periodic uniformly continuous bounded functions. Then, the previous lemma easily gives that
![]() $f + g$
is also mean almost periodic.
$f + g$
is also mean almost periodic.
Finally, we deal with products: let
![]() $f,g$
be mean almost periodic uniformly continuous bounded functions. Then, a short computation gives for any
$f,g$
be mean almost periodic uniformly continuous bounded functions. Then, a short computation gives for any
![]() $t\in G$
$t\in G$
 $$ \begin{align*} |f(s) g(s) - f(s-t) g(s-t)| &\leq |f(s) g(s) - f(s) g(s-t)|\\ &\quad +|f(s)g(s-t) - f(s-t) g(s-t)|\\ &\leq \|f\|_\infty |g(s) - g(s-t)|+ \|g\|_\infty |f(s) - f(s-t)|. \end{align*} $$
$$ \begin{align*} |f(s) g(s) - f(s-t) g(s-t)| &\leq |f(s) g(s) - f(s) g(s-t)|\\ &\quad +|f(s)g(s-t) - f(s-t) g(s-t)|\\ &\leq \|f\|_\infty |g(s) - g(s-t)|+ \|g\|_\infty |f(s) - f(s-t)|. \end{align*} $$
From this we easily obtain
Now, the desired statement follows easily from the preceding lemma.
The last statement is clear.
For later use we also note the following proposition.
Proposition B.4. Let
![]() $(f_n)$
be a sequence of uniformly continuous bounded mean almost periodic functions on G with
$(f_n)$
be a sequence of uniformly continuous bounded mean almost periodic functions on G with
![]() $\|f_n\|\leq 1$
for all n. Let
$\|f_n\|\leq 1$
for all n. Let
![]() $c_n>0$
with
$c_n>0$
with
![]() $\sum _{n=1}^{\infty } c_n <\infty $
be given. Then, there exists for any
$\sum _{n=1}^{\infty } c_n <\infty $
be given. Then, there exists for any
![]() $\varepsilon>0$
a relatively dense set D in G with
$\varepsilon>0$
a relatively dense set D in G with
 $$ \begin{align*}\overline{M}\bigg(\sum_{n=1}^{\infty} c_n |f - f(\cdot -t)|\bigg) <\varepsilon\end{align*} $$
$$ \begin{align*}\overline{M}\bigg(\sum_{n=1}^{\infty} c_n |f - f(\cdot -t)|\bigg) <\varepsilon\end{align*} $$
for all
![]() $t\in D$
.
$t\in D$
.
Proof. Choose
![]() $n_0$
large enough so that
$n_0$
large enough so that
![]() $\sum _{k=n_0 +1}^\infty c_k < \varepsilon /4$
. Then,
$\sum _{k=n_0 +1}^\infty c_k < \varepsilon /4$
. Then,
![]() $\sum _{n=n_0 +1}^\infty c_n \|f - f(\cdot -t)\|_\infty < \varepsilon /2 $
by assumption on the
$\sum _{n=n_0 +1}^\infty c_n \|f - f(\cdot -t)\|_\infty < \varepsilon /2 $
by assumption on the
![]() $f_n$
and the
$f_n$
and the
![]() $c_n$
. By Lemma B.2 there exists a relatively dense set D in G with
$c_n$
. By Lemma B.2 there exists a relatively dense set D in G with
![]() $\overline {M}( |f_k - f_k (\cdot -t)|) <{\varepsilon }/{2 n_0}$
for
$\overline {M}( |f_k - f_k (\cdot -t)|) <{\varepsilon }/{2 n_0}$
for
![]() $k = 1,\ldots , n_0$
. Now, the statement follows easily.
$k = 1,\ldots , n_0$
. Now, the statement follows easily.
Remark. The considerations of this section carry over when
![]() $\overline {M}\circ |\cdot | $
is replaced by any invariant seminorm N on the algebra of bounded uniformly continuous functions on G satisfying:
$\overline {M}\circ |\cdot | $
is replaced by any invariant seminorm N on the algebra of bounded uniformly continuous functions on G satisfying:
-
•
 $N(f) \leq N(g)$
whenever
$N(f) \leq N(g)$
whenever
 $|f|\leq g$
;
$|f|\leq g$
; -
•
 $N(1) =1$
.
$N(1) =1$
.
This point is taken up in §8.
C Appendix. Besicovitch almost periodic functions and existence of means
We consider a
![]() $\sigma $
-compact locally compact abelian group G together with a Følner sequence
$\sigma $
-compact locally compact abelian group G together with a Følner sequence
![]() $(B_n)$
. Our aim is to study the set of uniformly continuous bounded functions
$(B_n)$
. Our aim is to study the set of uniformly continuous bounded functions
![]() $f : G\longrightarrow \mathbb {C}$
, which are Besicovitch almost periodic, that is, they satisfy that for any
$f : G\longrightarrow \mathbb {C}$
, which are Besicovitch almost periodic, that is, they satisfy that for any
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
and
$\xi _1,\ldots , \xi _k\in \widehat {G}$
and
![]() $c_1,\ldots ,c_k\in \mathbb {C}$
with
$c_1,\ldots ,c_k\in \mathbb {C}$
with
 $$ \begin{align*}\overline{M} \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg)< \varepsilon.\end{align*} $$
$$ \begin{align*}\overline{M} \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg)< \varepsilon.\end{align*} $$
For an in-depth study of these functions, we the reader refer to [Reference Lenz, Spindeler and Strungaru31]. Here, we briefly summarize what is needed for the purposes of the present article.
Proposition C.1. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Then, any uniformly continuous bounded Besicovitch almost periodic function is mean almost periodic.
$(B_n)$
be a Følner sequence on G. Then, any uniformly continuous bounded Besicovitch almost periodic function is mean almost periodic.
Proof. Let
![]() $\varepsilon>0$
be given. Choose
$\varepsilon>0$
be given. Choose
![]() $c_1,\ldots , c_k\in \mathbb {C} $
and
$c_1,\ldots , c_k\in \mathbb {C} $
and
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
such that
$\xi _1,\ldots , \xi _k\in \widehat {G}$
such that
![]() $P:=\sum _{j=1}^k c_j \xi _j$
satisfies
$P:=\sum _{j=1}^k c_j \xi _j$
satisfies
As
![]() $\overline {M}$
is invariant this inequality will then continue to hold if f is replaced by
$\overline {M}$
is invariant this inequality will then continue to hold if f is replaced by
![]() $f(\cdot -t)$
and P is replaced by
$f(\cdot -t)$
and P is replaced by
![]() $P(\cdot - t)$
for any
$P(\cdot - t)$
for any
![]() $t\in G$
. Now, clearly P is Bohr almost periodic. Hence, there exists a relatively dense set
$t\in G$
. Now, clearly P is Bohr almost periodic. Hence, there exists a relatively dense set
![]() $R\subset G$
with
$R\subset G$
with
![]() $\|P - P(\cdot - t)\|_\infty <\varepsilon $
for all
$\|P - P(\cdot - t)\|_\infty <\varepsilon $
for all
![]() $t\in R$
. This easily gives
$t\in R$
. This easily gives
for all
![]() $t\in R$
.
$t\in R$
.
From the definition and simple algebraic manipulations, we infer the following.
Lemma C.2. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Then, the set of all uniformly continuous bounded Besicovitch almost periodic functions is invariant under taking complex conjugates and a closed subalgebra of the uniformly continuous bounded functions on G equipped with
$(B_n)$
be a Følner sequence on G. Then, the set of all uniformly continuous bounded Besicovitch almost periodic functions is invariant under taking complex conjugates and a closed subalgebra of the uniformly continuous bounded functions on G equipped with
![]() $\|\cdot \|_\infty $
. It contains all Bohr almost periodic functions and is contained in the algebra of mean almost periodic functions.
$\|\cdot \|_\infty $
. It contains all Bohr almost periodic functions and is contained in the algebra of mean almost periodic functions.
Proof. The set is clearly closed under taking limits with respect to
![]() $\|\cdot \|_\infty $
as well as under addition and taking complex conjugates. To show that it is closed under multiplication consider
$\|\cdot \|_\infty $
as well as under addition and taking complex conjugates. To show that it is closed under multiplication consider
![]() $f,g$
in this set and let
$f,g$
in this set and let
![]() $\epsilon>0$
be arbitrary. Let
$\epsilon>0$
be arbitrary. Let
![]() $P,Q$
be trigonometric polynomials so that
$P,Q$
be trigonometric polynomials so that
Define
 $$ \begin{align*} Q'(x):= \begin{cases} Q(x) & \mbox{if } |Q(x)| \leq \| g \|_\infty +1, \\[6pt] \dfrac{Q(x)}{|Q(x)|}( \| g \|_\infty +1 ) & \text{otherwise.} \end{cases} \end{align*} $$
$$ \begin{align*} Q'(x):= \begin{cases} Q(x) & \mbox{if } |Q(x)| \leq \| g \|_\infty +1, \\[6pt] \dfrac{Q(x)}{|Q(x)|}( \| g \|_\infty +1 ) & \text{otherwise.} \end{cases} \end{align*} $$
Then,
![]() $Q'$
is a Bohr almost periodic function and
$Q'$
is a Bohr almost periodic function and
![]() $|g-Q'| \leq |g-Q|$
, which gives
$|g-Q'| \leq |g-Q|$
, which gives
![]() $\overline {M}(|g-Q'|) \leq \overline {M}(|g-Q|)$
.
$\overline {M}(|g-Q'|) \leq \overline {M}(|g-Q|)$
.
As
![]() $Q'$
is Bohr almost periodic, there exists a trigonometric polynomial R such that
$Q'$
is Bohr almost periodic, there exists a trigonometric polynomial R such that
![]() $\| Q'-R \|_\infty < \min \{ {\varepsilon }/({4\| f \|_\infty +1}), 1 \}$
. In particular,
$\| Q'-R \|_\infty < \min \{ {\varepsilon }/({4\| f \|_\infty +1}), 1 \}$
. In particular,
Then,
 $$ \begin{align*} \overline{M}(|fg-PR|) &\leq \overline{M}(|fg-fR|)+ \overline{M}(|fR-PR|) \\ &\leq \| f \|_\infty \overline{M}(|g-R|)+\| R \|_\infty \overline{M}(|f-P|)\\ &\leq \| f \|_\infty ( \overline{M}(|g-Q'|)+\overline{M}(|Q'-R|) ) + \frac{\varepsilon}{2} \\ &\leq \| f \|_\infty ( \overline{M}(|g-Q'|)+\| Q'-R\|_\infty )+ \frac{\varepsilon}{2}\\ & < \varepsilon. \end{align*} $$
$$ \begin{align*} \overline{M}(|fg-PR|) &\leq \overline{M}(|fg-fR|)+ \overline{M}(|fR-PR|) \\ &\leq \| f \|_\infty \overline{M}(|g-R|)+\| R \|_\infty \overline{M}(|f-P|)\\ &\leq \| f \|_\infty ( \overline{M}(|g-Q'|)+\overline{M}(|Q'-R|) ) + \frac{\varepsilon}{2} \\ &\leq \| f \|_\infty ( \overline{M}(|g-Q'|)+\| Q'-R\|_\infty )+ \frac{\varepsilon}{2}\\ & < \varepsilon. \end{align*} $$
This shows that the set in question is closed under multiplication. It clearly contains all Bohr almost periodic functions and is contained in the set of mean almost periodic functions.
Remark. The functions referred to as Besicovitch almost periodic were introduced by Besicovitch in [Reference Besicovitch8] for
![]() $G =\mathbb {R}$
. A corresponding class of functions was then studied by Følner for general locally compact abelian groups [Reference Følner14]. This class, however, does not coincide with the Besicovitch class for
$G =\mathbb {R}$
. A corresponding class of functions was then studied by Følner for general locally compact abelian groups [Reference Følner14]. This class, however, does not coincide with the Besicovitch class for
![]() $G =\mathbb {R}$
. Another approach to Besicovitch almost periodic functions is developed by Davis in [Reference Davis10]. An account of these developments with a focus on aperiodic order is given in Lagarias survey [Reference Lagarias, Baake and Moody25]. Here, we have taken a ‘shortcut’: we have not defined Besicovitch almost periodic functions by some intrinsic features. Instead we have defined them by what would be a main result in a proper theory starting with an intrinsic definition.
$G =\mathbb {R}$
. Another approach to Besicovitch almost periodic functions is developed by Davis in [Reference Davis10]. An account of these developments with a focus on aperiodic order is given in Lagarias survey [Reference Lagarias, Baake and Moody25]. Here, we have taken a ‘shortcut’: we have not defined Besicovitch almost periodic functions by some intrinsic features. Instead we have defined them by what would be a main result in a proper theory starting with an intrinsic definition.
A crucial feature of Besicovitch almost periodic function is existence of means in the following sense.
Lemma C.3. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Let
$(B_n)$
be a Følner sequence on G. Let
![]() $f: G\longrightarrow \mathbb {C}$
be a uniformly continuous, bounded Besicovitch almost periodic function. Then, the limit
$f: G\longrightarrow \mathbb {C}$
be a uniformly continuous, bounded Besicovitch almost periodic function. Then, the limit
 $$ \begin{align*} \mathrm{A}(f)=\lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} f(s)\,d s \end{align*} $$
$$ \begin{align*} \mathrm{A}(f)=\lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n} f(s)\,d s \end{align*} $$
exists.
Proof. The statement is well known for functions of the form
![]() $f = \sum _{j=1}^k c_j \xi _j$
with
$f = \sum _{j=1}^k c_j \xi _j$
with
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
,
$\xi _1,\ldots , \xi _k\in \widehat {G}$
,
![]() $c_1,\ldots , c_k\in \mathbb {C}$
. It then follows by a limiting procedure for Besicovitch almost periodic functions.
$c_1,\ldots , c_k\in \mathbb {C}$
. It then follows by a limiting procedure for Besicovitch almost periodic functions.
In fact, existence of means together with a Parseval type equality is a characterizing feature of Besicovitch almost periodic functions.
Proposition C.4. Let G be a
![]() $\sigma $
-compact locally compact abelian group and let
$\sigma $
-compact locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Let
$(B_n)$
be a Følner sequence on G. Let
![]() $f: G\longrightarrow \mathbb {C}$
be a uniformly continuous and bounded. Then, f is Besicovitch almost periodic if and only if there exists a countable set
$f: G\longrightarrow \mathbb {C}$
be a uniformly continuous and bounded. Then, f is Besicovitch almost periodic if and only if there exists a countable set
![]() $F\subset \widehat {G}$
such that the following three statements hold.
$F\subset \widehat {G}$
such that the following three statements hold.
-
• The limit
 $\mathrm {A}(|f|^2) = \lim _{n\to \infty } ({1}/{|B_n|}) \int _{B_n} |f(t)|^2 \,d t$
exists.
$\mathrm {A}(|f|^2) = \lim _{n\to \infty } ({1}/{|B_n|}) \int _{B_n} |f(t)|^2 \,d t$
exists. -
• For any
 $\xi \in F$
the limit exists.
$\xi \in F$
the limit exists. $$ \begin{align*} \mathrm{A}(f \overline{\xi}) =\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(t)\, \overline{\xi(t)} \,d t\\[-24pt] \end{align*} $$
$$ \begin{align*} \mathrm{A}(f \overline{\xi}) =\lim_{n\to \infty} \frac{1}{|B_n|} \int_{B_n} f(t)\, \overline{\xi(t)} \,d t\\[-24pt] \end{align*} $$
-
• The equality
holds. $$ \begin{align*} \mathrm{A}(|f|^2) =\sum_{\xi \in F} |\mathrm{A}(f \overline{\xi})|^2\\[-24pt] \end{align*} $$
$$ \begin{align*} \mathrm{A}(|f|^2) =\sum_{\xi \in F} |\mathrm{A}(f \overline{\xi})|^2\\[-24pt] \end{align*} $$
In this case
![]() $\mathrm {A}(f \overline {\xi })= 0$
holds for all
$\mathrm {A}(f \overline {\xi })= 0$
holds for all
![]() $\xi \in \widehat {G}\setminus F$
.
$\xi \in \widehat {G}\setminus F$
.
Proof. Let f be Besicovitch almost periodic. Clearly, any
![]() $\xi \in \widehat {G}$
is Bohr almost periodic and, hence, Besicovitch almost periodic. Thus,
$\xi \in \widehat {G}$
is Bohr almost periodic and, hence, Besicovitch almost periodic. Thus,
![]() $f\overline {\xi }$
is Besicovitch almost periodic as a product of Besicovitch almost periodic functions. Hence, the second point holds (even for all
$f\overline {\xi }$
is Besicovitch almost periodic as a product of Besicovitch almost periodic functions. Hence, the second point holds (even for all
![]() $\xi \in \widehat {G}$
). Similarly,
$\xi \in \widehat {G}$
). Similarly,
![]() $|f|^2$
is Besicovitch almost periodic. Given this, the first point follows. The last point is contained in [Reference Lenz, Spindeler and Strungaru31].
$|f|^2$
is Besicovitch almost periodic. Given this, the first point follows. The last point is contained in [Reference Lenz, Spindeler and Strungaru31].
Now, consider f satisfying the three points. Let
![]() $\xi _1,\xi _2,\ldots $
be an enumeration of the
$\xi _1,\xi _2,\ldots $
be an enumeration of the
![]() $\xi \in F$
. A computation involving the Cauchy–Schwarz inequality in the first step,
$\xi \in F$
. A computation involving the Cauchy–Schwarz inequality in the first step,
![]() $\overline {M}(1) =1$
in the second step and existence of averages A in the third step gives
$\overline {M}(1) =1$
in the second step and existence of averages A in the third step gives
 $$ \begin{align*} &\overline{M}\bigg(\bigg|f -\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j\bigg|\bigg)^2 \\ &\quad\leq \overline{M}\bigg(\bigg|f -\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j\bigg|^2\bigg) \overline{M}(1)\\ &\quad=\overline{M}\bigg(|f|^2 - f \overline{\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j} - \overline{f}\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j+ \sum_{j,k=1}^N A(f\overline{\xi_j} ) \overline{ A(f\overline{\xi_k})} \xi_j \overline{\xi_k}\bigg) \\ &\quad= \mathrm{A}(|f|^2) -\mathrm{A}\bigg( f \overline{\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j} \bigg) - \mathrm{A}\bigg( \overline{f}\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j \bigg) + \mathrm{A}\bigg( \!\sum_{j=1,k}^N\! A(f\overline{\xi_j}) \overline{A(f\overline{\xi_k})} \xi_j \overline{\xi_k}\bigg)\\ &\quad= \mathrm{A}(|f|^2) - \sum_{j=1}^N |A(f \overline{\xi})|^2\\ &\quad\to 0 \end{align*} $$
$$ \begin{align*} &\overline{M}\bigg(\bigg|f -\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j\bigg|\bigg)^2 \\ &\quad\leq \overline{M}\bigg(\bigg|f -\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j\bigg|^2\bigg) \overline{M}(1)\\ &\quad=\overline{M}\bigg(|f|^2 - f \overline{\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j} - \overline{f}\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j+ \sum_{j,k=1}^N A(f\overline{\xi_j} ) \overline{ A(f\overline{\xi_k})} \xi_j \overline{\xi_k}\bigg) \\ &\quad= \mathrm{A}(|f|^2) -\mathrm{A}\bigg( f \overline{\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j} \bigg) - \mathrm{A}\bigg( \overline{f}\sum_{j=1}^N A(f\overline{\xi_j} ) \xi_j \bigg) + \mathrm{A}\bigg( \!\sum_{j=1,k}^N\! A(f\overline{\xi_j}) \overline{A(f\overline{\xi_k})} \xi_j \overline{\xi_k}\bigg)\\ &\quad= \mathrm{A}(|f|^2) - \sum_{j=1}^N |A(f \overline{\xi})|^2\\ &\quad\to 0 \end{align*} $$
for
![]() $N\to \infty $
. Here, the penultimate step is a direct computation invoking that A is linear with
$N\to \infty $
. Here, the penultimate step is a direct computation invoking that A is linear with
![]() $A(\eta )=0$
for
$A(\eta )=0$
for
![]() $0\neq \eta \in \widehat {G}$
. Indeed, this shows that f can be approximated in mean by a trigonometric polynomial arbitrarily well. This finishes the proof.
$0\neq \eta \in \widehat {G}$
. Indeed, this shows that f can be approximated in mean by a trigonometric polynomial arbitrarily well. This finishes the proof.
D Appendix. Weyl almost periodic functions and uniform means
In this appendix, we consider a uniform type of mean.
Let
![]() $(B_n)$
be a Følner sequence in G and define for bounded
$(B_n)$
be a Følner sequence in G and define for bounded
![]() $f : G\longrightarrow \mathbb {R}$
and
$f : G\longrightarrow \mathbb {R}$
and
![]() $n\in \mathbb {N}$
$n\in \mathbb {N}$
 $$ \begin{align*} \overline{M}_n (f) := \sup_{r\in G} \frac{1}{|B_n|} \int_{B_n + r} f(t)\,d t. \end{align*} $$
$$ \begin{align*} \overline{M}_n (f) := \sup_{r\in G} \frac{1}{|B_n|} \int_{B_n + r} f(t)\,d t. \end{align*} $$
Proposition D.1. For a bounded measurable function
![]() $f:G\longrightarrow \mathbb {R}$
and
$f:G\longrightarrow \mathbb {R}$
and
![]() $\varepsilon>0$
the following assertions are equivalent.
$\varepsilon>0$
the following assertions are equivalent.
-
(i) There exists an
 $N\in \mathbb {N}$
with
$N\in \mathbb {N}$
with
 $\overline {M}_N (f) < \varepsilon $
.
$\overline {M}_N (f) < \varepsilon $
. -
(ii) There exists an
 $N_0\in \mathbb {N}$
with
$N_0\in \mathbb {N}$
with
 $\overline {M}_N (f) <\varepsilon $
for all
$\overline {M}_N (f) <\varepsilon $
for all
 $N\geq N_0$
.
$N\geq N_0$
.
Proof. (ii)
![]() $\Longrightarrow $
(i): This is clear.
$\Longrightarrow $
(i): This is clear.
(i)
![]() $\Longrightarrow $
(ii): Consider
$\Longrightarrow $
(ii): Consider
![]() $n\in \mathbb {N}$
. Define for
$n\in \mathbb {N}$
. Define for
![]() $r\in G$
$r\in G$
 $$ \begin{align*} C_{r}:= \frac{1}{|B_N|}\int_{B_N } \bigg(\int\frac{1}{|B_n|}\int_{B_n + r} f(s +t)\,d s \bigg)\,d t. \end{align*} $$
$$ \begin{align*} C_{r}:= \frac{1}{|B_N|}\int_{B_N } \bigg(\int\frac{1}{|B_n|}\int_{B_n + r} f(s +t)\,d s \bigg)\,d t. \end{align*} $$
Fubini’s theorem and the assumption (i) directly give
 $$ \begin{align*} C_{r}=\frac{1}{|B_n|}\int_{B_n + r} \bigg(\frac{1}{|B_N|}\int_{B_N } f(s +t)\,d t \bigg)\,d s \leq \frac{1}{|B_n|}\int_{B_n + r} \overline{M}_N (f)\,d s = \overline{M}_N (f). \end{align*} $$
$$ \begin{align*} C_{r}=\frac{1}{|B_n|}\int_{B_n + r} \bigg(\frac{1}{|B_N|}\int_{B_N } f(s +t)\,d t \bigg)\,d s \leq \frac{1}{|B_n|}\int_{B_n + r} \overline{M}_N (f)\,d s = \overline{M}_N (f). \end{align*} $$
On the other hand, we can easily see that (for large n) the additional averaging over
![]() $B_N$
does not play a role. More specifically, we can compute as follows:
$B_N$
does not play a role. More specifically, we can compute as follows:
 $$ \begin{align*} \bigg| C_{r} - \frac{1}{|B_n|} \int_{B_n + r} f(s)\,d s \bigg| &= \bigg| C_{r} - \frac{1}{|B_N|} \int_{B_N } \bigg(\frac{1}{|B_n|} \int_{B_n + r} f(s)\,d s\bigg)\,d t\bigg|\\ &= \bigg|\frac{1}{|B_N|}\int_{B_N } \bigg(\frac{1}{|B_n|}\int_{B_n + r} (f(s +t) - f(s) )\,d s \bigg)\,d t\bigg|\\ &\leq \frac{1}{|B_N|} \int_{B_N} 2\|f\|_\infty \frac{|(B_n + t)\, \triangle\, B_n| }{|B_n| }\,d t. \end{align*} $$
$$ \begin{align*} \bigg| C_{r} - \frac{1}{|B_n|} \int_{B_n + r} f(s)\,d s \bigg| &= \bigg| C_{r} - \frac{1}{|B_N|} \int_{B_N } \bigg(\frac{1}{|B_n|} \int_{B_n + r} f(s)\,d s\bigg)\,d t\bigg|\\ &= \bigg|\frac{1}{|B_N|}\int_{B_N } \bigg(\frac{1}{|B_n|}\int_{B_n + r} (f(s +t) - f(s) )\,d s \bigg)\,d t\bigg|\\ &\leq \frac{1}{|B_N|} \int_{B_N} 2\|f\|_\infty \frac{|(B_n + t)\, \triangle\, B_n| }{|B_n| }\,d t. \end{align*} $$
Now, due to the Følner condition the integrand in the last term can easily be seen to go pointwise to zero for
![]() $n\to \infty $
. As
$n\to \infty $
. As
![]() $B_N$
is compact, we find convergence to zero of the integral for each fixed N. As there is no dependence on
$B_N$
is compact, we find convergence to zero of the integral for each fixed N. As there is no dependence on
![]() $r\in G$
, this convergence is independent of
$r\in G$
, this convergence is independent of
![]() $r\in G$
. This easily gives the desired statement.
$r\in G$
. This easily gives the desired statement.
A bounded
![]() $f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if for all
$f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if for all
![]() $\varepsilon>0$
there exist
$\varepsilon>0$
there exist
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k\in \widehat {G}$
and
$\xi _1,\ldots , \xi _k\in \widehat {G}$
and
![]() $c_1,\ldots ,c_k\in \mathbb {C}$
with
$c_1,\ldots ,c_k\in \mathbb {C}$
with
 $$ \begin{align*}\limsup_{n\to\infty} \overline{M}_n \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
$$ \begin{align*}\limsup_{n\to\infty} \overline{M}_n \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
By the preceding proposition it is possible to replace this condition by the requirement that for each
![]() $\varepsilon>0$
there exists an
$\varepsilon>0$
there exists an
![]() $N\in \mathbb {N}$
,
$N\in \mathbb {N}$
,
![]() $k\in \mathbb {N}$
,
$k\in \mathbb {N}$
,
![]() $\xi _1,\ldots , \xi _k \in \widehat {G}$
and
$\xi _1,\ldots , \xi _k \in \widehat {G}$
and
![]() $c_1,\ldots ,c_k\in \mathbb {C}$
with
$c_1,\ldots ,c_k\in \mathbb {C}$
with
 $$ \begin{align*} \overline{M}_N \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
$$ \begin{align*} \overline{M}_N \bigg(\bigg|f - \sum_{j=1}^k c_{\xi_j} \xi_j\bigg|\bigg) < \varepsilon.\end{align*} $$
As usual it is also possible to characterize this by relative denseness of
![]() $\varepsilon $
-almost periods. More specifically, as discussed in [Reference Spindeler38] a measurable bounded
$\varepsilon $
-almost periods. More specifically, as discussed in [Reference Spindeler38] a measurable bounded
![]() $f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if and only if for each
$f : G\longrightarrow \mathbb {C}$
is Weyl almost periodic if and only if for each
![]() $\varepsilon>0$
there exists a relatively dense set
$\varepsilon>0$
there exists a relatively dense set
![]() $D\subset G$
and an
$D\subset G$
and an
![]() $N_0\in \mathbb {N}$
with
$N_0\in \mathbb {N}$
with
 $$ \begin{align*}\overline{M}_n \bigg(\bigg|f - f(\cdot - t)\bigg|\bigg) < \varepsilon\end{align*} $$
$$ \begin{align*}\overline{M}_n \bigg(\bigg|f - f(\cdot - t)\bigg|\bigg) < \varepsilon\end{align*} $$
for all
![]() $t\in D$
and
$t\in D$
and
![]() $n\geq N_0$
. By the preceding proposition, validity for all
$n\geq N_0$
. By the preceding proposition, validity for all
![]() $n\geq N_0$
can be replaced by validity for one n.
$n\geq N_0$
can be replaced by validity for one n.
Clearly, the set of Weyl almost periodic functions forms an algebra, is closed under uniform limits and under multiplication with Bohr almost periodic functions. Moreover, a crucial feature of Weyl mean almost periodic functions is uniform existence of means.
Lemma D.2. Let G be a locally compact abelian group and let
![]() $(B_n)$
be a Følner sequence on G. Let
$(B_n)$
be a Følner sequence on G. Let
![]() $f: G\longrightarrow \mathbb {C}$
be a bounded Weyl almost periodic function. Then, for any sequence
$f: G\longrightarrow \mathbb {C}$
be a bounded Weyl almost periodic function. Then, for any sequence
![]() $(r_n)$
in G the limit
$(r_n)$
in G the limit
 $$ \begin{align*} \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n + r_n} f(s)\,d s \end{align*} $$
$$ \begin{align*} \lim_{n\to \infty}\frac{1}{|B_n|} \int_{B_n + r_n} f(s)\,d s \end{align*} $$
exists and is independent of the sequence. In particular, the convergence is uniform in the chosen sequence.
The proof follows the same lines as the proof of the corresponding statement for Besicovitch almost periodic functions in the preceding section. For this reason, we leave it to the reader.