Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T04:11:42.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Properties of invariant measures in dynamical systems with the shadowing property

Published online by Cambridge University Press:  14 March 2017

JIAN LI Open the ORCID record for JIAN LI [Opens in a new window]  and
PIOTR OPROCHA
JIAN LI
Affiliation:
Department of Mathematics, Shantou University, Shantou, Guangdong 515063, PR China email [email protected]
PIOTR OPROCHA
Affiliation:
AGH University of Science and Technology, Faculty of Applied Mathematics, al. Mickiewicza 30, 30-059 Kraków, Poland National Supercomputing Centre IT4 Innovations, Division of the University of Ostrava, Institute for Research and Applications of Fuzzy Modeling, 30. dubna 22, 70103 Ostrava, Czech Republic email [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For dynamical systems with the shadowing property, we provide a method of approximation of invariant measures by ergodic measures supported on odometers and their almost one-to-one extensions. For a topologically transitive system with the shadowing property, we show that ergodic measures supported on odometers are dense in the space of invariant measures, and then ergodic measures are generic in the space of invariant measures. 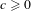We also show that for every $c\geq 0$ and 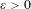$\unicode[STIX]{x1D700}>0$ the collection of ergodic measures (supported on almost one-to-one extensions of odometers) with entropy between $c$ and 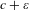$c+\unicode[STIX]{x1D700}$ is dense in the space of invariant measures with entropy at least $c$. Moreover, if in addition the entropy function is upper semi-continuous, then, for every 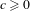$c\geq 0$, ergodic measures with entropy $c$ are generic in the space of invariant measures with entropy at least $c$.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 6 , September 2018 , pp. 2257 - 2294
Copyright
© Cambridge University Press, 2017 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aoki, N. and Hiraide, K.. Topological theory of dynamical systems. Recent Advances (North-Holland Mathematical Library, 52) . North-Holland Publishing, Amsterdam, 1994.Google Scholar
Bowen, R.. Periodic points and measures for Axiom A diffeomorphisms. Trans. Amer. Math. Soc. 154 (1971), 377–397.Google Scholar
Bowen, R.. Entropy-expansive maps. Trans. Amer. Math. Soc. 164 (1972), 323–331.Google Scholar
Bowen, R.. 𝜔-limit sets for Axiom A diffeomorphisms. J. Differential Equations 18 (1975), 333–339.Google Scholar
Brucks, K. M. and Bruin, H.. Topics from One-dimensional Dynamics (London Mathematical Society Student Texts, 62) . Cambridge University Press, Cambridge, 2004.Google Scholar
Comman, H.. Criteria for the density of the graph of the entropy map restricted to ergodic states. Ergod. Th. & Dynam. Sys. published online, doi:10.107/etds/2015.72.Google Scholar
Delahaye, J.-P.. Fonctions admettant des cycles d’ordre n’importe quelle puissance de 2 et aucun autre cycle. (French) [Functions admitting cycles of any power of 2 and no other cycle]. C. R. Acad. Sci. Paris Sér. A-B 291(4) (1980), A323–A325.Google Scholar
Denker, M., Grillenberger, C. and Sigmund, K.. Ergodic Theory on Compact Spaces (Lecture Notes in Mathematics, 527) . Springer, Berlin, 1976.Google Scholar
Downarowicz, T.. Survey of odometers and Toeplitz flows. Algebraic and Topological Dynamics (Contemporary Mathematics, 385) . American Mathematics Society, Providence, RI, 2005, p. 737.Google Scholar
Dudley, R.. Real Analysis and Probability (Cambridge Studies in Advanced Mathematics, 74) . Cambridge University Press, Cambridge, 2002.Google Scholar
Dong, Y., Oprocha, P. and Tian, X.. On the irregular points for systems with the shadowing property. Ergod. Th. & Dynam. Sys., to appear.Google Scholar
Eizenberg, A., Kifer, Y. and Weiss, B.. Large deviations for ℤ d -actions. Commun. Math. Phys. 164 (1994), 433–454.Google Scholar
Gurevič, B. M.. Topological entropy of a countable Markov chain. Dokl. Akad. Nauk SSSR 187 (1969), 715–718 (Russian); English trans. Soviet Math. Dokl. 10 (1969), 911–915.Google Scholar
Haraczyk, G., Kwietniak, D. and Oprocha, P.. Topological structure and entropy of mixing graph maps. Ergod. Th. & Dynam. Sys. 34 (2014), 1587–1614.Google Scholar
Israel, R. B. and Phelps, R. R.. Some convexity questions arising in statistical mechanics. Math. Scand. 54 (1984), 133–156.Google Scholar
Kitchens, B. P.. Symbolic dynamics. One-sided, Two-sided and Countable State Markov Shifts (Universitext) . Springer, Berlin, 1998.Google Scholar
Kuchta, M.. Shadowing property of continuous maps with zero topological entropy. Proc. Amer. Math. Soc. 119 (1993), 641–648.Google Scholar
Kurka, P.. Topological and symbolic dynamics. Cours Spécialisés [Specialized Courses]. 11 Société Mathématique de France, Paris, 2003.Google Scholar
Kwietniak, D., Łacka, M. and Oprocha, P.. A panorama of specification-like properties and their consequences. Dynamics and Numbers (Contemporary Mathematics, 669) . American Mathematical Society, Providence, RI, 2016, pp. 155–186.Google Scholar
Li, J. and Oprocha, P.. Shadowing property, weak mixing and regular recurrence. J. Dynam. Differential Equations 25 (2013), 1233–1249.Google Scholar
Lind, D. and Marcus, B.. An Introduction to Symbolic Dynamics and Coding. Cambridge University Press, Cambridge, 1995.Google Scholar
Misiurewicz, M.. Diffeomorphism without any measure with maximal entropy. Bull. Acad. Pol. Sci. 21 (1973), 903–910.Google Scholar
Moothathu, T. K. S.. Implications of pseudo-orbit tracing property for continuous maps on compacta. Topol. Appl. 158 (2011), 2232–2239.Google Scholar
Moothathu, T. K. S. and Oprocha, P.. Shadowing, entropy and minimal subsystems. Monatsh. Math. 172 (2013), 357–378.Google Scholar
Paul, M. E.. Construction of almost automorphic symbolic minimal flows. Gen. Topol. Appl. 6 (1976), 45–56.Google Scholar
Pfister, C.-E. and Sullivan, W. G.. Large deviations estimates for dynamical systems without the specification property. Applications to the 𝛽-shifts. Nonlinearity 18 (2005), 237–261.Google Scholar
Richeson, D. and Wiseman, J.. Chain recurrence rates and topological entropy. Topol. Appl. 156(2) (2008), 251–261.Google Scholar
Ruelle, D.. Statistical mechanics on a compact set with ℤ action satisfying expansiveness and specification. Trans. Amer. Math. Soc. 185 (1973), 237–251.Google Scholar
Ruette, S.. On the Vere-Jones classification and existence of maximal measures for countable topological Markov chains. Pacific J. Math. 209 (2003), 366–380.Google Scholar
Ruette, S.. Chaos on the interval — a survey of relationship between the various kinds of chaos for continuous interval maps. University Lecture Series, American Mathematical Society, to appear.Google Scholar
Salama, I. A.. On the recurrence of countable topological Markov chains. Symbolic Dynamics and Its Applications (New Haven, CT, 1991) (Contemporary Mathematics, 135) . American Mathematical Society, Providence, RI, 1992, pp. 349–360.Google Scholar
Sigmund, K.. Generic properties of invariant measures for Axiom A diffeomorphisms. Invent. Math. 11 (1970), 99–109.Google Scholar
Sigmund, K.. On dynamical systems with the specification property. Trans. Amer. Math. Soc. 190 (1974), 285–299.Google Scholar
Vere-Jones, D.. Geometric ergodicity in denumerable Markov chains. Quart. J. Math. Oxford Ser. 13 (1962), 7–28.Google Scholar
Walters, P.. On the pseudo-orbit tracing property and its relationship to stability. The Structure of Attractors in Dynamical Systems (Proc. Conf., North Dakota State University, Fargo, ND, 1977) (Lecture Notes in Mathematics, 668) . Springer, Berlin, 1978, pp. 231–244.Google Scholar
Walters, P.. An Introduction to Ergodic Theory. Springer, Berlin, 2001.Google Scholar
Williams, S.. Toeplitz minimal flows which are not uniquely ergodic. Z. Wahrsch. Verw. Gebiete 67 (1984), 95–107.Google Scholar
Coven, E. M., Kan, I. and Yorke, J. A.. Pseudo-orbit shadowing in the family of tent maps. Trans. Amer. Math. Soc. 308 (1988), 227–241.Google Scholar