Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-26T16:00:48.253Z Has data issue: false hasContentIssue false
  • English
  • Français

Pointwise multiple averages for sublinear functions

Part of: Classical measure theory Ergodic theory

Published online by Cambridge University Press:  05 November 2018

SEBASTIÁN DONOSO ,
ANDREAS KOUTSOGIANNIS  and
WENBO SUN
SEBASTIÁN DONOSO
Affiliation:
Instituto de Ciencias de la Ingeniería, Universidad de O’Higgins, Av. Libertador Bernardo O’Higgins 611, Rancagua, 2841959, Chile email [email protected]
ANDREAS KOUTSOGIANNIS
Affiliation:
Department of Mathematics,The Ohio State University, 231 West 18th Avenue, Columbus, OH 43210-1174, USA email [email protected], [email protected]
WENBO SUN
Affiliation:
Department of Mathematics,The Ohio State University, 231 West 18th Avenue, Columbus, OH 43210-1174, USA email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

For any measure-preserving system 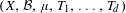$(X,{\mathcal{B}},\unicode[STIX]{x1D707},T_{1},\ldots ,T_{d})$ with no commutativity assumptions on the transformations 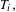$T_{i},$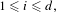$1\leq i\leq d,$ we study the pointwise convergence of multiple ergodic averages with iterates of different growth coming from a large class of sublinear functions. This class properly contains important subclasses of Hardy field functions of order zero and of Fejér functions, i.e., tempered functions of order zero. We show that the convergence of the single average, via an invariant property, implies the convergence of the multiple one. We also provide examples of sublinear functions which are, in general, bad for convergence on arbitrary systems, but good for uniquely ergodic systems. The case where the fastest function is linear is addressed as well, and we provide, in all the cases, an explicit formula of the limit function.

Keywords

pointwise convergencemultiple averagessublinear functionsFejér functionsHardy functions

MSC classification

Primary: 37A05: Measure-preserving transformations
Secondary: 37A30: Ergodic theorems, spectral theory, Markov operators 28A99: None of the above, but in this section
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 6 , June 2020 , pp. 1594 - 1618
Copyright
© Cambridge University Press, 2018

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Assani, I.. Multiple recurrence and almost sure convergence of weakly mixing dynamical systems. Israel J. Math. 103 (1998), 111–125.Google Scholar
Assani, I.. Pointwise convergence of nonconventional averages. Collect. Math. 102(2) (2005), 245–262.Google Scholar
Assani, I.. Averages along cubes for not necessarily commuting measure preserving transformations. Contemp. Math. 430 (2007), 1–19.Google Scholar
Assani, I.. Pointwise convergence of ergodic averages along cubes. J. Anal. Math. 110 (2010), 241–269.Google Scholar
Austin, T.. On the norm convergence of nonconventional ergodic averages. Ergod. Th. & Dynam. Sys. 30(2) (2010), 321–338.Google Scholar
Berend, D.. Joint ergodicity and mixing. J. Anal. Math. 45 (1985), 255–284.Google Scholar
Bergelson, V.. Weakly mixing PET. Ergod. Th. & Dynam. Sys. 7(3) (1987), 337–349.Google Scholar
Bergelson, V.. The Multifarious Poincaré Recurrence Theorem (Descriptive Set Theory and Dynamical Systems). Eds. Foreman, M., Kechris, A. S., Louveau, A. and Weiss, B.. Cambridge University Press, New York, 2000, pp. 31–57.Google Scholar
Bergelson, V. and Håland-Knutson, I.. Weakly mixing implies mixing of higher orders along tempered functions. Ergod. Th. & Dynam. Sys. 29(5) (2009), 1375–1416.Google Scholar
Bergelson, V. and Leibman, A.. A nilpotent Roth theorem. Invent. Math. 147 (2002), 429–470.Google Scholar
Boshernitzan, M., Kolesnik, G., Quass, A. and Weirdl, M.. Ergodic averaging sequences. J. Anal. Math. 95 (2005), 63–103.Google Scholar
Bourgain, J.. Pointwise ergodic theorems for arithmetic sets. Publ. Math. Inst. Hautes Études Sci. 69 (1989), 5–45.Google Scholar
Bourgain, J.. Double recurrence and almost sure convergence. J. Reine Angew. Math. 404 (1990), 140–161.Google Scholar
Chu, Q.. Convergence of multiple ergodic averages along cubes for several commuting transformations. Studia Math. 196(1) (2009), 13–22.Google Scholar
Chu, Q., Frantzikinakis, N. and Host, B.. Ergodic averages of commuting transformations with distinct degree polynomial iterates. Proc. Lond. Math. Soc. (3) 102 (2011), 801–842.Google Scholar
Chu, Q. and Frantzikinakis, N.. Pointwise convergence for cubic and polynomial ergodic averages of non-commuting transformations. Ergod. Th. & Dynam. Sys. 32(3) (2012), 877–897.Google Scholar
Donoso, S. and Sun, W.. A pointwise cubic average for two commuting transformations. Israel J. Math. 216(2) (2016), 657–678.Google Scholar
Donoso, S. and Sun, W.. Pointwise multiple averages for systems with two commuting transformations. Ergod. Th. & Dynam. Sys. 38(6) (2018), 2132–2157.Google Scholar
Donoso, S. and Sun, W.. Pointwise convergence of some multiple ergodic averages. Adv. Math. 330 (2018), 946–996.Google Scholar
Frantzikinakis, N.. Multiple recurrence and convergence for Hardy field sequences of polynomial growth. J. Anal. Math. 112 (2010), 79–135.Google Scholar
Frantzikinakis, N.. A multidimensional Szemeredi theorem for Hardy sequences of polynomial growth. Trans. Amer. Math. Soc. 367(8) (2015), 5653–5692.Google Scholar
Furstenberg, H.. Ergodic behavior of diagonal measures and a theorem of Szemerédi on arithmetic progressions. J. Anal. Math. 31 (1977), 204–256.Google Scholar
Gowers, W. T.. A new proof of Szemerédi’s theorem. Geom. Funct. Anal. 11 (2001), 465–588.Google Scholar
Gutman, Y., Huang, W., Shao, S. and Ye, X.. Almost sure convergence of the multiple ergodic average for certain weakly mixing systems. Acta Math. Sin. (Engl. Ser.) 34(1) (2018), 79–90.Google Scholar
Host, B.. Ergodic seminorms for commuting transformations and applications. Studia Math. 195(1) (2009), 31–49.Google Scholar
Host, B. and Kra, B.. Nonconventional averages and nilmanifolds. Ann. of Math. (2) 161(1) (2005), 398–488.Google Scholar
Huang, W., Shao, S. and Ye, X.. Pointwise convergence of multiple ergodic averages and strictly ergodic models. J. Anal. Math. (to appear). Preprint, 2014, arXiv:1406.5930.Google Scholar
Huang, W., Shao, S. and Ye, X.. Strictly ergodic models under face and parallelepiped group actions. Commun. Math. Stat. 5(1) (2017), 93–122.Google Scholar
Koutsogiannis, A.. Integer part polynomial correlation sequences. Ergod. Th. & Dynam. Sys. 38(4) (2018), 1525–1542.Google Scholar
Koutsogiannis, A.. Closest integer polynomial multiple recurrence along shifted primes. Ergod. Th. & Dynam. Sys. 38(2) (2018), 666–685.Google Scholar
Tao, T.. Norm convergence of multiple ergodic averages for commuting transformations. Ergod. Th. & Dynam. Sys. 28(2) (2008), 657–688.Google Scholar
Walsh, M.. Norm convergence of nilpotent ergodic averages. Ann. of Math. (2) 175(3) (2012), 1667–1688.Google Scholar