Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-26T18:12:41.201Z Has data issue: false hasContentIssue false
  • English
  • Français

A piecewise smooth Fermi–Ulam pingpong with potential

Part of: Ergodic theory Applications - Dynamical systems and ergodic theory Dynamical systems with hyperbolic behavior

Published online by Cambridge University Press:  04 March 2021

JING ZHOU Open the ORCID record for JING ZHOU [Opens in a new window]
JING ZHOU*
Affiliation:
Department of Mathematics, University of Maryland, College Park, MD20742, USA
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper we study a Fermi–Ulam model where a pingpong ball bounces elastically against a periodically oscillating platform in a gravity field. We assume that the platform motion 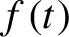$f(t)$ is 1-periodic and piecewise 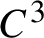$C^3$ with a singularity, 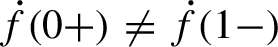$\dot {f}(0+)\ne \dot {f}(1-)$ . If the second derivative 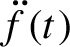$\ddot {f}(t)$ of the platform motion is either always positive or always less than 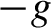$-g$ , where g is the gravitational constant, then the escaping orbits constitute a null set and the system is recurrent. However, under these assumptions, escaping orbits co-exist with bounded orbits at arbitrarily high energy levels.

Keywords

Fermi accelerationFermi–Ulamergodic theorybouncing ballescaping orbit

MSC classification

Primary: 37N05: Dynamical systems in classical and celestial mechanics 37D20: Uniformly hyperbolic systems (expanding, Anosov, Axiom A, etc.)
Secondary: 37A25: Ergodicity, mixing, rates of mixing 70F15: Celestial mechanics
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 5 , May 2022 , pp. 1847 - 1870
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anosov, D. V. and Sinai, Y. G.. Some smooth ergodic systems. Russian Math. Surveys 22(5) (1967), 103–167.CrossRefGoogle Scholar
Arnold, M. and Zharnitsky, V.. Pinball dynamics: unlimited energy growth in switching Hamiltonian systems. Comm. Math. Phys. 338(2) (2015), 501–521.CrossRefGoogle Scholar
Chen, J., Wang, F. and Zhang, H.-K.. Markov partition and thermodynamic formalism for hyperbolic systems with singularities. Preprint, 2019, arXiv:1709.00527.Google Scholar
Chernov, N.. Decay of correlations and dispersing billiards. J. Stat. Phys. 94(3–4) (1999), 513–556.CrossRefGoogle Scholar
Chernov, N. and Dolgopyat, D.. The Galton board: limit theorems and recurrence. J. Amer. Math. Soc. 22(3) (2009), 821–858.CrossRefGoogle Scholar
Chernov, N. and Zhang, H.-K.. On statistical properties of hyperbolic systems with singularities. J. Stat. Phys. 136(4) (2009), 615–642.CrossRefGoogle Scholar
de Simoi, J.. Stability and instability results in a model of Fermi acceleration. Discrete Contin. Dyn. Syst. 25(3) (2009), 719–750.CrossRefGoogle Scholar
de Simoi, J. and Dolgopyat, D.. Dynamics of some piecewise smooth Fermi–Ulam models. Chaos 22(2) (2012), 026124.CrossRefGoogle ScholarPubMed
de Simoi, J. and Toth, I. P.. An expansion estimate for dispersing planar billiards with corner points. Ann. Henri Poincaré 15(6) (2014), 1223–1243.CrossRefGoogle Scholar
Dolgopyat, D.. Lectures on bouncing balls. Online notes at http://www.users.math.umd.edu/∼dolgop/BBNotes.pdf.Google Scholar
Dolgopyat, D.. Bouncing balls in non-linear potentials. Discrete Contin. Dyn. Syst. 22(1–2) (2008), 165–182.CrossRefGoogle Scholar
Dolgopyat, D.. Fermi acceleration. Geometric and Probabilistic Structures in Dynamics (Contemporary Mathematics, 469). American Mathematical Society, Providence, RI, 2008, pp. 149–166.CrossRefGoogle Scholar
Dolgopyat, D. and Nándori, P.. Nonequilibrium density profiles in Lorentz tubes with thermostated boundaries. Comm. Pure Appl. Math. 69(4) (2016), 649–692.CrossRefGoogle Scholar
Dolgopyat, D. and Nándori, P.. Infinite measure mixing for some mechanical systems. Preprint, 2018, arXiv:1812.01174.Google Scholar
Fermi, E.. On the origin of the cosmic radiation. Phys. Rev. 75 (1949), 1169–1174.CrossRefGoogle Scholar
Gelfreich, V., Rom-Kedar, V. and Turaev, D.. Fermi acceleration and adiabatic invariants for non-autonomous billiards. Chaos 22(3) (2012), 033116, 21 pp.CrossRefGoogle ScholarPubMed
Laederich, S. and Levi, M.. Invariant curves and time-dependent potentials. Ergod. Th. & Dynam. Sys. 11(2) (1991), 365–378.CrossRefGoogle Scholar
Levi, M. and You, J.-G.. Oscillatory escape in a Duffing equation with a polynomial potential. J. Differential Equations 140(2) (1997), 415–426.CrossRefGoogle Scholar
Lichtenberg, A. J., Lieberman, M. A. and Cohen, R. H.. Fermi acceleration revisited. Physica D 1(3) (1980), 291–305.CrossRefGoogle Scholar
Liverani, C. and Wojtkowski, M.. Ergodicity in Hamiltonian systems. Dynamics Reported: Expositions in Dynamical Systems. Springer, Berlin, Heidelberg, 1995, pp. 130–202.CrossRefGoogle Scholar
Ortega, R.. Boundedness in a piecewise linear oscillator and a variant of the small twist theorem. Proc. Lond. Math. Soc. (3) 79(2) (1999), 381–413.CrossRefGoogle Scholar
Ortega, R.. Dynamics of a forced oscillator having an obstacle. Variational and Topological Methods in the Study of Nonlinear Phenomena (Pisa, 2000) (Progress in Nonlinear Differential Equations and Their Applications, 49). Birkhäuser, Boston, MA, 2002, pp. 75–87.Google Scholar
Pesin, Y. B.. Dynamical systems with generalized hyperbolic attractors: hyperbolic, ergodic and topological properties. Ergod. Th. & Dynam. Sys. 12(1) (1992), 123–151.CrossRefGoogle Scholar
Pustylnikov, L. D.. Stable and oscillating motions in nonautonomous dynamical systems. II. Tr. Mosk. Mat. Obš. 34 (1977), 3–103.Google Scholar
Pustylnikov, L. D.. On Ulam’s problem. Theoret. Math. Phys. 57 (1983), 1035–1038.CrossRefGoogle Scholar
Pustylnikov, L. D.. Existence of invariant curves for maps close to degenerate maps, and a solution of the Fermi–Ulam problem. Mat. Sb. 185 (1994), 113–124.Google Scholar
Sinai, Y. G.. Dynamical systems with elastic reflections. Russian Math. Surveys 25(2) (1970), 137–189.CrossRefGoogle Scholar
Ulam, S. M.. On some statistical properties of dynamical systems. Proceedings of the Fourth Berkeley Symposium on Mathematical Statistics and Probability (Contributions to Astronomy, Meteorology, and Physics, 3). University of California Press, Berkeley, CA, 1961, pp. 315–320.Google Scholar
Zharnitsky, V.. Instability in Fermi–Ulam ping-pong problem. Nonlinearity 11(6) (1998), 1481–1487.CrossRefGoogle Scholar