Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Arbieto, Alexander
Lopez Barragán, Andrés Mauricio
and
Morales Rojas, Carlos Arnoldo
2016.
Homoclinic classes for sectional-hyperbolic sets.
Kyoto Journal of Mathematics,
Vol. 56,
Issue. 3,
Catsigeras, Eleonora
and
Tian, Xueting
2016.
Dominated splitting, partial hyperbolicity and positive entropy.
Discrete and Continuous Dynamical Systems,
Vol. 36,
Issue. 9,
p.
4739.
Cao, Yongluo
and
Yang, Dawei
2016.
On Pesin's entropy formula for dominated splittings without mixed behavior.
Journal of Differential Equations,
Vol. 261,
Issue. 7,
p.
3964.
Santiago, Bruno
2018.
Dirac physical measures for generic diffeomorphisms.
Dynamical Systems,
Vol. 33,
Issue. 2,
p.
185.
Tian, Xueting
2018.
When a physical-like measure is physical or SRB?.
Journal of Differential Equations,
Vol. 265,
Issue. 8,
p.
3567.
Hua, Yongxia
Yang, Fan
and
Yang, Jiagang
2019.
A new criterion of physical measures for partially hyperbolic diffeomorphisms.
Transactions of the American Mathematical Society,
Vol. 373,
Issue. 1,
p.
385.
Catsigeras, Eleonora
and
Troubetzkoy, Serge
2019.
Invariant measures for typical continuous maps on manifolds.
Nonlinearity,
Vol. 32,
Issue. 10,
p.
3981.
Araujo, Vítor
and
Santos, Felipe
2019.
Pesin’s entropy formula for
$$C^1$$
C
1
non-uniformly expanding maps.
Mathematische Zeitschrift,
Vol. 291,
Issue. 3-4,
p.
1451.
Catsigeras, Eleonora
Tian, Xueting
and
Vargas, Edson
2019.
Topological entropy on points without physical-like behaviour.
Mathematische Zeitschrift,
Vol. 293,
Issue. 3-4,
p.
1043.
Burguet, David
2020.
Entropy of Physical Measures for $$C^\infty $$ Dynamical Systems.
Communications in Mathematical Physics,
Vol. 375,
Issue. 2,
p.
1201.
Crovisier, Sylvain
Yang, Dawei
and
Zhang, Jinhua
2020.
Empirical Measures of Partially Hyperbolic Attractors.
Communications in Mathematical Physics,
Vol. 375,
Issue. 1,
p.
725.
Gan, Shaobo
Yang, Fan
Yang, Jiagang
and
Zheng, Rusong
2021.
Statistical properties of physical-like measures*.
Nonlinearity,
Vol. 34,
Issue. 2,
p.
1014.
Yang, Jiagang
2021.
Entropy along expanding foliations.
Advances in Mathematics,
Vol. 389,
Issue. ,
p.
107893.
Tahzibi, Ali
2021.
Unstable entropy in smooth ergodic theory
*
.
Nonlinearity,
Vol. 34,
Issue. 8,
p.
R75.
Mi, Zeya
and
Cao, Yongluo
2021.
Statistical stability for diffeomorphisms with mostly expanding and mostly contracting centers.
Mathematische Zeitschrift,
Vol. 299,
Issue. 3-4,
p.
2519.
Sun, Peng
2022.
Non-dense orbits of systems with the approximate product property.
Nonlinearity,
Vol. 35,
Issue. 5,
p.
2682.
Guarino, Pablo
Guihéneuf, Pierre-Antoine
and
Santiago, Bruno
2022.
Dirac Physical Measures on Saddle-Type Fixed Points.
Journal of Dynamics and Differential Equations,
Vol. 34,
Issue. 2,
p.
983.
Liao, Gang
2022.
Lower bound in Pesin formula of C
1 interval maps*
.
Nonlinearity,
Vol. 35,
Issue. 3,
p.
1249.
Yang, Dawei
and
Zang, Yuntao
2023.
Volume growth and topological entropy of partially hyperbolic systems.
Israel Journal of Mathematics,
Vol. 255,
Issue. 1,
p.
325.
Yang, Jiagang
2023.
GEOMETRICAL AND MEASURE-THEORETIC STRUCTURES OF MAPS WITH A MOSTLY EXPANDING CENTER.
Journal of the Institute of Mathematics of Jussieu,
Vol. 22,
Issue. 2,
p.
919.
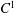 $C^1$ diffeomorphisms with dominated splitting
$C^1$ diffeomorphisms with dominated splitting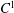 $C^1$ diffeomorphism with dominated splitting, we consider a non-empty set of invariant measures that describes the asymptotic statistics of Lebesgue-almost all orbits. They are the limits of convergent subsequences of averages of the Dirac delta measures supported on those orbits. We prove that the metric entropy of each of these measures is bounded from below by the sum of the Lyapunov exponents on the dominating sub-bundle. As a consequence, if those exponents are non-negative, and if the exponents on the dominated sub-bundle are non-positive, those measures satisfy the Pesin entropy formula.
$C^1$ diffeomorphism with dominated splitting, we consider a non-empty set of invariant measures that describes the asymptotic statistics of Lebesgue-almost all orbits. They are the limits of convergent subsequences of averages of the Dirac delta measures supported on those orbits. We prove that the metric entropy of each of these measures is bounded from below by the sum of the Lyapunov exponents on the dominating sub-bundle. As a consequence, if those exponents are non-negative, and if the exponents on the dominated sub-bundle are non-positive, those measures satisfy the Pesin entropy formula.

