Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T04:40:25.220Z Has data issue: false hasContentIssue false
  • English
  • Français

Partially hyperbolic diffeomorphisms and Lagrangian contact structures

Part of: Dynamical systems with hyperbolic behavior Global differential geometry

Published online by Cambridge University Press:  12 November 2021

MARTIN MION-MOUTON
MARTIN MION-MOUTON*
Affiliation:
IRMA, 7 rue René Descartes, 67084Strasbourg, France
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this paper, we classify the three-dimensional partially hyperbolic diffeomorphisms whose stable, unstable, and central distribution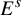s $E^s$ , 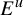$E^u$ , and 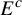$E^c$ are smooth, such that $E^s\oplus E^u$ is a contact distribution, and whose non-wandering set equals the whole manifold. We prove that up to a finite quotient or a finite power, they are smoothly conjugated either to a time-map of an algebraic contact-Anosov flow, or to an affine partially hyperbolic automorphism of a nil-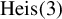 ${\mathrm {Heis}}{(3)}$ -manifold. The rigid geometric structure induced by the invariant distributions plays a fundamental part in the proof.

Keywords

partially hyperbolic diffeomorphismsrigid geometric structuresLagrangian contact structuresparabolic Cartan geometries

MSC classification

Primary: 37D30: Partially hyperbolic systems and dominated splittings
Secondary: 53C15: General geometric structures on manifolds (almost complex, almost product structures, etc.) 53C23: Global geometric and topological methods (à la Gromov); differential geometric analysis on metric spaces 53C30: Homogeneous manifolds 37D40: Dynamical systems of geometric origin and hyperbolicity (geodesic and horocycle flows, etc.)
Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 42 , Issue 8 , August 2022 , pp. 2583 - 2629
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bader, U., Frances, C. and Melnick, K.. An embedding theorem for automorphism groups of Cartan geometries. Geom. Funct. Anal. 19(2) (2009), 333–355.CrossRefGoogle Scholar
Barbot, T.. Three-dimensional Anosov flag manifolds. Geom. Topol. 14(1) (2010), 153–191.CrossRefGoogle Scholar
Benoist, Y., Foulon, P. and Labourie, F.. Flots d’Anosov à distributions stable et instable différentiables. J. Amer. Math. Soc. 5(1) (1992), 33–74.Google Scholar
Bonatti, C. and Zhang, J.. Transitive partially hyperbolic diffeomorphisms with one-dimensional neutral center. Sci. China Math. 63(9) (2020), 1647–1670.CrossRefGoogle Scholar
Brin, M. I.. Topological transitivity of one class of dynamic systems and flows of frames on manifolds of negative curvature. Funct. Anal. Appl. 9(1) (1975), 8–16.CrossRefGoogle Scholar
Čap, A. and Slovák, J.. Parabolic Geometries I: Background and General Theory (Mathematical Surveys and Monographs, 154). American Mathematical Society, Providence, RI, 2009.CrossRefGoogle Scholar
Carmo, M. D.. Differential Geometry of Curves and Surfaces. Prentice Hall, Englewood Cliffs, NJ, 1976.Google Scholar
Carrasco, P. D., Pujals, E. and Rodriguez-Hertz, F.. Classification of partially hyperbolic diffeomorphisms under some rigid conditions. Ergod. Th. & Dynam. Sys. doi:10.1017/etds.2020.85. Published online 26 May 2021.CrossRefGoogle Scholar
Crovisier, S. and Potrie, R.. Introduction to partially hyperbolic dynamics. Lecture Notes for a minicourse at ICTP, July 2015. Available at https://www.imo.universite-paris-saclay.fr/~crovisie/00-CP-Trieste-Version1.pdf.Google Scholar
Doubrov, B. and Komrakov, B.. The geometry of second-order ordinary differential equations. Preprint, 2016, arXiv:1602.00913 [math].Google Scholar
Frances, C.. Variations on Gromov’s open-dense orbit theorem. Bull. Soc. Math. France 146 (2016), 713–744.CrossRefGoogle Scholar
Fried, D. and Goldman, W. M.. Three-dimensional affine crystallographic groups. Adv. Math. 47(1) (1983), 1–49.CrossRefGoogle Scholar
Ghys, É.. Flots d’Anosov dont les feuilletages stables sont différentiables. Ann. Sci. Éc. Norm. Supér. 20(2) (1987), 251–270.CrossRefGoogle Scholar
Gromov, M.. Rigid transformations groups. Géométrie différentielle (Paris, 1986) (Travaux en cours, 33). Hermann, Paris, 1988, pp. 65–139.Google Scholar
Gromov, M. and D’Ambra, G.. Lectures on transformation groups: geometry and dynamics. Surv. Differ. Geom. 1 (1991), 19–111.Google Scholar
Hammerlindl, A. and Potrie, R.. Partial hyperbolicity and classification: a survey. Ergod. Th. & Dynam. Sys. 38(2) (2018), 401–443.CrossRefGoogle Scholar
Kanai, M.. Geodesic flows of negatively curved manifolds with smooth stable and unstable foliations. Ergod. Th. & Dynam. Sys. 8(2) (1988), 215–239.CrossRefGoogle Scholar
Kobayashi, S.. Transformation Groups in Differential Geometry (Classics in Mathematics, 70). Springer-Verlag, Berlin, 1995.Google Scholar
Kruglikov, B. and The, D.. The gap phenomenon in parabolic geometries. J. Reine Angew. Math. 2017(723) (2017), 153–215.CrossRefGoogle Scholar
Kulkarni, R. S. and Raymond, F.. 3-dimensional Lorentz space-forms and Seifert fiber spaces. J. Differential Geom. 21(2) (1985), 231–268.CrossRefGoogle Scholar
Lauret, J. and Will, C. E.. Nilmanifolds of dimension $\le 8$ admitting Anosov diffeomorphisms. Trans. Amer. Math. Soc. 361(5) (2009), 2377–2395.CrossRefGoogle Scholar
Mañé, R.. Quasi-Anosov diffeomorphisms and hyperbolic manifolds. Trans. Amer. Math. Soc. 229 (1977), 351–370.CrossRefGoogle Scholar
Mion-Mouton, M.. Quelques propriétés géométriques et dynamiques globales des structures Lagrangiennes de contact. Thèse, Université de Strasbourg, 2020, https://tel.archives-ouvertes.fr/tel-03013231/.Google Scholar
Pecastaing, V.. On two theorems about local automorphisms of geometric structures. Ann. Inst. Fourier 66(1) (2016), 175–208.CrossRefGoogle Scholar
Salein, F.. Variétés anti-de-Sitter de dimension 3. Thèse de doctorat, École normale supérieure de Lyon, 1999.CrossRefGoogle Scholar
Samuel, P.. Géométrie projective. Presses universitaires de France, Paris, 1989.Google Scholar
Sharpe, R. W.. Differential Geometry: Cartan’s Generalization of Klein’s Erlangen Program. Springer, Berlin, 1997, Foreword by S. S. Chern.Google Scholar
Smale, S.. Differentiable dynamical systems. Bull. Amer. Math. Soc. 73(6) (1967), 747–817.CrossRefGoogle Scholar
Sussmann, H. J.. Orbits of families of vector fields and integrability of distributions. Trans. Amer. Math. Soc. 180 (1973), 171–188.CrossRefGoogle Scholar
Tholozan, N.. Uniformisation des variétés pseudo-riemanniennes localement homogènes. Thèse de doctorat, Université Nice Sophia Antipolis, 2014.Google Scholar
Thurston, W. P.. Three-Dimensional Geometry and Topology. Vol. 1. Princeton University Press, Princeton, NJ, 1997.CrossRefGoogle Scholar
Tresse, A.. Détermination des invariants ponctuels de l’équation différentielle ordinaire du second ordre ${y}^{{\prime\prime} }=w\left(x,y,{y}^{\prime}\right)$ (Preisschriften gekrönt und hrsg. von der Fürstlich Jablonowskischen gesellschaft zu Leipzig. XXXII. Nr. XIII der mathematische-naturwissenschaftlichen section). S. Hirzel, Leipzig, 1896.Google Scholar
Zeghib, A.. Killing fields in compact Lorentz 3-manifolds. J. Differential Geom. 43(4) (1996), 859–894.CrossRefGoogle Scholar