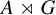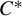1 Introduction
Partial dynamical systems have implicitly been used in mathematics long before the notion was formalized, at least since the study of differential equations. Indeed, the flow of a differentiable vector field can be naturally regarded as a partial action of the reals. More precisely, given a smooth vector field v on a manifold M, for
![]() $x\in M$
let
$x\in M$
let
![]() $\phi _x$
be the unique solution to the differential equation
$\phi _x$
be the unique solution to the differential equation
![]() $\phi '(t)=v(\phi (t))$
with initial condition
$\phi '(t)=v(\phi (t))$
with initial condition
![]() $\phi _x(0)=x$
, and let
$\phi _x(0)=x$
, and let
![]() $I_x\subseteq \mathbb {R}$
be the largest (open) neighbourhood of
$I_x\subseteq \mathbb {R}$
be the largest (open) neighbourhood of
![]() $0$
on which
$0$
on which
![]() $\phi _x$
is defined. For
$\phi _x$
is defined. For
![]() $t\in \mathbb {R}$
, set
$t\in \mathbb {R}$
, set
and let
![]() $\sigma _t\colon M_{-t}\to M_t$
be the diffeomorphism given by
$\sigma _t\colon M_{-t}\to M_t$
be the diffeomorphism given by
![]() $\sigma _t(x)=\phi _x(t)$
for all
$\sigma _t(x)=\phi _x(t)$
for all
![]() $x\in M_{-t}$
. The collection
$x\in M_{-t}$
. The collection
![]() $ \sigma =\{\sigma _t,M_t\colon t\in \mathbb {R}\}$
satisfies the crucial property that
$ \sigma =\{\sigma _t,M_t\colon t\in \mathbb {R}\}$
satisfies the crucial property that
![]() $\sigma _{s+t}$
extends
$\sigma _{s+t}$
extends
![]() $\sigma _s\circ \sigma _t$
, in the sense that whenever
$\sigma _s\circ \sigma _t$
, in the sense that whenever
![]() $x\in M_{-t}$
and
$x\in M_{-t}$
and
![]() $\sigma _t(x)$
belongs to
$\sigma _t(x)$
belongs to
![]() $M_{-s}$
, then x belongs to
$M_{-s}$
, then x belongs to
![]() $M_{-s-t}$
and
$M_{-s-t}$
and
![]() $\sigma _{s+t}(x)=\sigma _s(\sigma _t(x))$
. In modern language, this condition asserts that
$\sigma _{s+t}(x)=\sigma _s(\sigma _t(x))$
. In modern language, this condition asserts that
![]() $\sigma $
is a partial action of
$\sigma $
is a partial action of
![]() $\mathbb {R}$
on M.
$\mathbb {R}$
on M.
Partial actions were originally introduced by Exel and McClanahan in the 1990s, by isolating and abstracting the conditions observed in the context described above: a partial action of a discrete group G on a topological space X is a collection
![]() $\{X_g\colon g\in G\}$
of open sets of X and homeomorphisms
$\{X_g\colon g\in G\}$
of open sets of X and homeomorphisms
![]() $\sigma _g\colon X_{g^{-1}}\to X_g$
such that
$\sigma _g\colon X_{g^{-1}}\to X_g$
such that
![]() $\sigma _1={\mathrm {id}}_X$
and
$\sigma _1={\mathrm {id}}_X$
and
![]() $\sigma _{gh}$
extends
$\sigma _{gh}$
extends
![]() $\sigma _g\circ \sigma _h$
wherever the decomposition is well defined. The notion of a global (or ordinary) action is obtained by taking
$\sigma _g\circ \sigma _h$
wherever the decomposition is well defined. The notion of a global (or ordinary) action is obtained by taking
![]() $X_g=X$
for all
$X_g=X$
for all
![]() $g\in G$
. We refer the reader to a recent book [Reference Exel6] for a modern treatment of this topic and historical references. The study of partial actions (both on topological spaces and on
$g\in G$
. We refer the reader to a recent book [Reference Exel6] for a modern treatment of this topic and historical references. The study of partial actions (both on topological spaces and on
![]() $C^*$
-algebras) has been very fruitful, and has shed new light on the study of several objects. For example, the fact that the solutions of a differential equation on a compact manifold are defined on all
$C^*$
-algebras) has been very fruitful, and has shed new light on the study of several objects. For example, the fact that the solutions of a differential equation on a compact manifold are defined on all
![]() $\mathbb {R}$
can be easily proved in this more abstract setting; see Proposition 2.4 in [Reference Abadie1].
$\mathbb {R}$
can be easily proved in this more abstract setting; see Proposition 2.4 in [Reference Abadie1].
A typical example of a partial action is obtained by starting with a global action
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
, a not necessarily invariant ideal A in B, and setting
$\beta \colon G\to {\mathrm {Aut}}(B)$
, a not necessarily invariant ideal A in B, and setting
![]() $A_g=A\cap \beta _g(A)$
with
$A_g=A\cap \beta _g(A)$
with
![]() $\alpha _g=\beta _g|_{A_{g^{-1}}}$
for all
$\alpha _g=\beta _g|_{A_{g^{-1}}}$
for all
![]() $g\in G$
. Partial actions obtained in this way are called globalizable, and the globalization problem involves determining whether a given partial action is globalizable and, if it is, describing its globalization; see §3 of [Reference Abadie1]. As it turns out, not every partial action is globalizable (a necessary and sufficient condition is given in [Reference Ferraro7]). Even when a globalization exists, identifying it is often a challenging task, and its dynamical properties may differ significantly from those of
$g\in G$
. Partial actions obtained in this way are called globalizable, and the globalization problem involves determining whether a given partial action is globalizable and, if it is, describing its globalization; see §3 of [Reference Abadie1]. As it turns out, not every partial action is globalizable (a necessary and sufficient condition is given in [Reference Ferraro7]). Even when a globalization exists, identifying it is often a challenging task, and its dynamical properties may differ significantly from those of
![]() $\alpha $
.
$\alpha $
.
Given a partial group action
![]() $\alpha $
of a group G on a
$\alpha $
of a group G on a
![]() $C^*$
-algebra A, one can construct its crossed product
$C^*$
-algebra A, one can construct its crossed product
![]() $A\rtimes _\alpha G$
; see §I.8 in [Reference Exel6]. Large families of
$A\rtimes _\alpha G$
; see §I.8 in [Reference Exel6]. Large families of
![]() $C^*$
-algebras can be naturally described as partial crossed products, typically with commutative
$C^*$
-algebras can be naturally described as partial crossed products, typically with commutative
![]() $C^*$
-algebras, even in situations where similar descriptions do not exist for global crossed products. For example, every unital approximately finite-dimensional (AF)-algebra arises as the crossed product of a partial homeomorphism of a totally disconnected compact space, whereas no unital AF-algebra arises as the crossed product of a homeomorphism.
$C^*$
-algebras, even in situations where similar descriptions do not exist for global crossed products. For example, every unital approximately finite-dimensional (AF)-algebra arises as the crossed product of a partial homeomorphism of a totally disconnected compact space, whereas no unital AF-algebra arises as the crossed product of a homeomorphism.
It is therefore particularly important to develop tools to study partial crossed products. There have been a number of advances in this direction, for example, in reference to K-theory [Reference Exel5] and Takai duality [Reference Abadie1]. On the other hand, the study of partial actions of finite groups remains conspicuously underdeveloped. Indeed, and even in the globalizable case, virtually all averaging arguments (and their consequences) that are standard for global actions completely break down in this setting. The lack of approximate identities that are compatible with the partial action is also a source of difficulties in this setting. The goal of the present work is to make advances in the study of the structure of crossed products by partial actions of finite groups.
In the modern literature in
![]() $C^*$
-dynamical systems, several Rokhlin-type properties have an increasingly central role in the study of crossed products; see [Reference Gardella9, Reference Gardella and Hirshberg12, Reference Gardella and Santiago15, Reference Hirshberg, Winter and Zacharias18, Reference Izumi19, Reference Osaka and Phillips21, Reference Szabo, Wu and Zacharias23]. Their wide and fruitful applicability in the global setting make the extension of this theory to the partial setting worthy of exploration.
$C^*$
-dynamical systems, several Rokhlin-type properties have an increasingly central role in the study of crossed products; see [Reference Gardella9, Reference Gardella and Hirshberg12, Reference Gardella and Santiago15, Reference Hirshberg, Winter and Zacharias18, Reference Izumi19, Reference Osaka and Phillips21, Reference Szabo, Wu and Zacharias23]. Their wide and fruitful applicability in the global setting make the extension of this theory to the partial setting worthy of exploration.
Motivated by [Reference Hirshberg, Winter and Zacharias18], we define and study the notion of Rokhlin dimension in the partial setting; see Definition 2.1. The theory that we develop here exhibits phenomena that cannot be expected for global actions. Among others, the Rokhlin dimension of a globalizable partial action does not agree with that of its globalization; see Example 3.2. A notable exception is the unital case.
Theorem 1.1. (Theorem 3.4)
Let
![]() $\alpha $
be a globalizable partial action of a finite group on a unital
$\alpha $
be a globalizable partial action of a finite group on a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\beta $
be its globalization. Then
$\beta $
be its globalization. Then
Our original motivation was the study of the structure of the crossed product, particularly from the point of view of the classification programme for simple nuclear
![]() $C^*$
-algebras; see [Reference Elliott and Toms4]. As it turns out, this is technically much more complicated than in the global setting, and tackling this problem required us to first develop a decomposition theory for partial actions of finite groups into iterated extensions of relatively simpler systems; see [Reference Abadie, Gardella and Geffen2] and particularly §6 there. Here, we prove the following.
$C^*$
-algebras; see [Reference Elliott and Toms4]. As it turns out, this is technically much more complicated than in the global setting, and tackling this problem required us to first develop a decomposition theory for partial actions of finite groups into iterated extensions of relatively simpler systems; see [Reference Abadie, Gardella and Geffen2] and particularly §6 there. Here, we prove the following.
Theorem 1.2. (Theorem 4.7)
The following properties are inherited by crossed products or fixed point algebras by partial actions of finite groups with
![]() ${\mathrm {dim}_{\mathrm {Rok}}}<\infty $
.
${\mathrm {dim}_{\mathrm {Rok}}}<\infty $
.
-
(1) Having finite nuclear dimension or decomposition rank; for example,
 $$ \begin{align*} {\mathrm{dim}_{\mathrm{nuc}}}(A\rtimes_{\alpha} G)\leq (|G|-1)(\dim_{\mathrm{nuc}}(A)+1)(\dim_{\mathrm{Rok}}(\alpha)+1)+{\mathrm{dim}_{\mathrm{nuc}}}(A). \end{align*} $$
$$ \begin{align*} {\mathrm{dim}_{\mathrm{nuc}}}(A\rtimes_{\alpha} G)\leq (|G|-1)(\dim_{\mathrm{nuc}}(A)+1)(\dim_{\mathrm{Rok}}(\alpha)+1)+{\mathrm{dim}_{\mathrm{nuc}}}(A). \end{align*} $$
-
(2) When
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
, having finite stable/real rank; for example,
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
, having finite stable/real rank; for example,  $$ \begin{align*}\mathrm{sr}(A\rtimes_\alpha G)\leq \frac{|G|({\mathrm{sr}}(A)+{\mathrm{dim}_{\mathrm{Rok}}^{\mathrm{c}}}(\alpha)+3)-2}{2}. \end{align*} $$
$$ \begin{align*}\mathrm{sr}(A\rtimes_\alpha G)\leq \frac{|G|({\mathrm{sr}}(A)+{\mathrm{dim}_{\mathrm{Rok}}^{\mathrm{c}}}(\alpha)+3)-2}{2}. \end{align*} $$
-
(3) When
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
, absorbing a given strongly self-absorbing
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
, absorbing a given strongly self-absorbing
 $C^*$
-algebra.
$C^*$
-algebra.
(See [ Reference Geffen 16 ] for previously known results regarding nuclear dimension of C ⋆-algebras attached to partial dynamical systems.)
For unital partial actions, even more can be said; see Theorem 4.10. Most remarkably, the Universal Coefficient Theorem (UCT) is preserved in the commuting towers version. In this case, we also show that
![]() $A^\alpha $
is Morita equivalent to
$A^\alpha $
is Morita equivalent to
![]() $A\rtimes _\alpha G$
(see Theorem 4.9) a fact that rather surprisingly fails if unitality of A is dropped (see Example 4.8).
$A\rtimes _\alpha G$
(see Theorem 4.9) a fact that rather surprisingly fails if unitality of A is dropped (see Example 4.8).
Our structural results for crossed products are complemented by the fact that partial actions with finite Rokhlin dimension are relatively common. For example, we show that this notion is equivalent to freeness in the commutative setting.
Theorem 1.3. (Theorem 5.10)
Let
![]() $\sigma $
be a partial action of a finite group G on a locally compact Hausdorff space X with
$\sigma $
be a partial action of a finite group G on a locally compact Hausdorff space X with
![]() $\dim (X)<\infty $
. Then
$\dim (X)<\infty $
. Then
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\sigma )<\infty $
if and only if
${\mathrm {dim}_{\mathrm {Rok}}}(\sigma )<\infty $
if and only if
![]() $\sigma $
is free, in which case we have
$\sigma $
is free, in which case we have
The result in the global case is implicit [Reference Gardella10, Reference Hirshberg and Phillips17] and is an easy consequence of the existence of local cross-sections for the quotient map
![]() $\pi \colon X\to X/G$
. However, the proof in the partial setting is considerably more complicated, since for free partial actions there may not exist local cross-sections for
$\pi \colon X\to X/G$
. However, the proof in the partial setting is considerably more complicated, since for free partial actions there may not exist local cross-sections for
![]() $\pi $
. The proof in our context is quite involved and occupies most of §5. The main technical ingredient is the fact (Proposition 5.6) that an extension of topological partial actions with finite Rokhlin dimension again has finite Rokhlin dimension. Roughly speaking, one needs to lift Rokhlin towers from the quotient to the algebra, while at the same time respecting the domains of the partial action. The fact that the coefficient algebra is commutative seems to be crucial for this lifting problem to have a solution.
$\pi $
. The proof in our context is quite involved and occupies most of §5. The main technical ingredient is the fact (Proposition 5.6) that an extension of topological partial actions with finite Rokhlin dimension again has finite Rokhlin dimension. Roughly speaking, one needs to lift Rokhlin towers from the quotient to the algebra, while at the same time respecting the domains of the partial action. The fact that the coefficient algebra is commutative seems to be crucial for this lifting problem to have a solution.
2 Rokhlin dimension for partial actions of finite groups
In this section we define Rokhlin dimension for partial actions.
Definition 2.1. Let
![]() $\alpha =((A_g),(\alpha _g))_{g\in G}$
be a partial action of a finite group G on a
$\alpha =((A_g),(\alpha _g))_{g\in G}$
be a partial action of a finite group G on a
![]() $C^*$
-algebra A. For
$C^*$
-algebra A. For
![]() $d\in {\mathbb {N}}$
, we say that
$d\in {\mathbb {N}}$
, we say that
![]() $\alpha $
has Rokhlin dimension at most d, and write
$\alpha $
has Rokhlin dimension at most d, and write
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, if for every
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, if for every
![]() $\varepsilon>0$
and every finite subset
$\varepsilon>0$
and every finite subset
![]() $F\subseteq A$
, there exist positive contractions
$F\subseteq A$
, there exist positive contractions
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying:
$j=0,\ldots ,d$
, satisfying:
-
(1)
 $\|(\alpha _g(f_h^{(j)}x)-f_{gh}^{(j)}\alpha _g(x))a\|<\varepsilon $
for all
$\|(\alpha _g(f_h^{(j)}x)-f_{gh}^{(j)}\alpha _g(x))a\|<\varepsilon $
for all
 $g,h\in G$
,
$g,h\in G$
,
 $j=0,\ldots , d$
,
$j=0,\ldots , d$
,
 $a\in F$
and
$a\in F$
and
 $x\in A_{g^{-1}}\cap F$
;
$x\in A_{g^{-1}}\cap F$
; -
(2)
 $\|f_{g}^{(j)}f_{h}^{(j)}a\| < \varepsilon $
for
$\|f_{g}^{(j)}f_{h}^{(j)}a\| < \varepsilon $
for
 $j=0,\ldots ,d$
,
$j=0,\ldots ,d$
,
 $g,h \in G$
with
$g,h \in G$
with
 $g \neq h$
and
$g \neq h$
and
 $a\in F$
;
$a\in F$
; -
(3)
 $\|(\sum _{j=0}^{d}\sum _{g \in G} f_{g}^{(j)})a-a\|<\varepsilon $
for all
$\|(\sum _{j=0}^{d}\sum _{g \in G} f_{g}^{(j)})a-a\|<\varepsilon $
for all
 $a\in F$
;
$a\in F$
; -
(4)
 $\|(f_{g}^{(j)}b-bf_g^{(j)})a\| < \varepsilon $
for all
$\|(f_{g}^{(j)}b-bf_g^{(j)})a\| < \varepsilon $
for all
 $j =0,\ldots , d$
,
$j =0,\ldots , d$
,
 $g\in G$
, and
$g\in G$
, and
 $a,b\in F$
.
$a,b\in F$
.
Moreover, we say that
![]() $\alpha $
has Rokhlin dimension with commuting towers at most d, and write
$\alpha $
has Rokhlin dimension with commuting towers at most d, and write
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
, if for every
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
, if for every
![]() $\varepsilon>0$
and every finite subset
$\varepsilon>0$
and every finite subset
![]() $F\subseteq A$
, there exist positive contractions
$F\subseteq A$
, there exist positive contractions
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying conditions (1)–(4) above, in addition to:
$j=0,\ldots ,d$
, satisfying conditions (1)–(4) above, in addition to:
-
(5)
 $\|(f_{g}^{(j)}f_{h}^{(k)}-f_{h}^{(k)}f_{g}^{(j)})a\| < \varepsilon $
for all
$\|(f_{g}^{(j)}f_{h}^{(k)}-f_{h}^{(k)}f_{g}^{(j)})a\| < \varepsilon $
for all
 $j,k =0,\ldots , d$
,
$j,k =0,\ldots , d$
,
 $g,h\in G$
and
$g,h\in G$
and
 $a\in F$
.
$a\in F$
.
In either case, we call the elements
![]() $f_g^{(j)}$
above Rokhlin towers for
$f_g^{(j)}$
above Rokhlin towers for
![]() $(F,\varepsilon )$
.
$(F,\varepsilon )$
.
We define the Rokhlin dimension of
![]() $\alpha $
by
$\alpha $
by
and define the Rokhlin dimension with commuting towers
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )$
similarly.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )$
similarly.
The multiplicative witness
![]() $a\in F$
that appears in conditions (1)–(5) also appears in the definition of Rokhlin dimension for global actions setting [Reference Hirshberg and Phillips17], and it can be omitted when A is unital. On the other hand, the witness
$a\in F$
that appears in conditions (1)–(5) also appears in the definition of Rokhlin dimension for global actions setting [Reference Hirshberg and Phillips17], and it can be omitted when A is unital. On the other hand, the witness
![]() $x\in F\cap A_{g^{-1}}$
is a conceptually new condition that cannot be omitted even if A is unital.
$x\in F\cap A_{g^{-1}}$
is a conceptually new condition that cannot be omitted even if A is unital.
In the early stages of this project, it was unclear whether one should not instead require the stronger condition
![]() $\|\alpha _g(f_h^{(j)}x)-f_{gh}^{(j)}\alpha _g(x)\|<\varepsilon \|x\|$
for all
$\|\alpha _g(f_h^{(j)}x)-f_{gh}^{(j)}\alpha _g(x)\|<\varepsilon \|x\|$
for all
![]() $g,h\in G$
,
$g,h\in G$
,
![]() $j=0,\ldots ,d$
, and all
$j=0,\ldots ,d$
, and all
![]() $x\in A_{g^{-1}}$
. As it turns out, the stronger condition implies that the given partial action is in fact globalizable, which suggests that it was not the right notion to consider.
$x\in A_{g^{-1}}$
. As it turns out, the stronger condition implies that the given partial action is in fact globalizable, which suggests that it was not the right notion to consider.
Unlike the case of global actions, the different elements within one tower are not ‘interchangeable’, as they tend to have different ‘sizes’. In fact, the positive contraction corresponding to the unit of the group is usually much larger than the others. The following is an extreme example of this situation.
Example 2.2. Let G be a finite group, and let A be a unital
![]() $C^*$
-algebra. We define the trivial partial action of G on A by setting
$C^*$
-algebra. We define the trivial partial action of G on A by setting
![]() $A_g=\{0\}$
for
$A_g=\{0\}$
for
![]() $g\in G\setminus \{1\}$
. This partial action has Rokhlin dimension zero, with Rokhlin towers given by
$g\in G\setminus \{1\}$
. This partial action has Rokhlin dimension zero, with Rokhlin towers given by
![]() $f_1=1_A$
and
$f_1=1_A$
and
![]() $f_g=0$
for
$f_g=0$
for
![]() $g\in G\setminus \{1\}$
. Note that
$g\in G\setminus \{1\}$
. Note that
![]() $A\rtimes _\alpha G=A$
. Moreover, this is the only partial action of G on A with the 1-decomposition property (Definition 4.2); see Example 2.6 in [Reference Abadie, Gardella and Geffen2].
$A\rtimes _\alpha G=A$
. Moreover, this is the only partial action of G on A with the 1-decomposition property (Definition 4.2); see Example 2.6 in [Reference Abadie, Gardella and Geffen2].
Next, we show that condition (1) in Definition 2.1 can be strengthened in the case of unital partial actions (that is, partial actions whose domains are unital).
Remark 2.3. Let
![]() $\alpha $
be a unital partial action of a finite group G on a
$\alpha $
be a unital partial action of a finite group G on a
![]() $C^*$
-algebra A, with units
$C^*$
-algebra A, with units
![]() $1_g\in A_g$
, for
$1_g\in A_g$
, for
![]() $g\in G$
. Then
$g\in G$
. Then
![]() $1_{gh}1_g=\alpha _g(1_h1_{g^{-1}})$
for all
$1_{gh}1_g=\alpha _g(1_h1_{g^{-1}})$
for all
![]() $g,h\in G$
.
$g,h\in G$
.
Proposition 2.4. Adopt the notation from Definition 2.1, and suppose that
![]() $\alpha $
is a unital partial action. For
$\alpha $
is a unital partial action. For
![]() $g\in G$
, denote by
$g\in G$
, denote by
![]() $1_g$
the unit of
$1_g$
the unit of
![]() $A_g$
. Then condition (1) in Definition 2.1 can be replaced by:
$A_g$
. Then condition (1) in Definition 2.1 can be replaced by:
-
(1’)
 $\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_g$
for all
$\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_g$
for all
 $g,h\in G$
, and for all
$g,h\in G$
, and for all
 $j=0,\ldots , d$
.
$j=0,\ldots , d$
.
Proof We prove the proposition for
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
, since the proof for
${\mathrm {dim}_{\mathrm {Rok}}}$
, since the proof for
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is analogous. Using the identity
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is analogous. Using the identity
![]() $x=x1_{g^{-1}}$
for all
$x=x1_{g^{-1}}$
for all
![]() $x\in A_{g^{-1}}$
and
$x\in A_{g^{-1}}$
and
![]() $g\in G$
, one easily shows that (1’) implies the following identity for all
$g\in G$
, one easily shows that (1’) implies the following identity for all
![]() $g,h\in G$
,
$g,h\in G$
,
![]() $j=0,\ldots ,d$
, and all
$j=0,\ldots ,d$
, and all
![]() $x\in A_{g^{-1}}$
:
$x\in A_{g^{-1}}$
:
This identity clearly implies (1). Conversely, let
![]() $\varepsilon>0$
and a finite subset
$\varepsilon>0$
and a finite subset
![]() $F \subseteq A$
be given. Without loss of generality, we assume that F consists of contractions and that
$F \subseteq A$
be given. Without loss of generality, we assume that F consists of contractions and that
![]() $\{1_g\colon g\in G\}\subseteq F$
. Set
$\{1_g\colon g\in G\}\subseteq F$
. Set
![]() $\varepsilon _0={\varepsilon }/({|G|(d+1)+1})$
and find Rokhlin towers
$\varepsilon _0={\varepsilon }/({|G|(d+1)+1})$
and find Rokhlin towers
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying conditions (1), (2), (3), and (4) in Definition 2.1 for
$j=0,\ldots ,d$
, satisfying conditions (1), (2), (3), and (4) in Definition 2.1 for
![]() $(F,\varepsilon _0)$
. Define positive contractions
$(F,\varepsilon _0)$
. Define positive contractions
![]() $\widetilde {f}_g^{(j)}\in A_g$
, for all
$\widetilde {f}_g^{(j)}\in A_g$
, for all
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, by
$j=0,\ldots ,d$
, by
![]() $\widetilde {f}_g^{(j)}=\alpha _g(f_1^{(j)}1_{g^{-1}})$
. Since
$\widetilde {f}_g^{(j)}=\alpha _g(f_1^{(j)}1_{g^{-1}})$
. Since
![]() $1_{g^{-1}}$
belongs to F, condition (1) for
$1_{g^{-1}}$
belongs to F, condition (1) for
![]() $f_1^{(j)}$
gives
$f_1^{(j)}$
gives
for all
![]() $g\in G$
and all
$g\in G$
and all
![]() $j=0,\ldots ,d$
. We claim that these elements satisfy the conditions in Definition 2.1 with (1) replaced by (1’).
$j=0,\ldots ,d$
. We claim that these elements satisfy the conditions in Definition 2.1 with (1) replaced by (1’).
We begin with (1’). For
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j=0,\ldots ,d$
, we have
$j=0,\ldots ,d$
, we have
 $$ \begin{align*} \alpha_g(\widetilde{f}_h^{(j)}1_{g^{-1}})&=\alpha_g(\alpha_h(f_1^{(j)}1_{h^{-1}})1_{g^{-1}})\\ &=\alpha_g(\alpha_h(f_1^{(j)}1_{h^{-1}}1_{{(gh)}^{-1}}))\\ &=\alpha_{gh}(f_1^{(j)}1_{{(gh)}^{-1}})1_g =\widetilde{f}_{gh}^{(j)}1_g. \end{align*} $$
$$ \begin{align*} \alpha_g(\widetilde{f}_h^{(j)}1_{g^{-1}})&=\alpha_g(\alpha_h(f_1^{(j)}1_{h^{-1}})1_{g^{-1}})\\ &=\alpha_g(\alpha_h(f_1^{(j)}1_{h^{-1}}1_{{(gh)}^{-1}}))\\ &=\alpha_{gh}(f_1^{(j)}1_{{(gh)}^{-1}})1_g =\widetilde{f}_{gh}^{(j)}1_g. \end{align*} $$
Finally, conditions (2), (3) and (4) for the
![]() $\widetilde {f}_g^{(j)}$
follow by combining (2.1) with conditions (2), (3) and (4) for
$\widetilde {f}_g^{(j)}$
follow by combining (2.1) with conditions (2), (3) and (4) for
![]() $f_g^{(j)}$
. We omit the details.
$f_g^{(j)}$
. We omit the details.
Remark 2.5. In the context of Proposition 2.4, one can show that condition (2) can be replaced by:
-
(2’)
 $f_g^{(j)}f_h^{(j)}=0$
for all
$f_g^{(j)}f_h^{(j)}=0$
for all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
and for all
$g\neq h$
and for all
 $j=0,\ldots ,d$
.
$j=0,\ldots ,d$
.
Since we do not need this, we omit its proof. We stress the fact that it is in general not possible to replace (1) and (2) simultaneously with (1’) and (2’), since the argument used to get (1’) from (1) does not preserve (2’), and vice versa.
We close this section by proving that the finite Rokhlin dimension behaves well with respect to restriction to invariant ideals and passage to equivariant quotients.
Proposition 2.6. Let A be a
![]() $C^*$
-algebra, let G be a finite group, and let
$C^*$
-algebra, let G be a finite group, and let
![]() $\alpha $
be a partial action of G on A. Let I be a G-invariant ideal of A. We denote by
$\alpha $
be a partial action of G on A. Let I be a G-invariant ideal of A. We denote by
![]() $\alpha |_{I}$
and
$\alpha |_{I}$
and
![]() $\overline {\alpha }$
the induced partial actions of G on I and
$\overline {\alpha }$
the induced partial actions of G on I and
![]() $A/I$
, respectively. Then
$A/I$
, respectively. Then
Similar estimates hold for
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
.
Proof We prove the results for
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
, s ince the case of
${\mathrm {dim}_{\mathrm {Rok}}}$
, s ince the case of
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is similar. We assume from now on that
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is similar. We assume from now on that
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
, otherwise there is nothing to prove.
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
, otherwise there is nothing to prove.
We prove
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{I})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
first. Let
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{I})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
first. Let
![]() $\varepsilon>0$
and let a finite subset
$\varepsilon>0$
and let a finite subset
![]() $F\subseteq I$
be given. Without loss of generality, we assume that F contains only contractions. Set
$F\subseteq I$
be given. Without loss of generality, we assume that F contains only contractions. Set
![]() $\varepsilon _0={\varepsilon }/({5|G|(d+1)+2})$
. Apply Definition 2.1 to find Rokhlin towers
$\varepsilon _0={\varepsilon }/({5|G|(d+1)+2})$
. Apply Definition 2.1 to find Rokhlin towers
![]() $f_g^{(j)}\in A_g$
with
$f_g^{(j)}\in A_g$
with
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, for
$j=0,\ldots ,d$
, for
![]() $(F, \varepsilon _0)$
. By making a small renormalization, we may assume that
$(F, \varepsilon _0)$
. By making a small renormalization, we may assume that
![]() $\sum _{g\in G}\sum _{j=0}^df_g^{(j)}$
is a contraction. By considering an approximate identity of I which is quasi-central in A, find
$\sum _{g\in G}\sum _{j=0}^df_g^{(j)}$
is a contraction. By considering an approximate identity of I which is quasi-central in A, find
![]() $e\in I$
satisfying
$e\in I$
satisfying
for all
![]() $g\in G$
, all
$g\in G$
, all
![]() $j=0,\ldots ,d$
, and all
$j=0,\ldots ,d$
, and all
![]() $b\in \bigcup \nolimits _{g\in G}\alpha _g(F\cap A_{g^{-1}}).$
$b\in \bigcup \nolimits _{g\in G}\alpha _g(F\cap A_{g^{-1}}).$
For
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, set
$j=0,\ldots ,d$
, set
![]() $\widetilde {f}_g^{(j)}=e^{{1}/{2}}f_g^{(j)}e^{{1}/{2}}$
. We claim that
$\widetilde {f}_g^{(j)}=e^{{1}/{2}}f_g^{(j)}e^{{1}/{2}}$
. We claim that
![]() $\{\widetilde {f}_g^{(j)}\colon g\in G, j=0,\ldots ,d\}$
are Rokhlin towers with respect to
$\{\widetilde {f}_g^{(j)}\colon g\in G, j=0,\ldots ,d\}$
are Rokhlin towers with respect to
![]() $(F, \varepsilon )$
for
$(F, \varepsilon )$
for
![]() $\alpha |_I$
. Note that
$\alpha |_I$
. Note that
![]() $\widetilde {f}_g^{(j)}$
belongs to
$\widetilde {f}_g^{(j)}$
belongs to
![]() $A_g\cap I=I_g$
. In order to check (1), let
$A_g\cap I=I_g$
. In order to check (1), let
![]() $g\in G$
, let
$g\in G$
, let
![]() $x\in F\cap I_{g^{-1}}=F\cap A_{g^{-1}}$
, let
$x\in F\cap I_{g^{-1}}=F\cap A_{g^{-1}}$
, let
![]() $a\in F$
, and let
$a\in F$
, and let
![]() $j=0,\ldots ,d$
. Then
$j=0,\ldots ,d$
. Then
 $$ \begin{align*} \alpha_g(\widetilde{f}_h^{(j)}x)a&= \alpha_g(e^{{1}/{2}}f_h^{(j)}e^{{1}/{2}}x)a \approx_{\varepsilon_0} \alpha_g(f_h^{(j)}ex)a\\ &\approx_{\varepsilon_0} \alpha_g(f_h^{(j)}x)a \approx_{\varepsilon_0} f_{gh}^{(j)}\alpha_g(x)a\\ &\approx_{\varepsilon_0} f_{gh}^{(j)}e\alpha_g(x)a \approx_{\varepsilon_0} e^{{1}/{2}}f_{gh}^{(j)}e^{{1}/{2}}\alpha_g(x)a = \widetilde{f}_{gh}^{(j)}\alpha_g(x)a. \end{align*} $$
$$ \begin{align*} \alpha_g(\widetilde{f}_h^{(j)}x)a&= \alpha_g(e^{{1}/{2}}f_h^{(j)}e^{{1}/{2}}x)a \approx_{\varepsilon_0} \alpha_g(f_h^{(j)}ex)a\\ &\approx_{\varepsilon_0} \alpha_g(f_h^{(j)}x)a \approx_{\varepsilon_0} f_{gh}^{(j)}\alpha_g(x)a\\ &\approx_{\varepsilon_0} f_{gh}^{(j)}e\alpha_g(x)a \approx_{\varepsilon_0} e^{{1}/{2}}f_{gh}^{(j)}e^{{1}/{2}}\alpha_g(x)a = \widetilde{f}_{gh}^{(j)}\alpha_g(x)a. \end{align*} $$
Thus
![]() $\|\alpha _g(\widetilde {f}_h^{(j)}x)a- \widetilde {f}_{gh}^{(j)}\alpha _g(x)a\|< 5\varepsilon _0<\varepsilon $
, as desired. Condition (2) is easily checked and is left to the reader. For (3), let
$\|\alpha _g(\widetilde {f}_h^{(j)}x)a- \widetilde {f}_{gh}^{(j)}\alpha _g(x)a\|< 5\varepsilon _0<\varepsilon $
, as desired. Condition (2) is easily checked and is left to the reader. For (3), let
![]() $a\in F$
be given. Then
$a\in F$
be given. Then
 $$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G} \widetilde{f}_g^{(j)}a &=\sum\limits_{j=0}^{d} \sum\limits_{g\in G} e^{{1}/{2}}f_g^{(j)}e^{{1}/{2}}a\\ &\approx_{|G|(d+1)\varepsilon_0} \sum\limits_{j=0}^{d} \sum\limits_{g\in G} f_g^{(j)}ea\\ &\approx_{\varepsilon_0} \sum\limits_{j=0}^{d} \sum\limits_{g\in G} f_g^{(j)}a\approx_{\varepsilon_0}a, \end{align*} $$
$$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G} \widetilde{f}_g^{(j)}a &=\sum\limits_{j=0}^{d} \sum\limits_{g\in G} e^{{1}/{2}}f_g^{(j)}e^{{1}/{2}}a\\ &\approx_{|G|(d+1)\varepsilon_0} \sum\limits_{j=0}^{d} \sum\limits_{g\in G} f_g^{(j)}ea\\ &\approx_{\varepsilon_0} \sum\limits_{j=0}^{d} \sum\limits_{g\in G} f_g^{(j)}a\approx_{\varepsilon_0}a, \end{align*} $$
where in the second-to-last step we use the fact that
![]() $\sum _{g\in G}\sum _{j=0}^df_g^{(j)}$
is a contraction. Finally, to check (4), let
$\sum _{g\in G}\sum _{j=0}^df_g^{(j)}$
is a contraction. Finally, to check (4), let
![]() $g\in G, j=0,\ldots ,d$
, and
$g\in G, j=0,\ldots ,d$
, and
![]() $a\in F$
. Then
$a\in F$
. Then
We turn to the inequality
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })\leq d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
. Write
${\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })\leq d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
. Write
![]() $\pi \colon A\to A/I$
for the canonical equivariant map. Let
$\pi \colon A\to A/I$
for the canonical equivariant map. Let
![]() $\overline {F}\subseteq A/I$
be a finite set and let
$\overline {F}\subseteq A/I$
be a finite set and let
![]() $\varepsilon>0$
. Let
$\varepsilon>0$
. Let
![]() $F\subseteq A$
be any finite set satisfying
$F\subseteq A$
be any finite set satisfying
![]() $\pi (F)=\overline {F}$
, and apply Definition 2.1 for
$\pi (F)=\overline {F}$
, and apply Definition 2.1 for
![]() $\alpha $
to find Rokhlin towers
$\alpha $
to find Rokhlin towers
![]() $f_g^{(j)}\in A_g$
, with
$f_g^{(j)}\in A_g$
, with
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, for
$j=0,\ldots ,d$
, for
![]() $(F,\varepsilon )$
. It is then immediate that the positive contractions
$(F,\varepsilon )$
. It is then immediate that the positive contractions
![]() $\overline {f}_g^{(j)}=\pi (f_g^{(j)})$
witness the fact that
$\overline {f}_g^{(j)}=\pi (f_g^{(j)})$
witness the fact that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })\leq d$
, as desired.
${\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })\leq d$
, as desired.
3 Rokhlin dimension and globalization
The basic example of a partial action is obtained by starting with a global action
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
and a (not necessarily invariant) ideal A in B, and then setting
$\beta \colon G\to {\mathrm {Aut}}(B)$
and a (not necessarily invariant) ideal A in B, and then setting
![]() $A_g=A\cap \beta _g(A)$
and
$A_g=A\cap \beta _g(A)$
and
![]() $\alpha _g=\beta _g|_{A_{g^{-1}}}$
for all
$\alpha _g=\beta _g|_{A_{g^{-1}}}$
for all
![]() $g\in G$
. Actions of this form are called globalizable, since they are induced by a global action. Here is the precise definition.
$g\in G$
. Actions of this form are called globalizable, since they are induced by a global action. Here is the precise definition.
Definition 3.1. Let G be a finite group, let A be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha $
be a partial action of G on A. A triple
$\alpha $
be a partial action of G on A. A triple
![]() $(B,\beta ,\iota )$
consisting of a
$(B,\beta ,\iota )$
consisting of a
![]() $C^*$
-algebra B, a global action
$C^*$
-algebra B, a global action
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
, and an embedding
$\beta \colon G\to {\mathrm {Aut}}(B)$
, and an embedding
![]() $\iota \colon A\to B$
is said to be an enveloping action for
$\iota \colon A\to B$
is said to be an enveloping action for
![]() $\alpha $
if the following conditions are satisfied:
$\alpha $
if the following conditions are satisfied:
-
(a) A (identified with
 $\iota (A)$
) is an ideal in B;
$\iota (A)$
) is an ideal in B; -
(b)
 $A_g=A\cap \beta _g(A)$
for all
$A_g=A\cap \beta _g(A)$
for all
 $g\in G$
;
$g\in G$
; -
(c)
 $\alpha _g(a)=\beta _g(a)$
for all
$\alpha _g(a)=\beta _g(a)$
for all
 $a\in A_{g^{-1}}$
and all
$a\in A_{g^{-1}}$
and all
 $g\in G$
;
$g\in G$
; -
(d)
 $B=\overline {\mathrm {span}}\{\beta _g(a)\colon a\in A, g\in G \}$
.
$B=\overline {\mathrm {span}}\{\beta _g(a)\colon a\in A, g\in G \}$
.
(If such a dynamical system
![]() $(B,\beta )$
exists, then it is unique up to an equivariant isomorphism extending the identity on A by Theorem 3.8 in [Reference Abadie1].) We say that
$(B,\beta )$
exists, then it is unique up to an equivariant isomorphism extending the identity on A by Theorem 3.8 in [Reference Abadie1].) We say that
![]() $\alpha $
is globalizable if it has an enveloping action.
$\alpha $
is globalizable if it has an enveloping action.
Not every partial action is globalizable, and even when it is, identifying its enveloping action may turn out to be challenging. Since there is a vast amount of literature concerning global actions with finite Rokhlin dimension, it would be very useful if one could relate the Rokhlin dimension of a (globalizable) partial action to its globalization. Unfortunately, these values do not necessarily agree.
Example 3.2. Set
![]() $X=S^1\setminus \{1\}$
and
$X=S^1\setminus \{1\}$
and
![]() $U=X\setminus \{-1\}$
. Let
$U=X\setminus \{-1\}$
. Let
![]() $\sigma \in \mathrm {Homeo}(U)$
be given by
$\sigma \in \mathrm {Homeo}(U)$
be given by
![]() $\sigma (x)=-x$
for all
$\sigma (x)=-x$
for all
![]() $x\in U$
. Denote by
$x\in U$
. Denote by
![]() $\gamma $
the partial action of
$\gamma $
the partial action of
![]() ${\mathbb {Z}}_2=\{-1,1\}$
on
${\mathbb {Z}}_2=\{-1,1\}$
on
![]() $C_0(X)$
determined by
$C_0(X)$
determined by
![]() $\sigma $
. Then
$\sigma $
. Then
![]() $\gamma $
is globalizable, with globalization
$\gamma $
is globalizable, with globalization
![]() $\widetilde {\gamma }\colon {\mathbb {Z}}_2\to {\mathrm {Aut}}(C(S^1))$
induced by multiplication by
$\widetilde {\gamma }\colon {\mathbb {Z}}_2\to {\mathrm {Aut}}(C(S^1))$
induced by multiplication by
![]() $-1$
.
$-1$
.
Let
![]() $\delta \colon {\mathbb {Z}}_2\to {\mathrm {Aut}}({\mathbb {C}}\oplus {\mathbb {C}})$
be the flip action. Set
$\delta \colon {\mathbb {Z}}_2\to {\mathrm {Aut}}({\mathbb {C}}\oplus {\mathbb {C}})$
be the flip action. Set
![]() $\alpha =\gamma \otimes \delta $
, which is globalizable with globalization given by
$\alpha =\gamma \otimes \delta $
, which is globalizable with globalization given by
![]() $(B,\beta )=(C(S^1)\oplus C(S^1),\widetilde {\gamma }\otimes \delta )$
. It is clear that
$(B,\beta )=(C(S^1)\oplus C(S^1),\widetilde {\gamma }\otimes \delta )$
. It is clear that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )=0$
, since we may take
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )=0$
, since we may take
![]() $p_{-1}=(1,0)$
and
$p_{-1}=(1,0)$
and
![]() $p_1=(0,1)$
in B.
$p_1=(0,1)$
in B.
We claim that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\neq 0$
. From now on, we identify X with
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\neq 0$
. From now on, we identify X with
![]() $(0,2)$
and U with
$(0,2)$
and U with
![]() $(0,1)\cup (1,2)$
. Arguing by contradiction, set
$(0,1)\cup (1,2)$
. Arguing by contradiction, set
![]() $\varepsilon =3/16$
and take
$\varepsilon =3/16$
and take
![]() $I_{1}=[\varepsilon ,2-\varepsilon ]$
and
$I_{1}=[\varepsilon ,2-\varepsilon ]$
and
![]() $I_{-1}=[\varepsilon ,1-\varepsilon ]\cup [1+\varepsilon ,2-\varepsilon ]$
, let
$I_{-1}=[\varepsilon ,1-\varepsilon ]\cup [1+\varepsilon ,2-\varepsilon ]$
, let
![]() $a\in C_0(X)$
be constant equal to 1 on
$a\in C_0(X)$
be constant equal to 1 on
![]() $I_1$
and linear otherwise, and let
$I_1$
and linear otherwise, and let
![]() $b=\sigma (b)\in C_0(U)=C_0(X)_{-1}$
be constant equal to 1 on
$b=\sigma (b)\in C_0(U)=C_0(X)_{-1}$
be constant equal to 1 on
![]() $I_{-1}$
and linear otherwise. Let
$I_{-1}$
and linear otherwise. Let
![]() $f_{-1}=(\xi _{-1},\eta _{-1})\in C_0(U)\oplus C_0(U)$
and
$f_{-1}=(\xi _{-1},\eta _{-1})\in C_0(U)\oplus C_0(U)$
and
![]() $f_1=(\xi _1,\eta _1)\in C_0(X)\oplus C_0(X)$
be a Rokhlin tower for
$f_1=(\xi _1,\eta _1)\in C_0(X)\oplus C_0(X)$
be a Rokhlin tower for
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $F=\{(a,a),(b,b)\}$
and
$F=\{(a,a),(b,b)\}$
and
![]() $\varepsilon $
. Then we have:
$\varepsilon $
. Then we have:
-
(a)
 $|\xi _{-1}(\sigma (x))b(x)-\eta _1(x)b(x)|<\varepsilon $
and
$|\xi _{-1}(\sigma (x))b(x)-\eta _1(x)b(x)|<\varepsilon $
and
 $|\eta _{-1}(\sigma (x))b(x)-\xi _1(x)b(x)|<\varepsilon $
;
$|\eta _{-1}(\sigma (x))b(x)-\xi _1(x)b(x)|<\varepsilon $
; -
(b)
 $\xi _{-1}(x)\xi _1(x)a(x)<\varepsilon $
and
$\xi _{-1}(x)\xi _1(x)a(x)<\varepsilon $
and
 $\eta _{-1}(x)\eta _1(x)a(x)<\varepsilon $
;
$\eta _{-1}(x)\eta _1(x)a(x)<\varepsilon $
; -
(c)
 $(1-\xi _{-1}(x)-\xi _1(x))a(x)<\varepsilon $
and
$(1-\xi _{-1}(x)-\xi _1(x))a(x)<\varepsilon $
and
 $(1-\eta _{-1}(x)-\eta _1(x))a(x)<\varepsilon $
$(1-\eta _{-1}(x)-\eta _1(x))a(x)<\varepsilon $
for all
![]() $x\in X$
. Upon making a small renormalization, we may assume that
$x\in X$
. Upon making a small renormalization, we may assume that
for all
![]() $x\in I_1$
. In particular,
$x\in I_1$
. In particular,
![]() $\xi _1(1)=1$
. Fix
$\xi _1(1)=1$
. Fix
![]() $x\in I_1$
. Substituting (3.1) into (b), we get
$x\in I_1$
. Substituting (3.1) into (b), we get
which yields either
![]() $\xi _1(x)> 3/4$
or
$\xi _1(x)> 3/4$
or
![]() $\xi _1(x)<1/4$
. Since
$\xi _1(x)<1/4$
. Since
![]() $\xi _1$
is continuous, we must have either
$\xi _1$
is continuous, we must have either
![]() $\xi _1(I_{1})\subseteq (3/4,1]$
or
$\xi _1(I_{1})\subseteq (3/4,1]$
or
![]() $\xi _1(I_{1})\subseteq [0,1/4)$
, and since
$\xi _1(I_{1})\subseteq [0,1/4)$
, and since
![]() $\xi _1(1)=1$
, it must be
$\xi _1(1)=1$
, it must be
![]() $\xi _1(I_{1})\subseteq (3/4,1]$
and thus
$\xi _1(I_{1})\subseteq (3/4,1]$
and thus
An identical argument shows that
Taking now
![]() $x\in I_{-1}\subseteq I_1$
, and noting that
$x\in I_{-1}\subseteq I_1$
, and noting that
![]() $b(x)=1$
and
$b(x)=1$
and
![]() $\sigma (x)\in I_{-1}$
as well, we get
$\sigma (x)\in I_{-1}$
as well, we get
which is a contradiction. We conclude that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )>0$
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )>0$
.
We point out that one can construct towers that witness the fact that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq 1$
, thus allowing us to conclude that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq 1$
, thus allowing us to conclude that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )=1$
. However, we do not need this, so we omit it.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )=1$
. However, we do not need this, so we omit it.
In contrast with the previous example, we will show in Theorem 3.4 that for globalizable partial actions which act on unital
![]() $C^*$
-algebras, their Rokhlin dimension (with or without commuting towers) agrees with that of their globalization. The result is by no means obvious and its proof is quite technical. The following lemma, which deals exclusively with global actions, represents the first step in proving the inequality
$C^*$
-algebras, their Rokhlin dimension (with or without commuting towers) agrees with that of their globalization. The result is by no means obvious and its proof is quite technical. The following lemma, which deals exclusively with global actions, represents the first step in proving the inequality
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
.
Lemma 3.3. Let
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
be an action of a finite group G on a unital
$\beta \colon G\to {\mathrm {Aut}}(B)$
be an action of a finite group G on a unital
![]() $C^*$
-algebra B. Let A be a unital ideal in B satisfying
$C^*$
-algebra B. Let A be a unital ideal in B satisfying
![]() $B=\overline {\mathrm {span}}\{\beta _g(a)\colon a\in A, g\in G \}$
. If
$B=\overline {\mathrm {span}}\{\beta _g(a)\colon a\in A, g\in G \}$
. If
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
is finite, then there exist Rokhlin towers
$d={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
is finite, then there exist Rokhlin towers
![]() $f_g^{(j)}\in B$
for
$f_g^{(j)}\in B$
for
![]() $\beta $
, satisfying condition (1’) in Proposition
2.4
, such that
$\beta $
, satisfying condition (1’) in Proposition
2.4
, such that
![]() $f_1^{(0)},\ldots ,f_1^{(d)}$
belong to A. A similar statement holds when
$f_1^{(0)},\ldots ,f_1^{(d)}$
belong to A. A similar statement holds when
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )<\infty $
.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )<\infty $
.
Proof We divide the proof into claims.
Claim 1. There exist projections
![]() $p_g\in A$
, for
$p_g\in A$
, for
![]() $g\in G$
, which are central in B and satisfy
$g\in G$
, which are central in B and satisfy
![]() $1_B=\sum \nolimits _{g\in G}\beta _g(p_g)$
.
$1_B=\sum \nolimits _{g\in G}\beta _g(p_g)$
.
Set
![]() $n=|G|$
and fix an enumeration
$n=|G|$
and fix an enumeration
![]() $G=\{1_G=g_1,g_2,\ldots ,g_n\}$
. Since
$G=\{1_G=g_1,g_2,\ldots ,g_n\}$
. Since
![]() $B\!=\!\!\sum _{g\in G}\!\beta _g\!(A)$
, we have
$B\!=\!\!\sum _{g\in G}\!\beta _g\!(A)$
, we have
![]() $1_B\leq \sum \nolimits _{g\in G}\beta _g(1_A)$
. Note that the projections
$1_B\leq \sum \nolimits _{g\in G}\beta _g(1_A)$
. Note that the projections
![]() $\beta _g(1_A)$
are central and therefore together with
$\beta _g(1_A)$
are central and therefore together with
![]() $1_B$
generate a commutative
$1_B$
generate a commutative
![]() $C^*$
-algebra. In the rest of this claim, we regard
$C^*$
-algebra. In the rest of this claim, we regard
![]() $1_B$
and
$1_B$
and
![]() $\beta _g(1_A)$
, for
$\beta _g(1_A)$
, for
![]() $g\in G$
, as
$g\in G$
, as
![]() $\{0,1\}$
-valued functions on some compact Hausdorff space and identify them with their supports. In particular, the support of
$\{0,1\}$
-valued functions on some compact Hausdorff space and identify them with their supports. In particular, the support of
![]() $1_B$
is equal to the union of the supports of
$1_B$
is equal to the union of the supports of
![]() $\beta _g(1_A)$
, for
$\beta _g(1_A)$
, for
![]() $g\in G$
. By successively removing the double intersections, adding the triple intersections, and proceeding similarly for higher degrees, we can write
$g\in G$
. By successively removing the double intersections, adding the triple intersections, and proceeding similarly for higher degrees, we can write
![]() $1_B$
as follows:
$1_B$
as follows:
 $$ \begin{align} 1_B=&\sum\limits_{i=1}^{n}\beta_{g_i}(1_A)-\sum\limits_{1\leq i<j\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A) \notag\\ & + \sum_{1\leq i<j<k\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A)\beta_{g_k}(1_A) +\cdots \notag\\ & +(-1)^{n-1}\beta_{g_1}(1_A)\beta_{g_2}(1_A)\cdots\beta_{g_n}(1_A). \end{align} $$
$$ \begin{align} 1_B=&\sum\limits_{i=1}^{n}\beta_{g_i}(1_A)-\sum\limits_{1\leq i<j\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A) \notag\\ & + \sum_{1\leq i<j<k\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A)\beta_{g_k}(1_A) +\cdots \notag\\ & +(-1)^{n-1}\beta_{g_1}(1_A)\beta_{g_2}(1_A)\cdots\beta_{g_n}(1_A). \end{align} $$
Observe that every element appearing in (3.4) is central in B. We now proceed to write the unit of B as a sum of orthogonal projections in the following manner. The first summand consists of all the elements appearing in (3.4) that have
![]() $\beta _{g_1}(1_A)$
as a factor. The second summand consists of all the elements appearing in (3.4) that have
$\beta _{g_1}(1_A)$
as a factor. The second summand consists of all the elements appearing in (3.4) that have
![]() $\beta _{g_2}(1_A)$
as a factor but not
$\beta _{g_2}(1_A)$
as a factor but not
![]() $\beta _{g_1}(1_A)$
. Continue inductively, and note that the process finishes after n steps; indeed, the only element left at the nth step is
$\beta _{g_1}(1_A)$
. Continue inductively, and note that the process finishes after n steps; indeed, the only element left at the nth step is
![]() $\beta _{g_n}(1_A)$
.
$\beta _{g_n}(1_A)$
.
For
![]() $1\leq k\leq n$
, the kth summand is
$1\leq k\leq n$
, the kth summand is
 $$ \begin{align*} P_k &= \beta_{g_k}(1_A)-\sum\limits_{k<j\leq n}\beta_{g_k}(1_A)\beta_{g_j}(1_A)+\sum\limits_{k<i<j\leq n}\beta_{g_k}(1_A)\beta_{g_i}(1_A)\beta_{g_j}(1_A)\\ &\quad+\cdots +(-1)^{n-k}\beta_{g_k}(1_A)\beta_{g_{k+1}}(1_A)\cdots \beta_{g_n}(1_A), \end{align*} $$
$$ \begin{align*} P_k &= \beta_{g_k}(1_A)-\sum\limits_{k<j\leq n}\beta_{g_k}(1_A)\beta_{g_j}(1_A)+\sum\limits_{k<i<j\leq n}\beta_{g_k}(1_A)\beta_{g_i}(1_A)\beta_{g_j}(1_A)\\ &\quad+\cdots +(-1)^{n-k}\beta_{g_k}(1_A)\beta_{g_{k+1}}(1_A)\cdots \beta_{g_n}(1_A), \end{align*} $$
and we have
![]() $1_B=P_1+\cdots +P_n$
. We want to see that
$1_B=P_1+\cdots +P_n$
. We want to see that
![]() $P_k$
is a projection. Set
$P_k$
is a projection. Set
 $$ \begin{align*} Q_{k}=\sum\limits_{k<j\leq n}\beta_{g_j}(1_A)-\sum\limits_{k<i<j\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A)+\cdots + (-1)^{n-k+1}\prod_{j>k} \beta_{g_j}(1_A). \end{align*} $$
$$ \begin{align*} Q_{k}=\sum\limits_{k<j\leq n}\beta_{g_j}(1_A)-\sum\limits_{k<i<j\leq n}\beta_{g_i}(1_A)\beta_{g_j}(1_A)+\cdots + (-1)^{n-k+1}\prod_{j>k} \beta_{g_j}(1_A). \end{align*} $$
Then
![]() $Q_{k}$
is the unit of the ideal
$Q_{k}$
is the unit of the ideal
![]() $\sum \nolimits _{j>k}\beta _{g_j}(A)$
and therefore
$\sum \nolimits _{j>k}\beta _{g_j}(A)$
and therefore
![]() $Q_{k}$
is a projection. Moreover, an easy computation shows that
$Q_{k}$
is a projection. Moreover, an easy computation shows that
![]() $P_k=\beta _{g_k}(1_A)(1_B-Q_{k})$
and thus
$P_k=\beta _{g_k}(1_A)(1_B-Q_{k})$
and thus
![]() $P_k$
is also a projection. Note that
$P_k$
is also a projection. Note that
![]() $P_kP_\ell =0$
if
$P_kP_\ell =0$
if
![]() $k\neq \ell $
.
$k\neq \ell $
.
For
![]() $k=1,\ldots ,n$
, set
$k=1,\ldots ,n$
, set
![]() $p_k=\beta _{g_k}^{-1}(P_k)$
, which can be written as
$p_k=\beta _{g_k}^{-1}(P_k)$
, which can be written as
 $$ \begin{align*}p_k=1_A-\sum\limits_{k<j\leq n}1_A\beta_{{g_k}^{-1}g_j}(1_A)+\cdots +(-1)^{(n-k)}1_A\beta_{{g_k}^{-1}g_{k+1}}(1_A)\cdots \beta_{{g_k}^{-1}{g_n}}(1_A).\end{align*} $$
$$ \begin{align*}p_k=1_A-\sum\limits_{k<j\leq n}1_A\beta_{{g_k}^{-1}g_j}(1_A)+\cdots +(-1)^{(n-k)}1_A\beta_{{g_k}^{-1}g_{k+1}}(1_A)\cdots \beta_{{g_k}^{-1}{g_n}}(1_A).\end{align*} $$
Then
![]() $p_k$
is a central projection, and it belongs to A because
$p_k$
is a central projection, and it belongs to A because
![]() $1_A$
is a factor in each of its summands. Since
$1_A$
is a factor in each of its summands. Since
![]() $1_B=\sum _{k=1}^n \beta _{g_k}(p_k)$
, this concludes the proof of Claim 1.
$1_B=\sum _{k=1}^n \beta _{g_k}(p_k)$
, this concludes the proof of Claim 1.
Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $F\subseteq B$
be finite. Without loss of generality, F is
$F\subseteq B$
be finite. Without loss of generality, F is
![]() $\beta $
-invariant, contains
$\beta $
-invariant, contains
![]() $1_B$
, and consists of contractions. Set
$1_B$
, and consists of contractions. Set
![]() $\varepsilon _0={\varepsilon }/{|G|^2(d+2)}$
, and let
$\varepsilon _0={\varepsilon }/{|G|^2(d+2)}$
, and let
![]() $f_g^{(j)}\in B$
, for
$f_g^{(j)}\in B$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, be Rokhlin towers for
$j=0,\ldots ,d$
, be Rokhlin towers for
![]() $(F,\varepsilon _0)$
. Using Proposition 2.4 for the equality, and by replacing
$(F,\varepsilon _0)$
. Using Proposition 2.4 for the equality, and by replacing
![]() $f_g^{(j)}$
with
$f_g^{(j)}$
with
![]() $({1}/({1+\varepsilon })) f_g^{(j)}$
for the inequality, we may assume
$({1}/({1+\varepsilon })) f_g^{(j)}$
for the inequality, we may assume
 $$ \begin{align} \beta_g(f_h^{(j)})=f_{gh}^{(j)} \quad \mbox{and} \quad \sum\limits_{g\in G}\sum_{j=0}^df_g^{(j)}\leq 1 \end{align} $$
$$ \begin{align} \beta_g(f_h^{(j)})=f_{gh}^{(j)} \quad \mbox{and} \quad \sum\limits_{g\in G}\sum_{j=0}^df_g^{(j)}\leq 1 \end{align} $$
for all
![]() $g,h\in G$
and all
$g,h\in G$
and all
![]() $j=0,\ldots ,d$
.
$j=0,\ldots ,d$
.
Claim 2. There are positive elements
![]() $x_g^{(j)}\in A$
, for
$x_g^{(j)}\in A$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, for which:
$j=0,\ldots ,d$
, for which:
-
(2.a)
 $f_1^{(j)}=\sum \nolimits _{g\in G}\beta _g(x_g^{(j)})$
;
$f_1^{(j)}=\sum \nolimits _{g\in G}\beta _g(x_g^{(j)})$
; -
(2.b)
 $\sum \nolimits _{g\in G} x_g^{(j)}\in A$
is a positive contraction;
$\sum \nolimits _{g\in G} x_g^{(j)}\in A$
is a positive contraction; -
(2.c)
 $\beta _h(x_g^{(j)})b\approx _{\varepsilon _0}b\beta _h(x_g^{(j)})$
for all
$\beta _h(x_g^{(j)})b\approx _{\varepsilon _0}b\beta _h(x_g^{(j)})$
for all
 $b\in F$
, all
$b\in F$
, all
 $g,h\in G$
and all
$g,h\in G$
and all
 $j=0,\ldots ,d$
; and
$j=0,\ldots ,d$
; and -
(2.d)
 $\|x_h^{(j)}\beta _g(x_t^{(j)})\|<\varepsilon _0$
for all
$\|x_h^{(j)}\beta _g(x_t^{(j)})\|<\varepsilon _0$
for all
 $j=0,\ldots ,d$
and all
$j=0,\ldots ,d$
and all
 $g,h,t\in G$
with
$g,h,t\in G$
with
 $g\neq 1$
.
$g\neq 1$
.
Using Claim 1, fix projections
![]() $p_g\in A$
, for
$p_g\in A$
, for
![]() $g\in G$
, which are central in B and satisfy
$g\in G$
, which are central in B and satisfy
![]() $1_B=\sum _{g\in G}\beta _g(p_g)$
. For
$1_B=\sum _{g\in G}\beta _g(p_g)$
. For
![]() $j=0,\ldots ,d$
, multiply both sides of the identity by
$j=0,\ldots ,d$
, multiply both sides of the identity by
![]() $f_1^{(j)}$
to get
$f_1^{(j)}$
to get
 $$ \begin{align*} f_1^{(j)}=\sum\limits_{g\in G}\beta_{g}(\beta_{{g}^{-1}}(f_1^{(j)})p_g)=\sum\limits_{g\in G}\beta_{g}(f_{{g}^{-1}}^{(j)}p_g). \end{align*} $$
$$ \begin{align*} f_1^{(j)}=\sum\limits_{g\in G}\beta_{g}(\beta_{{g}^{-1}}(f_1^{(j)})p_g)=\sum\limits_{g\in G}\beta_{g}(f_{{g}^{-1}}^{(j)}p_g). \end{align*} $$
Set
![]() $x_{g}^{(j)}=f_{{g}^{-1}}^{(j)}p_g$
for all
$x_{g}^{(j)}=f_{{g}^{-1}}^{(j)}p_g$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
. Since
$j=0,\ldots ,d$
. Since
![]() $p_g$
is central in B and belongs to A, it is clear that
$p_g$
is central in B and belongs to A, it is clear that
![]() $x_g^{(j)}$
is a positive element in A. Condition (2.a) is satisfied by construction. Using centrality of
$x_g^{(j)}$
is a positive element in A. Condition (2.a) is satisfied by construction. Using centrality of
![]() $p_g$
at the second step, we get
$p_g$
at the second step, we get
 $$ \begin{align*}\sum\limits_{g\in G}x_{g}^{(j)}=\sum\limits_{g\in G}f_{{g}^{-1}}^{(j)}p_g\leq\sum\limits_{g\in G}f_{g}^{(j)}\leq\sum\limits_{j=0}^{d}\sum\limits_{g\in G}f_{g}^{(j)} \stackrel{(3.5)}{\leq} 1,\end{align*} $$
$$ \begin{align*}\sum\limits_{g\in G}x_{g}^{(j)}=\sum\limits_{g\in G}f_{{g}^{-1}}^{(j)}p_g\leq\sum\limits_{g\in G}f_{g}^{(j)}\leq\sum\limits_{j=0}^{d}\sum\limits_{g\in G}f_{g}^{(j)} \stackrel{(3.5)}{\leq} 1,\end{align*} $$
and thus
![]() $\sum \nolimits _{g\in G}x_{g}^{(j)}$
is a positive contraction, verifying (2.b). In order to check (2.c), let
$\sum \nolimits _{g\in G}x_{g}^{(j)}$
is a positive contraction, verifying (2.b). In order to check (2.c), let
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j=0,\ldots ,d$
. Since
$j=0,\ldots ,d$
. Since
![]() $\beta _h(x_g^{(j)})=f_{hg^{-1}}^{(j)}\beta _h(p_g)$
and
$\beta _h(x_g^{(j)})=f_{hg^{-1}}^{(j)}\beta _h(p_g)$
and
![]() $p_g$
is central, it follows that
$p_g$
is central, it follows that
for all
![]() $b\in F$
. We turn to (2.d). Given
$b\in F$
. We turn to (2.d). Given
![]() $j=0,\ldots ,d$
and
$j=0,\ldots ,d$
and
![]() $g,h,t\in G$
with
$g,h,t\in G$
with
![]() $g\neq 1$
, we have
$g\neq 1$
, we have
If
![]() $gt^{-1}\neq h^{-1}$
then
$gt^{-1}\neq h^{-1}$
then
![]() $\|f_{{h}^{-1}}^{(j)}f_{gt^{-1}}^{(j)}\|<\varepsilon _0$
and hence
$\|f_{{h}^{-1}}^{(j)}f_{gt^{-1}}^{(j)}\|<\varepsilon _0$
and hence
![]() $\|x_h^{(j)}\beta _g(x_t^{(j)})\|<\varepsilon _0$
. Otherwise, we have
$\|x_h^{(j)}\beta _g(x_t^{(j)})\|<\varepsilon _0$
. Otherwise, we have
![]() $gt^{-1}= h^{-1}$
and thus
$gt^{-1}= h^{-1}$
and thus
![]() $g=h^{-1}t$
. In particular,
$g=h^{-1}t$
. In particular,
![]() $h\neq t$
. Then
$h\neq t$
. Then
since
![]() $\beta _t(p_t)$
is orthogonal to
$\beta _t(p_t)$
is orthogonal to
![]() $\beta _h(p_h)$
by Claim 1. It follows that
$\beta _h(p_h)$
by Claim 1. It follows that
![]() $x_h^{(j)}\beta _g(x_t^{(j)})=0$
, and thus (2.d) is satisfied. This proves Claim 2.
$x_h^{(j)}\beta _g(x_t^{(j)})=0$
, and thus (2.d) is satisfied. This proves Claim 2.
Let
![]() $x_g^{(j)}\in A$
, for
$x_g^{(j)}\in A$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, be positive elements satisfying the conclusion of Claim 2. For
$j=0,\ldots ,d$
, be positive elements satisfying the conclusion of Claim 2. For
![]() $j=0,\ldots ,d$
, set
$j=0,\ldots ,d$
, set
![]() $a_1^{(j)}=\sum \nolimits _{g\in G}x_g^{(j)}\in A$
. For
$a_1^{(j)}=\sum \nolimits _{g\in G}x_g^{(j)}\in A$
. For
![]() $g\in G$
, we set
$g\in G$
, we set
![]() $a_g^{(j)}=\beta _g(a_1^{(j)})$
. Then
$a_g^{(j)}=\beta _g(a_1^{(j)})$
. Then
![]() $\beta _g(a_h^{(j)})=a_{gh}^{(j)}$
for all
$\beta _g(a_h^{(j)})=a_{gh}^{(j)}$
for all
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j=0,\ldots ,d$
. In particular, condition (1) in Definition 2.1 is satisfied. To check condition (2), let
$j=0,\ldots ,d$
. In particular, condition (1) in Definition 2.1 is satisfied. To check condition (2), let
![]() $j=0,\ldots ,d$
and
$j=0,\ldots ,d$
and
![]() $g,h\in G$
with
$g,h\in G$
with
![]() $g\neq h$
. Then
$g\neq h$
. Then
 $$ \begin{align*}\|a_g^{(j)}a_h^{(j)}\|=\|a_1^{(j)}\beta_{g^{-1}h}(a_1^{(j)})\|=\bigg\|\sum\limits_{s,t\in G}x_s^{(j)}\beta_{g^{-1}h}(x_t^{(j)})\bigg\|\stackrel{\mathrm{(2.d)}}{\leq} |G|^2\varepsilon_0<\varepsilon.\end{align*} $$
$$ \begin{align*}\|a_g^{(j)}a_h^{(j)}\|=\|a_1^{(j)}\beta_{g^{-1}h}(a_1^{(j)})\|=\bigg\|\sum\limits_{s,t\in G}x_s^{(j)}\beta_{g^{-1}h}(x_t^{(j)})\bigg\|\stackrel{\mathrm{(2.d)}}{\leq} |G|^2\varepsilon_0<\varepsilon.\end{align*} $$
Moreover, condition (3) follows from the following identity:
 $$ \begin{align*} \sum\limits_{g\in G}\sum\limits_{j=0}^{d}a_g^{(j)}&=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g\bigg(\sum\limits_{h\in G} x_h^{(j)}\bigg)=\sum\limits_{g,h\in G}\sum\limits_{j=0}^{d}\beta_{g}(x_h^{(j)}) \\ &=\sum\limits_{g,h\in G}\sum\limits_{j=0}^{d}\beta_{gh}(x_h^{(j)}) =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g\bigg(\sum\limits_{h\in G} \beta_h(x_h^{(j)})\bigg)\\ &= \sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(f_1^{(j)}) =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}f_g^{(j)}. \end{align*} $$
$$ \begin{align*} \sum\limits_{g\in G}\sum\limits_{j=0}^{d}a_g^{(j)}&=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g\bigg(\sum\limits_{h\in G} x_h^{(j)}\bigg)=\sum\limits_{g,h\in G}\sum\limits_{j=0}^{d}\beta_{g}(x_h^{(j)}) \\ &=\sum\limits_{g,h\in G}\sum\limits_{j=0}^{d}\beta_{gh}(x_h^{(j)}) =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g\bigg(\sum\limits_{h\in G} \beta_h(x_h^{(j)})\bigg)\\ &= \sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(f_1^{(j)}) =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}f_g^{(j)}. \end{align*} $$
Let
![]() $b\in F$
,
$b\in F$
,
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
. In order to check condition (4) in Definition 2.1, and since
$j=0,\ldots ,d$
. In order to check condition (4) in Definition 2.1, and since
![]() $a_g^{(j)}=\beta _g(a_1^{(j)})$
and F is
$a_g^{(j)}=\beta _g(a_1^{(j)})$
and F is
![]() $\beta $
-invariant, it suffices to take
$\beta $
-invariant, it suffices to take
![]() $g=1$
. In this case, we have
$g=1$
. In this case, we have
 $$ \begin{align*}\|a_1^{(j)}b-ba_1^{(j)}\|\leq \sum_{g\in G}\|x_g^{(j)}b-bx_g^{(j)}\|\stackrel{\mathrm{(2.c)}}{\leq} |G|\varepsilon_0<\varepsilon.\end{align*} $$
$$ \begin{align*}\|a_1^{(j)}b-ba_1^{(j)}\|\leq \sum_{g\in G}\|x_g^{(j)}b-bx_g^{(j)}\|\stackrel{\mathrm{(2.c)}}{\leq} |G|\varepsilon_0<\varepsilon.\end{align*} $$
This proves the first part of the lemma.
Assume now that
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )=d<\infty $
, and choose the Rokhlin towers as above to moreover satisfy condition (5) in Definition 2.1. For
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )=d<\infty $
, and choose the Rokhlin towers as above to moreover satisfy condition (5) in Definition 2.1. For
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j,k=0,\ldots ,d$
, we get
$j,k=0,\ldots ,d$
, we get
 $$ \begin{align*}a_g^{(j)}a_h^{(k)} &= \beta_g(a_1^{(j)})\beta_h(a_1^{(k)})=\sum_{t,s\in G} \beta_g(x_t^{(j)})\beta_h(x_s^{(k)})\\ &=\sum_{t,s\in G} \beta_g(f_{t^{-1}}^{(j)}p_t)\beta_h(f_{s^{-1}}^{(k)}p_s) =\sum_{t,s\in G} f_{gt^{-1}}^{(j)}\beta_g(p_t)f_{hs^{-1}}^{(k)}\beta_h(p_s)\\ &\approx_{|G|^2\varepsilon_0}\sum_{t,s\in G} f_{hs^{-1}}^{(k)}\beta_h(p_s)f_{gt^{-1}}^{(j)}\beta_g(p_t) =a_h^{(k)}a_g^{(j)}.\\[-46pt] \end{align*} $$
$$ \begin{align*}a_g^{(j)}a_h^{(k)} &= \beta_g(a_1^{(j)})\beta_h(a_1^{(k)})=\sum_{t,s\in G} \beta_g(x_t^{(j)})\beta_h(x_s^{(k)})\\ &=\sum_{t,s\in G} \beta_g(f_{t^{-1}}^{(j)}p_t)\beta_h(f_{s^{-1}}^{(k)}p_s) =\sum_{t,s\in G} f_{gt^{-1}}^{(j)}\beta_g(p_t)f_{hs^{-1}}^{(k)}\beta_h(p_s)\\ &\approx_{|G|^2\varepsilon_0}\sum_{t,s\in G} f_{hs^{-1}}^{(k)}\beta_h(p_s)f_{gt^{-1}}^{(j)}\beta_g(p_t) =a_h^{(k)}a_g^{(j)}.\\[-46pt] \end{align*} $$
We are now ready to prove the main result of this section: the Rokhlin dimension of a globalizable partial action on a unital
![]() $C^*$
-algebra equals the Rokhlin dimension of its globalization. In particular, we obtain a large family of examples of partial actions with finite Rokhlin dimension.
$C^*$
-algebra equals the Rokhlin dimension of its globalization. In particular, we obtain a large family of examples of partial actions with finite Rokhlin dimension.
Theorem 3.4. Let
![]() $\alpha $
be a globalizable partial action of a finite group G on a unital
$\alpha $
be a globalizable partial action of a finite group G on a unital
![]() $C^*$
-algebra A, and let
$C^*$
-algebra A, and let
![]() $\beta \colon G\to {\mathrm {Aut}}(B)$
denote its globalization. Then
$\beta \colon G\to {\mathrm {Aut}}(B)$
denote its globalization. Then
Proof The proofs for
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
and
${\mathrm {dim}_{\mathrm {Rok}}}$
and
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
are very similar, so we provide full details for
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
are very similar, so we provide full details for
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
and indicate how one modifies the proof to obtain the result for
${\mathrm {dim}_{\mathrm {Rok}}}$
and indicate how one modifies the proof to obtain the result for
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. We divide the proof into two parts, namely the inequalities
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. We divide the proof into two parts, namely the inequalities
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
and
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
and
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\geq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
. Since A is unital and
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\geq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
. Since A is unital and
![]() $\alpha $
is globalizable, it follows that
$\alpha $
is globalizable, it follows that
![]() $A_g$
is unital for all
$A_g$
is unital for all
![]() $g\in G$
, with unit given by
$g\in G$
, with unit given by
![]() $1_g=1_A\beta _g(1_A)$
.
$1_g=1_A\beta _g(1_A)$
.
To show that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
, it suffices to assume that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
, it suffices to assume that
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
is finite. Let
$d={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
is finite. Let
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $F\subseteq A$
be given. Using Lemma 3.3, let
$F\subseteq A$
be given. Using Lemma 3.3, let
![]() $\widetilde {f}_g^{(j)}\in B$
, for
$\widetilde {f}_g^{(j)}\in B$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, such that:
$j=0,\ldots ,d$
, such that:
-
(a)
 $\beta _g(\widetilde {f}_h^{(j)})=\widetilde {f}_{gh}^{(j)}$
for all
$\beta _g(\widetilde {f}_h^{(j)})=\widetilde {f}_{gh}^{(j)}$
for all
 $g,h\in G$
and
$g,h\in G$
and
 $j=0,\ldots ,d$
;
$j=0,\ldots ,d$
; -
(b)
 $\|\widetilde {f}_g^{(j)}\widetilde {f}_h^{(j)}\|<\varepsilon $
for all
$\|\widetilde {f}_g^{(j)}\widetilde {f}_h^{(j)}\|<\varepsilon $
for all
 $j=0,\ldots ,d$
and all
$j=0,\ldots ,d$
and all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
;
$g\neq h$
; -
(c)
 $\| 1_B-\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^d \widetilde {f}_g^{(j)}\|\leq \varepsilon $
;
$\| 1_B-\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^d \widetilde {f}_g^{(j)}\|\leq \varepsilon $
; -
(d)
 $\|\widetilde {f}_g^{(j)}b-b\widetilde {f}_g^{(j)}\|<\varepsilon $
for all
$\|\widetilde {f}_g^{(j)}b-b\widetilde {f}_g^{(j)}\|<\varepsilon $
for all
 $g\in G$
, all
$g\in G$
, all
 $j=0,\ldots ,d$
and all
$j=0,\ldots ,d$
and all
 $b\in F$
.
$b\in F$
.
Set
![]() $f_g^{(j)}=\widetilde {f}_g^{(j)}1_g\in A_g$
for all
$f_g^{(j)}=\widetilde {f}_g^{(j)}1_g\in A_g$
for all
![]() $g\in G$
and all
$g\in G$
and all
![]() $j=0,\ldots ,d$
. We claim that these are Rokhlin towers for
$j=0,\ldots ,d$
. We claim that these are Rokhlin towers for
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $(F,\varepsilon )$
. For
$(F,\varepsilon )$
. For
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j=0,\ldots ,d$
, we use at the second step that
$j=0,\ldots ,d$
, we use at the second step that
![]() $\beta _g|_{A_{g^{-1}}}=\alpha _g$
to get
$\beta _g|_{A_{g^{-1}}}=\alpha _g$
to get
thus verifying condition (1) in Definition 2.1. Moreover,
![]() $\|f_g^{(j)}f_h^{(j)}\| \leq \|\widetilde {f}_g^{(j)}\widetilde {f}_h^{(j)}\|$
and hence condition (2) is also satisfied by (b) above. Since
$\|f_g^{(j)}f_h^{(j)}\| \leq \|\widetilde {f}_g^{(j)}\widetilde {f}_h^{(j)}\|$
and hence condition (2) is also satisfied by (b) above. Since
 $$ \begin{align*} \sum\limits_{g\in G}\sum\limits_{j=0}^{d}f_g^{(j)}&=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(\widetilde{f}_1^{(j)})1_g =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(\widetilde{f}_1^{(j)}1_A)\beta_g(1_A)1_A=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\widetilde{f}_g^{(j)}1_A, \end{align*} $$
$$ \begin{align*} \sum\limits_{g\in G}\sum\limits_{j=0}^{d}f_g^{(j)}&=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(\widetilde{f}_1^{(j)})1_g =\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\beta_g(\widetilde{f}_1^{(j)}1_A)\beta_g(1_A)1_A=\sum\limits_{g\in G}\sum\limits_{j=0}^{d}\widetilde{f}_g^{(j)}1_A, \end{align*} $$
it follows from (c) that condition (3) is also satisfied. Finally, given
![]() $b\in F$
,
$b\in F$
,
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, we have
$j=0,\ldots ,d$
, we have
establishing condition (4). It follows that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, as desired. Note that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, as desired. Note that
for all
![]() $g,h\in G$
and
$g,h\in G$
and
![]() $j,k=0,\ldots ,d$
. Thus, if
$j,k=0,\ldots ,d$
. Thus, if
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )\leq d$
and the Rokhlin towers
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )\leq d$
and the Rokhlin towers
![]() $\widetilde {f}_g^{(j)}$
for
$\widetilde {f}_g^{(j)}$
for
![]() $\beta $
also satisfy condition (5) in Definition 2.1, then the Rokhlin towers
$\beta $
also satisfy condition (5) in Definition 2.1, then the Rokhlin towers
![]() $f_g^{(j)}$
for
$f_g^{(j)}$
for
![]() $\alpha $
also satisfy (5) and hence
$\alpha $
also satisfy (5) and hence
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
.
We turn to the inequality
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
, so we set
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
, so we set
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
and assume that
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
and assume that
![]() $d<\infty $
. Let
$d<\infty $
. Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $F\subseteq B$
be a finite subset. Without loss of generality, we assume that F contains
$F\subseteq B$
be a finite subset. Without loss of generality, we assume that F contains
![]() $1_g$
for all
$1_g$
for all
![]() $g\in G$
and that it is
$g\in G$
and that it is
![]() $\beta $
-invariant. Since B is generated by the
$\beta $
-invariant. Since B is generated by the
![]() $\beta $
-translations of A (condition (d) in Definition 3.1), there exist
$\beta $
-translations of A (condition (d) in Definition 3.1), there exist
![]() $a_g\in A$
for
$a_g\in A$
for
![]() $g\in G$
such that
$g\in G$
such that
![]() $1_B=\sum \nolimits _{g\in G}\beta _g(a_g)$
. Set
$1_B=\sum \nolimits _{g\in G}\beta _g(a_g)$
. Set
![]() $\varepsilon _0= {\varepsilon }/{|G|\max \nolimits _{g\in G}\|a_g\|}$
. Using Proposition 2.4, let
$\varepsilon _0= {\varepsilon }/{|G|\max \nolimits _{g\in G}\|a_g\|}$
. Using Proposition 2.4, let
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, be positive contractions satisfying the following conditions:
$j=0,\ldots ,d$
, be positive contractions satisfying the following conditions:
-
(i)
 $\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_{g}$
for all
$\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_{g}$
for all
 $g,h\in G$
and
$g,h\in G$
and
 $j=0,\ldots ,d$
;
$j=0,\ldots ,d$
; -
(ii)
 $\|f_g^{(j)}f_h^{(j)}\|<\varepsilon $
for all
$\|f_g^{(j)}f_h^{(j)}\|<\varepsilon $
for all
 $j=0,\ldots ,d$
and all
$j=0,\ldots ,d$
and all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
;
$g\neq h$
; -
(iii)
 $\|\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^d f_g^{(j)}-1_A\|<\varepsilon $
.
$\|\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^d f_g^{(j)}-1_A\|<\varepsilon $
. -
(iv)
 $\|f_g^{(j)}b-bf_g^{(j)}\|<\varepsilon $
for all
$\|f_g^{(j)}b-bf_g^{(j)}\|<\varepsilon $
for all
 $g\in G$
, all
$g\in G$
, all
 $j=0,\ldots ,d$
and all
$j=0,\ldots ,d$
and all
 $b\in F$
.
$b\in F$
.
For
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, set
$j=0,\ldots ,d$
, set
![]() $\widetilde {f}_g^{(j)}=\beta _g(f_1^{(j)})\in B$
. We claim that the
$\widetilde {f}_g^{(j)}=\beta _g(f_1^{(j)})\in B$
. We claim that the
![]() $\widetilde {f}_g^{(j)}$
are Rokhlin towers for
$\widetilde {f}_g^{(j)}$
are Rokhlin towers for
![]() $\beta $
with respect to
$\beta $
with respect to
![]() $(F, \varepsilon )$
. Condition (1) in Definition 2.1 is clearly satisfied. In order to check (2), let
$(F, \varepsilon )$
. Condition (1) in Definition 2.1 is clearly satisfied. In order to check (2), let
![]() $j=0,\ldots ,d$
and
$j=0,\ldots ,d$
and
![]() $g,h\in G$
with
$g,h\in G$
with
![]() $g\neq h$
be given. Using that
$g\neq h$
be given. Using that
![]() $f_1^{(j)}=f_1^{(j)}1_A$
at the second step, and that
$f_1^{(j)}=f_1^{(j)}1_A$
at the second step, and that
![]() $1_{g^{-1}h}=1_A\beta _{g^{-1}h}(1_A)$
at the third, we get
$1_{g^{-1}h}=1_A\beta _{g^{-1}h}(1_A)$
at the third, we get
 $$ \begin{align*}\|\widetilde{f}_g^{(j)}\widetilde{f}_h^{(j)}\|&=\|\beta_g(f_1^{(j)})\beta_h(f_1^{(j)})\| =\|f_1^{(j)}1_A\beta_{g^{-1}h}(1_Af_1^{(j)})\|\\ &=\|f_1^{(j)}1_{g^{-1}h}\beta_{g^{-1}h}(f_1^{(j)})\| =\|f_1^{(j)}\alpha_{g^{-1}h}(1_{h^{-1}g}f_1^{(j)})\|\\ & \stackrel{\mathrm{(i)}}{=} \|f_1^{(j)}f_{g^{-1}h}^{(j)}\|\stackrel{\mathrm{(ii)}}{<} \varepsilon_0. \end{align*} $$
$$ \begin{align*}\|\widetilde{f}_g^{(j)}\widetilde{f}_h^{(j)}\|&=\|\beta_g(f_1^{(j)})\beta_h(f_1^{(j)})\| =\|f_1^{(j)}1_A\beta_{g^{-1}h}(1_Af_1^{(j)})\|\\ &=\|f_1^{(j)}1_{g^{-1}h}\beta_{g^{-1}h}(f_1^{(j)})\| =\|f_1^{(j)}\alpha_{g^{-1}h}(1_{h^{-1}g}f_1^{(j)})\|\\ & \stackrel{\mathrm{(i)}}{=} \|f_1^{(j)}f_{g^{-1}h}^{(j)}\|\stackrel{\mathrm{(ii)}}{<} \varepsilon_0. \end{align*} $$
To check (3), it suffices to show that for any
![]() $a\in A$
and
$a\in A$
and
![]() $h\in G$
, we have
$h\in G$
, we have
 $$ \begin{align*}\bigg\|\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}\beta_h(a)-\beta_h(a)\bigg\|<\|a\|\varepsilon_0.\end{align*} $$
$$ \begin{align*}\bigg\|\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}\beta_h(a)-\beta_h(a)\bigg\|<\|a\|\varepsilon_0.\end{align*} $$
Indeed, once this is established, and since
![]() $1_B=\sum \nolimits _{h\in G}\beta _h(a_h)$
, it will follow that
$1_B=\sum \nolimits _{h\in G}\beta _h(a_h)$
, it will follow that
 $$ \begin{align*}\bigg\|\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}-1_B\bigg\|< |G|\max_{g\in G}\|a_g\|\varepsilon_0=\varepsilon,\end{align*} $$
$$ \begin{align*}\bigg\|\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}-1_B\bigg\|< |G|\max_{g\in G}\|a_g\|\varepsilon_0=\varepsilon,\end{align*} $$
thus establishing (3). Let
![]() $a\in A$
and
$a\in A$
and
![]() $h\in G$
be given; without loss of generality we assume that
$h\in G$
be given; without loss of generality we assume that
![]() $\|a\|\leq 1$
. Then:
$\|a\|\leq 1$
. Then:
 $$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}\beta_h(a)&=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_g(f_1^{(j)})\beta_h(a)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\beta_{h^{-1}g}(f_1^{(j)}1_A)1_Aa)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\beta_{h^{-1}g}(f_1^{(j)}1_A\beta_{g^{-1}h}(1_A))a)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\alpha_{h^{-1}g}(f_1^{(j)}1_{g^{-1}h})a)\\ &\stackrel{\mathrm{(i)}}{=}\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(f_{h^{-1}g}^{(j)}a)\\ &\stackrel{\!\mathrm{(iii)}}{\, \approx_\varepsilon}_{\!_0}\! \beta_h(a), \end{align*} $$
$$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G}\widetilde{f}_g^{(j)}\beta_h(a)&=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_g(f_1^{(j)})\beta_h(a)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\beta_{h^{-1}g}(f_1^{(j)}1_A)1_Aa)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\beta_{h^{-1}g}(f_1^{(j)}1_A\beta_{g^{-1}h}(1_A))a)\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(\alpha_{h^{-1}g}(f_1^{(j)}1_{g^{-1}h})a)\\ &\stackrel{\mathrm{(i)}}{=}\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\beta_h(f_{h^{-1}g}^{(j)}a)\\ &\stackrel{\!\mathrm{(iii)}}{\, \approx_\varepsilon}_{\!_0}\! \beta_h(a), \end{align*} $$
as desired. Finally, to check condition (4), let
![]() $a\in F$
,
$a\in F$
,
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
be given. Using at the last step that
$j=0,\ldots ,d$
be given. Using at the last step that
![]() $\beta _{g^{-1}}(a)\in F$
, we get
$\beta _{g^{-1}}(a)\in F$
, we get
 $$ \begin{align*} \|\widetilde{f}_g^{(j)}a-a\widetilde{f}_g^{(j)}\|&=\|\beta_g(f_1^{(j)})a-a\beta_g(f_1^{(j)})\|\\ &=\|f_1^{(j)}\beta_{g^{-1}}(a)-\beta_{g^{-1}}(a)f_1^{(j)}\|\stackrel{\mathrm{(iv)}}{<}\varepsilon_0.\end{align*} $$
$$ \begin{align*} \|\widetilde{f}_g^{(j)}a-a\widetilde{f}_g^{(j)}\|&=\|\beta_g(f_1^{(j)})a-a\beta_g(f_1^{(j)})\|\\ &=\|f_1^{(j)}\beta_{g^{-1}}(a)-\beta_{g^{-1}}(a)f_1^{(j)}\|\stackrel{\mathrm{(iv)}}{<}\varepsilon_0.\end{align*} $$
This shows that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
. Observe that the Rokhlin towers for
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
. Observe that the Rokhlin towers for
![]() $\beta $
that we constructed satisfy the following identity for all
$\beta $
that we constructed satisfy the following identity for all
![]() $j,k=0,\ldots ,d$
and
$j,k=0,\ldots ,d$
and
![]() $g,h\in G$
:
$g,h\in G$
:
 $$ \begin{align*} \widetilde{f}_g^{(j)}\widetilde{f}_h^{(k)}&=\beta_g(f_1^{(j)})\beta_h(f_1^{(k)})=\beta_g(f_1^{(j)}1_A\beta_{g^{-1}h}(1_Af_1^{(k)}))\\ &=\beta_g(f_1^{(j)}\alpha_{g^{-1}h}(1_{h^{-1}g}f_1^{(k)})) = \beta_g(f_1^{(j)}f_{g^{-1}h}^{(k)}).\end{align*} $$
$$ \begin{align*} \widetilde{f}_g^{(j)}\widetilde{f}_h^{(k)}&=\beta_g(f_1^{(j)})\beta_h(f_1^{(k)})=\beta_g(f_1^{(j)}1_A\beta_{g^{-1}h}(1_Af_1^{(k)}))\\ &=\beta_g(f_1^{(j)}\alpha_{g^{-1}h}(1_{h^{-1}g}f_1^{(k)})) = \beta_g(f_1^{(j)}f_{g^{-1}h}^{(k)}).\end{align*} $$
By taking adjoints, we also get
![]() $\widetilde {f}_h^{(k)}\widetilde {f}_g^{(j)}= \beta _g(f_{g^{-1}h}^{(k)}f_1^{(j)})$
. In particular,
$\widetilde {f}_h^{(k)}\widetilde {f}_g^{(j)}= \beta _g(f_{g^{-1}h}^{(k)}f_1^{(j)})$
. In particular,
Thus, if
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
and the Rokhlin towers
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )\leq d$
and the Rokhlin towers
![]() $f_g^{(j)}$
for
$f_g^{(j)}$
for
![]() $\alpha $
also satisfy condition (5) in Definition 2.1, then the Rokhlin towers
$\alpha $
also satisfy condition (5) in Definition 2.1, then the Rokhlin towers
![]() $\widetilde {f}_g^{(j)}$
for
$\widetilde {f}_g^{(j)}$
for
![]() $\beta $
also satisfy (5) and hence
$\beta $
also satisfy (5) and hence
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )\!\leq ~d$
.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\beta )\!\leq ~d$
.
4 Structure of the crossed product
Since its introduction in [Reference Hirshberg, Winter and Zacharias18], the Rokhlin dimension has predominantly been used to study structural properties of the associated crossed products. Of greatest relevance are those properties related to the classification programme for nuclear
![]() $C^*$
-algebras, such as the UCT, finiteness of the nuclear dimension, absorption of a strongly self-absorbing
$C^*$
-algebras, such as the UCT, finiteness of the nuclear dimension, absorption of a strongly self-absorbing
![]() $C^*$
-algebra [Reference Toms and Winter24], or divisibility properties on K-theory.
$C^*$
-algebra [Reference Toms and Winter24], or divisibility properties on K-theory.
In this section, we explore the structure of the crossed products and fixed point algebras of partial actions with finite Rokhlin dimension. Our approach makes use of the decomposition property introduced and studied in [Reference Abadie, Gardella and Geffen2], which we recall in §4.1. For unital partial actions, a more direct argument can be given, which even yields better results (notably in the zero-dimensional case). In this setting, we show that the crossed product is Morita equivalent to the fixed point algebra, a fact that fails for general partial actions of finite Rokhlin dimension.
4.1 The decomposition property
An important ingredient in our study of partial actions with finite Rokhlin dimension is our previous work [Reference Abadie, Gardella and Geffen2] on decomposable partial actions. For the convenience of the reader, we make here a small digression.
Definition 4.1. Let G be a finite group. Given
![]() $n=1,\ldots ,|G|$
, we define the space of n-tuples of G to be
$n=1,\ldots ,|G|$
, we define the space of n-tuples of G to be
For
![]() $g\in G$
, we set
$g\in G$
, we set
![]() $\mathcal {T}_n(G)_{g}=\{\tau \in \mathcal {T}_n(G)\colon g\in \tau \}$
. There is a canonical partial action
$\mathcal {T}_n(G)_{g}=\{\tau \in \mathcal {T}_n(G)\colon g\in \tau \}$
. There is a canonical partial action
![]() $\texttt {Lt}$
of G on
$\texttt {Lt}$
of G on
![]() $\mathcal {T}_n(G)$
, with
$\mathcal {T}_n(G)$
, with
![]() $\texttt {Lt}_g\colon \mathcal {T}_n(G)_{g^{-1}}\to \mathcal {T}_n(G)_g$
induced by left translation by g. For
$\texttt {Lt}_g\colon \mathcal {T}_n(G)_{g^{-1}}\to \mathcal {T}_n(G)_g$
induced by left translation by g. For
![]() $\tau \in \mathcal {T}_n(G)$
, we write
$\tau \in \mathcal {T}_n(G)$
, we write
![]() $G\cdot \tau \subseteq \mathcal {T}_n(G)$
for the orbit of
$G\cdot \tau \subseteq \mathcal {T}_n(G)$
for the orbit of
![]() $\tau $
with respect to
$\tau $
with respect to
![]() $\texttt {Lt}$
.
$\texttt {Lt}$
.
We will adopt the following convention. Let
![]() $\alpha $
be a partial action of a finite group G on a
$\alpha $
be a partial action of a finite group G on a
![]() $C^*$
-algebra A, and let
$C^*$
-algebra A, and let
![]() $n=1,\ldots ,|G|$
. For
$n=1,\ldots ,|G|$
. For
![]() $\tau \in \mathcal {T}_n(G)$
, we write
$\tau \in \mathcal {T}_n(G)$
, we write
![]() $A_{\tau }$
for the ideal
$A_{\tau }$
for the ideal
![]() $A_{\tau }=\bigcap _{g\in \tau } A_{g}$
. Then
$A_{\tau }=\bigcap _{g\in \tau } A_{g}$
. Then
![]() $\alpha _{g}(A_{\tau })=A_{g\tau }$
for
$\alpha _{g}(A_{\tau })=A_{g\tau }$
for
![]() $g\in G$
and
$g\in G$
and
![]() $\tau \in \mathcal {T}_n(G)_{g^{-1}}$
. For
$\tau \in \mathcal {T}_n(G)_{g^{-1}}$
. For
![]() $\tau \in \mathcal {T}_n(G)$
, we set
$\tau \in \mathcal {T}_n(G)$
, we set
![]() $A_{G\cdot \tau }=\sum _{g\in \tau ^{-1}} A_{g\tau }$
. When
$A_{G\cdot \tau }=\sum _{g\in \tau ^{-1}} A_{g\tau }$
. When
![]() $A=C_0(X)$
for a locally compact Hausdorff space X, we write
$A=C_0(X)$
for a locally compact Hausdorff space X, we write
![]() $X_\tau $
for the spectrum of
$X_\tau $
for the spectrum of
![]() $C_0(X)_\tau $
, and identify it canonically with
$C_0(X)_\tau $
, and identify it canonically with
![]() $\bigcap _{g\in \tau }X_g$
. We use similar notation for
$\bigcap _{g\in \tau }X_g$
. We use similar notation for
![]() $X_{G\cdot \tau }$
.
$X_{G\cdot \tau }$
.
Definition 4.2. Let G be a finite group, let A be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha =((A_g)_{g\in G}, (\alpha _g)_{g\in G})$
be a partial action of G on A. Given
$\alpha =((A_g)_{g\in G}, (\alpha _g)_{g\in G})$
be a partial action of G on A. Given
![]() $n=1,\ldots ,|G|$
, we say that
$n=1,\ldots ,|G|$
, we say that
![]() $\alpha $
has the n-decomposition property if:
$\alpha $
has the n-decomposition property if:
-
(a)
 $A=\overline {\sum \nolimits _{\tau \in \mathcal {T}_n(G)}A_\tau }$
; and
$A=\overline {\sum \nolimits _{\tau \in \mathcal {T}_n(G)}A_\tau }$
; and -
(b)
 $A_{\tau }\cap A_g= \{0\}$
for all
$A_{\tau }\cap A_g= \{0\}$
for all
 $\tau \in \mathcal {T}_{n}(G)$
and all
$\tau \in \mathcal {T}_{n}(G)$
and all
 $g\in G$
such that
$g\in G$
such that
 $g\notin \tau $
.
$g\notin \tau $
.
We say that
![]() $\alpha $
is decomposable if it has the n-decomposition property for some
$\alpha $
is decomposable if it has the n-decomposition property for some
![]() $n\in {\mathbb {N}}$
. A partial action on a locally compact space X is said to have the n-decomposition property if the induced partial action on
$n\in {\mathbb {N}}$
. A partial action on a locally compact space X is said to have the n-decomposition property if the induced partial action on
![]() $C_0(X)$
has it.
$C_0(X)$
has it.
Notation 4.3. Adopt the notation from Definition 4.2. For
![]() $\tau \in \mathcal {T}_n(G)$
, we set
$\tau \in \mathcal {T}_n(G)$
, we set
![]() $H_\tau =\{h\in G\colon h\tau =\tau \}$
and
$H_\tau =\{h\in G\colon h\tau =\tau \}$
and
![]() $m_\tau =({n}/({|H_\tau |})) -1$
. Using Lemma 2.8 in [Reference Abadie, Gardella and Geffen2], we fix elements
$m_\tau =({n}/({|H_\tau |})) -1$
. Using Lemma 2.8 in [Reference Abadie, Gardella and Geffen2], we fix elements
![]() $x_0^\tau =1, x_1^\tau ,\ldots ,x_{m_\tau }^\tau \in G$
satisfying
$x_0^\tau =1, x_1^\tau ,\ldots ,x_{m_\tau }^\tau \in G$
satisfying
Whenever
![]() $\tau $
is understood from the context, we will omit it from the notation for
$\tau $
is understood from the context, we will omit it from the notation for
![]() $H_\tau $
,
$H_\tau $
,
![]() $m_\tau $
and
$m_\tau $
and
![]() $x_j^\tau $
, for
$x_j^\tau $
, for
![]() $j=1,\ldots ,m_\tau $
. Let
$j=1,\ldots ,m_\tau $
. Let
![]() $\mathcal {O}_n(G)$
be the orbit space for the partial system described in Definition 4.1. We denote by
$\mathcal {O}_n(G)$
be the orbit space for the partial system described in Definition 4.1. We denote by
![]() $\kappa \colon \mathcal {T}_n(G)\to \mathcal {O}_n(G)$
the canonical quotient map and fix, for the rest of this work, a global section
$\kappa \colon \mathcal {T}_n(G)\to \mathcal {O}_n(G)$
the canonical quotient map and fix, for the rest of this work, a global section
![]() $\eta \colon \mathcal {O}_n(G)\to \mathcal {T}_n(G)$
for it. For
$\eta \colon \mathcal {O}_n(G)\to \mathcal {T}_n(G)$
for it. For
![]() $z\in \mathcal {O}_n(G)$
, we write
$z\in \mathcal {O}_n(G)$
, we write
![]() $\tau _z$
for
$\tau _z$
for
![]() $\eta (z)$
,
$\eta (z)$
,
![]() $H_z$
for
$H_z$
for
![]() $H_{\tau _z}$
, and
$H_{\tau _z}$
, and
![]() $m_z$
for
$m_z$
for
![]() $m_{\tau _z}$
.
$m_{\tau _z}$
.
The following is part of Proposition 2.11 in [Reference Abadie, Gardella and Geffen2].
Proposition 4.4. Let G be a finite group, let A be a
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $n=1,\ldots ,|G|$
, let
$n=1,\ldots ,|G|$
, let
![]() $\alpha $
be a partial action of G on A with the n-decomposition property, and let
$\alpha $
be a partial action of G on A with the n-decomposition property, and let
![]() $\tau \in \mathcal {T}_n(G)$
. Adopt the conventions from Notation
4.3
. Then:
$\tau \in \mathcal {T}_n(G)$
. Adopt the conventions from Notation
4.3
. Then:
-
(1) the restriction of
 $\alpha |_{H_\tau }$
to
$\alpha |_{H_\tau }$
to
 $A_\tau $
is a global action;
$A_\tau $
is a global action; -
(2) there is a natural G-equivariant isomorphism
given by $$ \begin{align*}\varphi\colon \bigoplus_{z\in\mathcal{O}_n(G)} A_{G\cdot \tau_z} \to A\end{align*} $$
$$ \begin{align*}\varphi\colon \bigoplus_{z\in\mathcal{O}_n(G)} A_{G\cdot \tau_z} \to A\end{align*} $$
 $\varphi (a)=\sum _{z\in \mathcal {O}_n(G)} a_z$
for all
$\varphi (a)=\sum _{z\in \mathcal {O}_n(G)} a_z$
for all
 $a=(a_z)_{z\in \mathcal {O}_n(G)}$
.
$a=(a_z)_{z\in \mathcal {O}_n(G)}$
.
By part (2) above, many facts about decomposable partial actions can be reduced to the G-invariant direct summands
![]() $A_{G\cdot \tau }$
. In particular, for many purposes it suffices to work with a single
$A_{G\cdot \tau }$
. In particular, for many purposes it suffices to work with a single
![]() $\tau \in \mathcal {T}_n(G)$
and the induced partial action on
$\tau \in \mathcal {T}_n(G)$
and the induced partial action on
![]() $A_{G\cdot \tau }$
.
$A_{G\cdot \tau }$
.
Next, we recall Theorem 6.1 from [Reference Abadie, Gardella and Geffen2], which asserts that every partial action of a finite group is canonically an iterated extension of decomposable partial actions. It follows that many aspects of partial actions of finite groups can be reduced to the case of decomposable partial actions, as long as one has control over the resulting equivariant extension problem (which is in general quite complicated).
Theorem 4.5. Let G be a finite group, let A be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha $
be a partial action of G on A. Then there are canonical equivariant extensions
$\alpha $
be a partial action of G on A. Then there are canonical equivariant extensions
for
![]() $2\leq k \leq |G|$
, satisfying the following properties:
$2\leq k \leq |G|$
, satisfying the following properties:
-
(a)
 $A^{(|G|)}=A$
and
$A^{(|G|)}=A$
and
 $\alpha ^{|G|}=\alpha $
;
$\alpha ^{|G|}=\alpha $
; -
(b)
 $\delta ^{(k)}$
has the k-decomposition property;
$\delta ^{(k)}$
has the k-decomposition property; -
(c)
 $\alpha ^{(1)}$
has the 1-decomposition property.
$\alpha ^{(1)}$
has the 1-decomposition property.
We close this subsection by showing that the Rokhlin dimension of a decomposable partial action can be computed in terms of the global subsystems
![]() $H_\tau \curvearrowright A_{\tau }$
.
$H_\tau \curvearrowright A_{\tau }$
.
Theorem 4.6. Let G be a finite group, let A be a
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $n=1,\ldots ,|G|$
, and let
$n=1,\ldots ,|G|$
, and let
![]() $\alpha $
be a partial action of a finite group G on A with the n-decomposition property. Fix
$\alpha $
be a partial action of a finite group G on A with the n-decomposition property. Fix
![]() $\tau \in \mathcal {T}_n(G)$
. Then
$\tau \in \mathcal {T}_n(G)$
. Then
Consequently,
Proof We begin by observing that the last two identities are consequences of the first two, by part (2) of Proposition 4.4.
We give a proof for the first equality; the proof for
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is similar. We start by showing
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
is similar. We start by showing
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
. For this we set
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
. For this we set
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
and assume that
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
and assume that
![]() $d~<~\infty $
. Adopt Notation 4.3, and fix
$d~<~\infty $
. Adopt Notation 4.3, and fix
![]() $x_0=1,x_1,\ldots , x_m\in G$
with
$x_0=1,x_1,\ldots , x_m\in G$
with
Let
![]() $F\subseteq A_{G\cdot \tau }$
be a finite subset consisting of contractions, and let
$F\subseteq A_{G\cdot \tau }$
be a finite subset consisting of contractions, and let
![]() $\varepsilon>0$
. Since
$\varepsilon>0$
. Since
![]() $A_{G\cdot \tau }$
can be canonically identified with
$A_{G\cdot \tau }$
can be canonically identified with
![]() $\bigoplus _{\ell =0}^{m} A_{x_\ell ^{-1}\tau }$
, we may assume that F can be written as a disjoint union
$\bigoplus _{\ell =0}^{m} A_{x_\ell ^{-1}\tau }$
, we may assume that F can be written as a disjoint union
![]() $F=F_0\sqcup \cdots \sqcup F_m$
, where
$F=F_0\sqcup \cdots \sqcup F_m$
, where
![]() $F_\ell \subseteq A_{x_\ell ^{-1}\tau }$
for every
$F_\ell \subseteq A_{x_\ell ^{-1}\tau }$
for every
![]() $\ell =0,\ldots ,m$
. Set
$\ell =0,\ldots ,m$
. Set
![]() $K=\bigcup _{\ell =1}^m \alpha _{x_\ell }(F_\ell )\subseteq A_{\tau }$
, and let
$K=\bigcup _{\ell =1}^m \alpha _{x_\ell }(F_\ell )\subseteq A_{\tau }$
, and let
![]() $\xi _h^{(j)}\in A_\tau $
, for
$\xi _h^{(j)}\in A_\tau $
, for
![]() $h\in H_\tau $
and
$h\in H_\tau $
and
![]() $j=0,\ldots ,d$
, be Rokhlin towers for
$j=0,\ldots ,d$
, be Rokhlin towers for
![]() $\alpha |_{H_\tau }$
with respect to
$\alpha |_{H_\tau }$
with respect to
![]() $(K,\varepsilon )$
. (Note that
$(K,\varepsilon )$
. (Note that
![]() $\xi _h^{(j)}\neq 0$
for all
$\xi _h^{(j)}\neq 0$
for all
![]() $h\in H_\tau $
and all
$h\in H_\tau $
and all
![]() $j=0,\ldots ,d$
.) For
$j=0,\ldots ,d$
.) For
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, we set
$j=0,\ldots ,d$
, we set
 $$ \begin{align*}f_g^{(j)}=\begin{cases} \alpha_{x_\ell^{-1}}(\xi_h^{(j)}) & \text{if } g=x_\ell^{-1}h \text{ for some } \ell=0,\ldots, m \text{ and } h\in H_\tau,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
$$ \begin{align*}f_g^{(j)}=\begin{cases} \alpha_{x_\ell^{-1}}(\xi_h^{(j)}) & \text{if } g=x_\ell^{-1}h \text{ for some } \ell=0,\ldots, m \text{ and } h\in H_\tau,\\ 0 & \text{otherwise}. \end{cases} \end{align*} $$
Observe that
![]() $f_g^{(j)}$
is well defined (because
$f_g^{(j)}$
is well defined (because
![]() $x_\ell ^{-1}H_\tau \cap x_{r}^{-1}H_\tau =\emptyset $
if
$x_\ell ^{-1}H_\tau \cap x_{r}^{-1}H_\tau =\emptyset $
if
![]() $\ell \neq r$
) and that it is a positive contraction in
$\ell \neq r$
) and that it is a positive contraction in
![]() $A_{G\cdot \tau }\cap A_g$
. We claim that the
$A_{G\cdot \tau }\cap A_g$
. We claim that the
![]() $f_g^{(j)}$
satisfy the conditions in Definition 2.1 and thus witness the fact that
$f_g^{(j)}$
satisfy the conditions in Definition 2.1 and thus witness the fact that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
.
In order to check (1), let
![]() $g,k\in G$
,
$g,k\in G$
,
![]() $j=0,\ldots ,d$
, let
$j=0,\ldots ,d$
, let
![]() $\ell =0,\ldots ,m$
, and let
$\ell =0,\ldots ,m$
, and let
![]() $ x\in A_{g^{-1}}\cap F_\ell $
. We need to show that
$ x\in A_{g^{-1}}\cap F_\ell $
. We need to show that
Since by the decomposition property (specifically, condition (b) in Definition 4.2), the element
![]() $x\in A_{g^{-1}}\cap F_\ell $
is zero (and hence the inequality holds trivially) whenever
$x\in A_{g^{-1}}\cap F_\ell $
is zero (and hence the inequality holds trivially) whenever
![]() $g^{-1}\notin x_{\ell }^{-1}\tau $
, it suffices to assume that there exist unique
$g^{-1}\notin x_{\ell }^{-1}\tau $
, it suffices to assume that there exist unique
![]() $h\in H_\tau $
and
$h\in H_\tau $
and
![]() $r=0,\ldots ,m$
such that
$r=0,\ldots ,m$
such that
![]() $g=x_r^{-1}hx_\ell $
. By construction, we have
$g=x_r^{-1}hx_\ell $
. By construction, we have
![]() $f_k^{(j)}=0$
unless
$f_k^{(j)}=0$
unless
![]() $k\in \tau ^{-1}$
, and similarly
$k\in \tau ^{-1}$
, and similarly
![]() $f_{gk}^{(j)}=0$
unless
$f_{gk}^{(j)}=0$
unless
![]() $gk\in \tau ^{-1}$
. We accordingly divide the proof into three cases.
$gk\in \tau ^{-1}$
. We accordingly divide the proof into three cases.
Case 1.
![]() $k\notin \tau ^{-1}$
, so that
$k\notin \tau ^{-1}$
, so that
![]() $f_k^{(j)}=0$
. We claim that
$f_k^{(j)}=0$
. We claim that
![]() $f_{gk}^{(j)}\alpha _g(x)=0$
. Arguing by contradiction, assume that the product
$f_{gk}^{(j)}\alpha _g(x)=0$
. Arguing by contradiction, assume that the product
![]() $f_{gk}^{(j)}\alpha _g(x)$
, which belongs to
$f_{gk}^{(j)}\alpha _g(x)$
, which belongs to
![]() $A_{gk}\cap A_\tau $
, is non-zero. By the intersection property, we must have
$A_{gk}\cap A_\tau $
, is non-zero. By the intersection property, we must have
![]() $gk\in \tau $
and thus there are unique
$gk\in \tau $
and thus there are unique
![]() $s=0,\ldots ,m$
and
$s=0,\ldots ,m$
and
![]() $h_1\in H_\tau $
with
$h_1\in H_\tau $
with
![]() $gk=x_s^{-1}h_1$
. Since
$gk=x_s^{-1}h_1$
. Since
![]() $f_{gk}^{(j)}\alpha _g(x)$
, which belongs to
$f_{gk}^{(j)}\alpha _g(x)$
, which belongs to
![]() $A_{x_r^{-1}\tau }\cap A_{x_{s}^{-1}\tau }$
, is nonzero, the decomposition property implies that
$A_{x_r^{-1}\tau }\cap A_{x_{s}^{-1}\tau }$
, is nonzero, the decomposition property implies that
![]() $r=s$
. Thus
$r=s$
. Thus
contradicting our assumption. This verifies (4.1) in this case.
Case 2.
![]() $gk\notin \tau ^{-1}$
, so that
$gk\notin \tau ^{-1}$
, so that
![]() $f_{gk}^{(j)}=0$
. We claim that
$f_{gk}^{(j)}=0$
. We claim that
![]() $\alpha _g(f_k^{(j)}x)=0$
. Arguing by contradiction, assume that the product
$\alpha _g(f_k^{(j)}x)=0$
. Arguing by contradiction, assume that the product
![]() $f_k^{(j)}x$
, which belongs to
$f_k^{(j)}x$
, which belongs to
![]() $A_{k}\cap A_{x_\ell ^{-1}\tau }$
, is non-zero. By the intersection property, we must have
$A_{k}\cap A_{x_\ell ^{-1}\tau }$
, is non-zero. By the intersection property, we must have
![]() $k\in x_\ell ^{-1}\tau $
, and thus there is
$k\in x_\ell ^{-1}\tau $
, and thus there is
![]() $h_2\in H_\tau $
with
$h_2\in H_\tau $
with
![]() $k=x_\ell ^{-1}h_2$
. Thus
$k=x_\ell ^{-1}h_2$
. Thus
contradicting our assumption. This verifies (4.1) in this case.
Case 3.
![]() $gk,k \in \tau ^{-1}$
. Then there exists
$gk,k \in \tau ^{-1}$
. Then there exists
![]() $\widetilde {h}\in H_\tau $
with
$\widetilde {h}\in H_\tau $
with
![]() $k=x_\ell ^{-1}\widetilde {h}$
, so that
$k=x_\ell ^{-1}\widetilde {h}$
, so that
![]() $gk=x_{r}^{-1}h\widetilde {h}$
. Thus,
$gk=x_{r}^{-1}h\widetilde {h}$
. Thus,
 $$ \begin{align*} \| \alpha_g(f_k^{(j)}x)-f_{gk}^{(j)}\alpha_g(x)\| =\|\underbrace{\alpha_{x_r^{-1}hx_\ell}(\alpha_{x_\ell^{-1}}(\xi_{\widetilde{h}}^{(j)})x)}_{\approx_{\varepsilon}\ \alpha_{x_r^{-1}}(\xi_{h\widetilde{h}}^{(j)})\alpha_{g}(x)}-\alpha_{x_r^{-1}}(\xi_{h\widetilde{h}}^{(j)})\alpha_{g}(x)\| < \varepsilon, \end{align*} $$
$$ \begin{align*} \| \alpha_g(f_k^{(j)}x)-f_{gk}^{(j)}\alpha_g(x)\| =\|\underbrace{\alpha_{x_r^{-1}hx_\ell}(\alpha_{x_\ell^{-1}}(\xi_{\widetilde{h}}^{(j)})x)}_{\approx_{\varepsilon}\ \alpha_{x_r^{-1}}(\xi_{h\widetilde{h}}^{(j)})\alpha_{g}(x)}-\alpha_{x_r^{-1}}(\xi_{h\widetilde{h}}^{(j)})\alpha_{g}(x)\| < \varepsilon, \end{align*} $$
verifying (4.1) also in this case.
We turn to condition (2) in Definition 2.1 Let
![]() $g,k\in G$
with
$g,k\in G$
with
![]() $g\neq k$
, let
$g\neq k$
, let
![]() $j=0,\ldots ,d$
, let
$j=0,\ldots ,d$
, let
![]() $\ell =0,\ldots ,m$
, and let
$\ell =0,\ldots ,m$
, and let
![]() $a\in F_\ell $
. We need to show that
$a\in F_\ell $
. We need to show that
![]() $f_{g}^{(j)}f_k^{(j)}a$
has norm at most
$f_{g}^{(j)}f_k^{(j)}a$
has norm at most
![]() $\varepsilon $
. We may assume that there exist
$\varepsilon $
. We may assume that there exist
![]() $r,s=0,\ldots ,m$
and
$r,s=0,\ldots ,m$
and
![]() $h_1,h_2\in H_\tau $
with
$h_1,h_2\in H_\tau $
with
![]() $g=x_r^{-1}h_1$
and
$g=x_r^{-1}h_1$
and
![]() $k=x_s^{-1}h_2$
(or else either
$k=x_s^{-1}h_2$
(or else either
![]() $f_g^{(j)}=0$
or
$f_g^{(j)}=0$
or
![]() $f_k^{(j)}=0$
). Additionally, since the product
$f_k^{(j)}=0$
). Additionally, since the product
![]() $f_{g}^{(j)}f_k^{(j)}a$
belongs to
$f_{g}^{(j)}f_k^{(j)}a$
belongs to
![]() $A_{g}\cap A_k\cap A_{x_\ell ^{-1}\tau }$
, we may assume that
$A_{g}\cap A_k\cap A_{x_\ell ^{-1}\tau }$
, we may assume that
![]() $r=s=\ell $
(or else
$r=s=\ell $
(or else
![]() $f_{g}^{(j)}f_k^{(j)}a=0$
). In this case, we have
$f_{g}^{(j)}f_k^{(j)}a=0$
). In this case, we have
 $$ \begin{align*} f_{g}^{(j)}f_k^{(j)}a= \alpha_{x_\ell^{-1}}(\xi_{h_1}^{(j)})\alpha_{x_\ell^{-1}}(\xi_{h_2}^{(j)})a =\alpha_{x_\ell^{-1}}(\underbrace{\xi_{h_1}^{(j)}\xi_{h_2}^{(j)}\alpha_{x_\ell}(a)}_{\approx_{\varepsilon} \ 0})\approx_\varepsilon 0, \end{align*} $$
$$ \begin{align*} f_{g}^{(j)}f_k^{(j)}a= \alpha_{x_\ell^{-1}}(\xi_{h_1}^{(j)})\alpha_{x_\ell^{-1}}(\xi_{h_2}^{(j)})a =\alpha_{x_\ell^{-1}}(\underbrace{\xi_{h_1}^{(j)}\xi_{h_2}^{(j)}\alpha_{x_\ell}(a)}_{\approx_{\varepsilon} \ 0})\approx_\varepsilon 0, \end{align*} $$
as desired. In order to check condition (3), let
![]() $\ell =0,\ldots ,m$
and
$\ell =0,\ldots ,m$
and
![]() $a\in F_\ell $
. Using at the second step that a product of the form
$a\in F_\ell $
. Using at the second step that a product of the form
![]() $\alpha _{x_r^{-1}}(\xi _h^{(j)})a$
is zero unless
$\alpha _{x_r^{-1}}(\xi _h^{(j)})a$
is zero unless
![]() $r=\ell $
, we have
$r=\ell $
, we have
 $$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G} f_g^{(j)}a&=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{r=0}^{m} \alpha_{x_r^{-1}}(\xi_h^{(j)})a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\alpha_{x_\ell^{-1}}(\xi_h^{(j)})a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\alpha_{x_\ell^{-1}}(\xi_h^{(j)}\alpha_{x_\ell}(a))\\ &=\alpha_{x_{\ell}^{-1}}\bigg(\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\xi_h^{(j)}\alpha_{x_\ell}(a)\bigg)\approx_{\varepsilon} \alpha_{x_\ell}(a), \end{align*} $$
$$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{g\in G} f_g^{(j)}a&=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{r=0}^{m} \alpha_{x_r^{-1}}(\xi_h^{(j)})a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\alpha_{x_\ell^{-1}}(\xi_h^{(j)})a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\alpha_{x_\ell^{-1}}(\xi_h^{(j)}\alpha_{x_\ell}(a))\\ &=\alpha_{x_{\ell}^{-1}}\bigg(\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\xi_h^{(j)}\alpha_{x_\ell}(a)\bigg)\approx_{\varepsilon} \alpha_{x_\ell}(a), \end{align*} $$
as desired. Finally, to check condition (4), let
![]() $g\in G$
,
$g\in G$
,
![]() $j=0,\ldots ,d$
,
$j=0,\ldots ,d$
,
![]() $\ell =0,\ldots ,m$
, and
$\ell =0,\ldots ,m$
, and
![]() $a\in F_\ell $
be given. Since
$a\in F_\ell $
be given. Since
![]() $f_g^{(j)}=0$
unless
$f_g^{(j)}=0$
unless
![]() $g\in \tau ^{-1}$
, we may assume that there are
$g\in \tau ^{-1}$
, we may assume that there are
![]() $h\in H_\tau $
and
$h\in H_\tau $
and
![]() $s=0,\ldots ,m$
such that
$s=0,\ldots ,m$
such that
![]() $g=x_s^{-1}h$
. Since the products
$g=x_s^{-1}h$
. Since the products
![]() $f_g^{(j)}a$
and
$f_g^{(j)}a$
and
![]() $af_g^{(j)}$
are both zero unless
$af_g^{(j)}$
are both zero unless
![]() $g\in x_{\ell }^{-1}\tau $
, we may assume that
$g\in x_{\ell }^{-1}\tau $
, we may assume that
![]() $s=\ell $
. For
$s=\ell $
. For
![]() $b\in F$
, we have
$b\in F$
, we have
 $$ \begin{align*} \|(f_g^{(j)}a-af_g^{(j)})b\|&=\|(\alpha_{x_\ell^{-1}}(\xi_h^{(j)})a-a\alpha_{x_\ell^{-1}}(\xi_h^{(j)}))b\|\\ &=\|(\xi_h^{(j)}\alpha_{x_\ell}(a)-\alpha_{x_\ell}(a)\xi_h^{(j)})\alpha_{x_\ell}(b)\|<\varepsilon. \end{align*} $$
$$ \begin{align*} \|(f_g^{(j)}a-af_g^{(j)})b\|&=\|(\alpha_{x_\ell^{-1}}(\xi_h^{(j)})a-a\alpha_{x_\ell^{-1}}(\xi_h^{(j)}))b\|\\ &=\|(\xi_h^{(j)}\alpha_{x_\ell}(a)-\alpha_{x_\ell}(a)\xi_h^{(j)})\alpha_{x_\ell}(b)\|<\varepsilon. \end{align*} $$
This completes the proof that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })$
.
Next, we show
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})$
. Set
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})$
. Set
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})$
and assume that
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{A_{G\cdot \tau }})$
and assume that
![]() $d<\infty $
. Fix an approximate unit
$d<\infty $
. Fix an approximate unit
![]() $(e_{\lambda })_{\lambda \in \Lambda }$
of
$(e_{\lambda })_{\lambda \in \Lambda }$
of
![]() $A_\tau $
and let
$A_\tau $
and let
![]() $\pi \colon A_{G\cdot \tau }\to A_{\tau }$
be the quotient map given by
$\pi \colon A_{G\cdot \tau }\to A_{\tau }$
be the quotient map given by
![]() $\pi (x)=\lim _{\lambda }xe_\lambda $
for all
$\pi (x)=\lim _{\lambda }xe_\lambda $
for all
![]() $x\in A_{G\cdot \tau }$
. (The map
$x\in A_{G\cdot \tau }$
. (The map
![]() $\pi $
does not depend on the approximate identity, but this is not relevant to us.) Note that
$\pi $
does not depend on the approximate identity, but this is not relevant to us.) Note that
for all
![]() $x\in A_{G\cdot \tau }$
and all
$x\in A_{G\cdot \tau }$
and all
![]() $a\in A_\tau $
. Let
$a\in A_\tau $
. Let
![]() $F\subseteq A_\tau $
be a finite subset and let
$F\subseteq A_\tau $
be a finite subset and let
![]() $\varepsilon>0$
. We may assume without loss of generality that F is
$\varepsilon>0$
. We may assume without loss of generality that F is
![]() $H_\tau $
-invariant and consists of contractions. For every right coset
$H_\tau $
-invariant and consists of contractions. For every right coset
![]() $q\in H_\tau \setminus G$
, let
$q\in H_\tau \setminus G$
, let
![]() $g_q\in G$
satisfy
$g_q\in G$
satisfy
![]() $H_\tau g_q=q$
. Set
$H_\tau g_q=q$
. Set
![]() $\varepsilon _0={\varepsilon }/{[G:H_\tau ]^2}$
and let
$\varepsilon _0={\varepsilon }/{[G:H_\tau ]^2}$
and let
![]() $\xi _g^{(j)}\in A_{G\cdot \tau }\cap A_g$
, for
$\xi _g^{(j)}\in A_{G\cdot \tau }\cap A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots , d$
, be Rokhlin towers for
$j=0,\ldots , d$
, be Rokhlin towers for
![]() $\alpha |_{A_{G\cdot \tau }}$
with respect to
$\alpha |_{A_{G\cdot \tau }}$
with respect to
![]() $(F,\varepsilon _0)$
.
$(F,\varepsilon _0)$
.
For
![]() $h\in H_\tau $
and
$h\in H_\tau $
and
![]() $j=0,\ldots , d$
, we set
$j=0,\ldots , d$
, we set
 $$ \begin{align*}f_h^{(j)}= \sum\limits_{q\in H_\tau\setminus G}\pi(\xi^{(j)}_{hg_q})\in A_\tau. \end{align*} $$
$$ \begin{align*}f_h^{(j)}= \sum\limits_{q\in H_\tau\setminus G}\pi(\xi^{(j)}_{hg_q})\in A_\tau. \end{align*} $$
We claim that these positive contractions witness that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq d$
for
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq d$
for
![]() $(F,\varepsilon )$
.
$(F,\varepsilon )$
.
Let
![]() $h_1,h_2\in H_\tau $
, let
$h_1,h_2\in H_\tau $
, let
![]() $j=0,\ldots , d$
and let
$j=0,\ldots , d$
and let
![]() $a\in F$
be given. Then
$a\in F$
be given. Then
 $$ \begin{align*} \| \alpha_{h_1}(f_{h_2}^{(j)})a-f_{h_1h_2}a\|&\leq \sum\limits_{q\in H_\tau\setminus G}\| \alpha_{h_1}(\pi(\xi_{h_2g_q}^{(j)}))a-\xi_{h_1h_2g_q}^{(j)}a\|\\ &\stackrel{(4.2)}{=}\sum\limits_{q\in H_\tau\setminus G}\| \alpha_{h_1}(\xi_{h_2g_q}^{(j)}\alpha_{h_1^{-1}}(a))-\xi_{h_1h_2g_q}^{(j)}a\|\\ &\leq [G:H_\tau]\varepsilon_0\leq \varepsilon, \end{align*} $$
$$ \begin{align*} \| \alpha_{h_1}(f_{h_2}^{(j)})a-f_{h_1h_2}a\|&\leq \sum\limits_{q\in H_\tau\setminus G}\| \alpha_{h_1}(\pi(\xi_{h_2g_q}^{(j)}))a-\xi_{h_1h_2g_q}^{(j)}a\|\\ &\stackrel{(4.2)}{=}\sum\limits_{q\in H_\tau\setminus G}\| \alpha_{h_1}(\xi_{h_2g_q}^{(j)}\alpha_{h_1^{-1}}(a))-\xi_{h_1h_2g_q}^{(j)}a\|\\ &\leq [G:H_\tau]\varepsilon_0\leq \varepsilon, \end{align*} $$
thus establishing condition (1) in Definition 2.1. In order to prove (2), let
![]() $h_1,h_2\in H_\tau $
with
$h_1,h_2\in H_\tau $
with
![]() $h_1\neq h_2$
, let
$h_1\neq h_2$
, let
![]() $j=0,\ldots ,d$
, and let
$j=0,\ldots ,d$
, and let
![]() $a\in F$
. Then
$a\in F$
. Then
 $$ \begin{align*} \| f_{h_1}^{(j)}f_{h_2}^{(j)}a\|=\bigg\| \sum\limits_{p,q\in H_\tau\setminus G}\xi_{h_1g_q}^{(j)} \xi_{h_2g_p}^{(j)}a\bigg\| \leq [G:H_\tau]^2 \varepsilon_0=\varepsilon, \end{align*} $$
$$ \begin{align*} \| f_{h_1}^{(j)}f_{h_2}^{(j)}a\|=\bigg\| \sum\limits_{p,q\in H_\tau\setminus G}\xi_{h_1g_q}^{(j)} \xi_{h_2g_p}^{(j)}a\bigg\| \leq [G:H_\tau]^2 \varepsilon_0=\varepsilon, \end{align*} $$
using at the second step that
![]() $h_1g_q\neq h_2q_p$
for all
$h_1g_q\neq h_2q_p$
for all
![]() $p,q\in H_\tau \setminus G$
. To check (3), let
$p,q\in H_\tau \setminus G$
. To check (3), let
![]() $a\in F$
. Then
$a\in F$
. Then
 $$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}f_h^{(j)}a&= \sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{q\in H_\tau\setminus G}\pi(\xi_{hg_q}^{(j)})a\\ &\stackrel{(4.2)}{=}\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{q\in H_\tau\setminus G}\xi_{hg_q}^{(j)}a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\xi_{g}^{(j)}a\approx_\varepsilon a. \end{align*} $$
$$ \begin{align*} \sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}f_h^{(j)}a&= \sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{q\in H_\tau\setminus G}\pi(\xi_{hg_q}^{(j)})a\\ &\stackrel{(4.2)}{=}\sum\limits_{j=0}^{d}\sum\limits_{h\in H_\tau}\sum\limits_{q\in H_\tau\setminus G}\xi_{hg_q}^{(j)}a\\ &=\sum\limits_{j=0}^{d}\sum\limits_{g\in G}\xi_{g}^{(j)}a\approx_\varepsilon a. \end{align*} $$
Finally, to check (4), let
![]() $h\in H_\tau $
,
$h\in H_\tau $
,
![]() $j=0,\ldots , d$
, and
$j=0,\ldots , d$
, and
![]() $a,b\in F$
be given. Then
$a,b\in F$
be given. Then
 $$ \begin{align*} \|(f_h^{(j)}a-af_h^{(j)})b\|&=\bigg\| \sum\limits_{q\in H_\tau\setminus G}(\xi_{hg_q}^{(j)}a-a\xi_{hg_q}^{(j)})b\bigg\|\leq [G:H_\tau]\varepsilon_0\leq \varepsilon, \end{align*} $$
$$ \begin{align*} \|(f_h^{(j)}a-af_h^{(j)})b\|&=\bigg\| \sum\limits_{q\in H_\tau\setminus G}(\xi_{hg_q}^{(j)}a-a\xi_{hg_q}^{(j)})b\bigg\|\leq [G:H_\tau]\varepsilon_0\leq \varepsilon, \end{align*} $$
as required. This shows that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq d$
, and completes the proof.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_{H_\tau })\leq d$
, and completes the proof.
4.2 Crossed products and fixed point algebras
Our next result shows that a number of properties are preserved by formation of crossed products and fixed point algebras by partial actions with finite Rokhlin dimension. The kind of properties preserved in this setting are more restrictive than in the global setting, particularly since the properties in question must pass to extensions. For unital partial actions, we will show in Theorem 4.10 that even more properties are preserved.
Recall that if
![]() $\alpha $
is a partial action of a finite group G on a
$\alpha $
is a partial action of a finite group G on a
![]() $C^*$
-algebra A, then its crossed product
$C^*$
-algebra A, then its crossed product
![]() $A\rtimes _\alpha G$
is the set of all formal linear combinations of elements of the form
$A\rtimes _\alpha G$
is the set of all formal linear combinations of elements of the form
![]() $a_gu_g$
, where
$a_gu_g$
, where
![]() $g\in G$
and
$g\in G$
and
![]() $a_g\in A_g$
, subject to the relations
$a_g\in A_g$
, subject to the relations
We consider
![]() $A\rtimes _\alpha G$
with its greatest
$A\rtimes _\alpha G$
with its greatest
![]() $C^*$
-norm, which is not hard to see exists.
$C^*$
-norm, which is not hard to see exists.
Moreover, its fixed point algebra
![]() $A^\alpha $
is defined as
$A^\alpha $
is defined as
Theorem 4.7. Let G be a finite group, and let
![]() $d\in {\mathbb {N}}$
. Let P be a property for
$d\in {\mathbb {N}}$
. Let P be a property for
![]() $C^*$
-algebras which is preserved by:
$C^*$
-algebras which is preserved by:
-
(E) passage to ideals, quotients and extensions;
-
(M) Morita equivalence;
-
(C) crossed products by global actions of G with
 ${\mathrm {dim}_{\mathrm {Rok}}}\leq d$
.
${\mathrm {dim}_{\mathrm {Rok}}}\leq d$
.
Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha $
be a partial action of G on A. If
$\alpha $
be a partial action of G on A. If
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
and A satisfies P, then so do
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
and A satisfies P, then so do
![]() $A\rtimes _\alpha G$
and
$A\rtimes _\alpha G$
and
![]() $A^\alpha $
. In particular, the following hold.
$A^\alpha $
. In particular, the following hold.
-
(1) If
 ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
 ${\mathrm {dim}_{\mathrm {nuc}}}(A)<\infty $
, then
${\mathrm {dim}_{\mathrm {nuc}}}(A)<\infty $
, then
 ${\mathrm {dim}_{\mathrm {nuc}}}(A^\alpha ),{\mathrm {dim}_{\mathrm {nuc}}}(A\rtimes _\alpha G)<\infty $
. Indeed,
${\mathrm {dim}_{\mathrm {nuc}}}(A^\alpha ),{\mathrm {dim}_{\mathrm {nuc}}}(A\rtimes _\alpha G)<\infty $
. Indeed,  $$ \begin{align*}{\mathrm{dim}_{\mathrm{nuc}}}(A\rtimes_\alpha G)\leq (|G|-1)({\mathrm{dim}_{\mathrm{Rok}}}(\alpha)+1)({\mathrm{dim}_{\mathrm{nuc}}}(A)+1)+{\mathrm{dim}_{\mathrm{nuc}}}(A).\end{align*} $$
$$ \begin{align*}{\mathrm{dim}_{\mathrm{nuc}}}(A\rtimes_\alpha G)\leq (|G|-1)({\mathrm{dim}_{\mathrm{Rok}}}(\alpha)+1)({\mathrm{dim}_{\mathrm{nuc}}}(A)+1)+{\mathrm{dim}_{\mathrm{nuc}}}(A).\end{align*} $$
-
(2) If
 ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
 ${\mathrm {dr}}(A)<\infty $
, then
${\mathrm {dr}}(A)<\infty $
, then
 ${\mathrm {dr}}(A^\alpha ), {\mathrm {dr}}(A\rtimes _\alpha G)<\infty $
. Indeed,
${\mathrm {dr}}(A^\alpha ), {\mathrm {dr}}(A\rtimes _\alpha G)<\infty $
. Indeed,  $$ \begin{align*}{\mathrm{dr}}(A\rtimes_\alpha G)\leq (|G|-1)({\mathrm{dim}_{\mathrm{Rok}}}(\alpha)+1)({\mathrm{dr}}(A)+1)+{\mathrm{dr}}(A).\end{align*} $$
$$ \begin{align*}{\mathrm{dr}}(A\rtimes_\alpha G)\leq (|G|-1)({\mathrm{dim}_{\mathrm{Rok}}}(\alpha)+1)({\mathrm{dr}}(A)+1)+{\mathrm{dr}}(A).\end{align*} $$
A similar statement is true for
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. In particular, the following hold.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. In particular, the following hold.
-
(3) If
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
 $\mathrm {sr}(A)<\infty $
, then
$\mathrm {sr}(A)<\infty $
, then
 $\mathrm {sr}(A^\alpha ),\mathrm {sr}(A\rtimes _\alpha G)<\infty $
. Indeed,
$\mathrm {sr}(A^\alpha ),\mathrm {sr}(A\rtimes _\alpha G)<\infty $
. Indeed,  $$ \begin{align*}\mathrm{sr}(A\rtimes_\alpha G)\leq \frac{|G|({\mathrm{sr}}(A)+{\mathrm{dim}_{\mathrm{Rok}}^{\mathrm{c}}}(\alpha)+3)-2}{2}. \end{align*} $$
$$ \begin{align*}\mathrm{sr}(A\rtimes_\alpha G)\leq \frac{|G|({\mathrm{sr}}(A)+{\mathrm{dim}_{\mathrm{Rok}}^{\mathrm{c}}}(\alpha)+3)-2}{2}. \end{align*} $$
-
(4) If
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
 $\mathrm {RR}(A)<\infty $
, then
$\mathrm {RR}(A)<\infty $
, then
 $\mathrm {RR}(A^\alpha ),\mathrm {RR}(A\rtimes _\alpha G)<\infty $
.
$\mathrm {RR}(A^\alpha ),\mathrm {RR}(A\rtimes _\alpha G)<\infty $
. -
(5) Let
 $\mathcal {D}$
be a strongly self-absorbing
$\mathcal {D}$
be a strongly self-absorbing
 $C^*$
-algebra. If
$C^*$
-algebra. If
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and A is
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and A is
 $\mathcal {D}$
-absorbing, then
$\mathcal {D}$
-absorbing, then
 $A^\alpha $
and
$A^\alpha $
and
 $A\rtimes _\alpha G$
are
$A\rtimes _\alpha G$
are
 $\mathcal {D}$
-absorbing as well.
$\mathcal {D}$
-absorbing as well.
Proof Let P be a property as in the statement, let A be a
![]() $C^*$
-algebra satisfying P, and let
$C^*$
-algebra satisfying P, and let
![]() $\alpha $
be a partial action of G on A with
$\alpha $
be a partial action of G on A with
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
. By Theorem 4.5, there there are canonical equivariant extensions
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
. By Theorem 4.5, there there are canonical equivariant extensions
for
![]() $2\leq k \leq |G|$
, satisfying the following properties:
$2\leq k \leq |G|$
, satisfying the following properties:
-
(D.1)
 $A^{(|G|)}=A$
and
$A^{(|G|)}=A$
and
 $\alpha ^{|G|}=\alpha $
;
$\alpha ^{|G|}=\alpha $
; -
(D.2)
 $\delta ^{(k)}$
has the k-decomposition property;
$\delta ^{(k)}$
has the k-decomposition property; -
(D.3)
 $\alpha ^{(1)}$
has the 1-decomposition property.
$\alpha ^{(1)}$
has the 1-decomposition property.
In particular, each
![]() $A^{(k)}$
is a quotient of A, and each
$A^{(k)}$
is a quotient of A, and each
![]() $D^{(k)}$
is an ideal of a quotient of A. By (E), all of these
$D^{(k)}$
is an ideal of a quotient of A. By (E), all of these
![]() $C^*$
-algebras satisfy P. By repeatedly applying Proposition 2.6, we deduce that
$C^*$
-algebras satisfy P. By repeatedly applying Proposition 2.6, we deduce that
for all
![]() $k=2,\ldots ,|G|$
, while
$k=2,\ldots ,|G|$
, while
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^{(1)})=0$
by (D.3) and Example 2.2. For
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^{(1)})=0$
by (D.3) and Example 2.2. For
![]() $k=2,\ldots ,|G|$
, apply crossed products to (4.3) to get the extension
$k=2,\ldots ,|G|$
, apply crossed products to (4.3) to get the extension
Claim.
![]() $A^{(k)}\rtimes _{\alpha ^{(k)}} G$
satisfies P for all
$A^{(k)}\rtimes _{\alpha ^{(k)}} G$
satisfies P for all
![]() $k=1,\ldots ,|G|$
. We prove this by induction on k. Since
$k=1,\ldots ,|G|$
. We prove this by induction on k. Since
![]() $A^{(1)}\rtimes _{\alpha ^{(1)}} G=A^{(1)}$
by Example 2.2 and
$A^{(1)}\rtimes _{\alpha ^{(1)}} G=A^{(1)}$
by Example 2.2 and
![]() $A^{(1)}$
is a quotient of A, this follows from (E). Assume we have proved it for
$A^{(1)}$
is a quotient of A, this follows from (E). Assume we have proved it for
![]() $k-1$
, and let us prove it for k. Since P passes to extensions by (E), the exact sequence in (4.5) implies that it suffices to show that
$k-1$
, and let us prove it for k. Since P passes to extensions by (E), the exact sequence in (4.5) implies that it suffices to show that
![]() $D^{(k)}\rtimes _{\delta ^{(k)}} G$
satisfies P. Combining (D.2) and Theorem C in [Reference Abadie, Gardella and Geffen2], it follows that
$D^{(k)}\rtimes _{\delta ^{(k)}} G$
satisfies P. Combining (D.2) and Theorem C in [Reference Abadie, Gardella and Geffen2], it follows that
![]() $D^{(k)}\rtimes _{\delta ^{(k)}} G$
is isomorphic to a finite direct sum of algebras of the form
$D^{(k)}\rtimes _{\delta ^{(k)}} G$
is isomorphic to a finite direct sum of algebras of the form
![]() $M_{m_\tau }(D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau )$
, for
$M_{m_\tau }(D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau )$
, for
![]() $m_\tau =k/|H_\tau |\leq |G|$
and
$m_\tau =k/|H_\tau |\leq |G|$
and
![]() $\tau \in \mathcal {T}_k(G)$
, where
$\tau \in \mathcal {T}_k(G)$
, where
![]() $D^{(k)}_\tau $
is an ideal in
$D^{(k)}_\tau $
is an ideal in
![]() $D^{(k)}$
,
$D^{(k)}$
,
![]() $H_\tau $
is a subgroup of G, and
$H_\tau $
is a subgroup of G, and
![]() $\delta _\tau ^{(k)}$
is the global action obtained as the restriction of
$\delta _\tau ^{(k)}$
is the global action obtained as the restriction of
![]() $\delta ^{(k)}$
to
$\delta ^{(k)}$
to
![]() $H_\tau $
and to
$H_\tau $
and to
![]() $D^{(k)}_\tau $
. Thus, by (M) it suffices to show that
$D^{(k)}_\tau $
. Thus, by (M) it suffices to show that
![]() $D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau $
satisfies P for every
$D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau $
satisfies P for every
![]() $\tau \in \mathcal {T}_k(G)$
. Using Theorem 4.6 at the first step, we have
$\tau \in \mathcal {T}_k(G)$
. Using Theorem 4.6 at the first step, we have
Moreover,
![]() $D^{(k)}_\tau $
satisfies P by (E), since it is an ideal in
$D^{(k)}_\tau $
satisfies P by (E), since it is an ideal in
![]() $D^{(k)}$
. It follows from (C) that
$D^{(k)}$
. It follows from (C) that
![]() $D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau $
satisfies P, as desired. This proves the claim.
$D_\tau ^{(k)}\rtimes _{\delta _\tau ^{(k)}} H_\tau $
satisfies P, as desired. This proves the claim.
Since
![]() $A\rtimes _\alpha G$
equals
$A\rtimes _\alpha G$
equals
![]() $A^{(|G|)}\rtimes _{\alpha ^{(|G|)}} G$
by (D.1), this proves the first assertion in the theorem. Note that an identical argument applies to
$A^{(|G|)}\rtimes _{\alpha ^{(|G|)}} G$
by (D.1), this proves the first assertion in the theorem. Note that an identical argument applies to
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
in place of
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
in place of
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
. Moreover, the argument for fixed point algebras is analogous, by applying fixed point algebras to the extensions in (4.4), using Theorem 4.5 in [Reference Abadie, Gardella and Geffen2] instead of Theorem C there, and using the fact that fixed point algebras and crossed products are Morita equivalent in the global case. We omit the details.
${\mathrm {dim}_{\mathrm {Rok}}}$
. Moreover, the argument for fixed point algebras is analogous, by applying fixed point algebras to the extensions in (4.4), using Theorem 4.5 in [Reference Abadie, Gardella and Geffen2] instead of Theorem C there, and using the fact that fixed point algebras and crossed products are Morita equivalent in the global case. We omit the details.
The properties listed in conditions (1)–(5) are well known to satisfy (E) and (M); see [Reference Brown and Pedersen3, Reference Kirchberg and Winter20, Reference Rieffel22, Reference Winter and Zacharias25]. Finally, they also satisfy (C) by Corollary 4.25 in [Reference Gardella and Lupini14] and Theorem 3.20 in [Reference Gardella, Hirshberg and Santiago13].
For the estimates in (1), (2), and (3), one combines the estimates from Corollary 4.25 in [Reference Gardella and Lupini14] and Theorem 3.20 in [Reference Gardella, Hirshberg and Santiago13] with the known estimates for
![]() ${\mathrm {dim}_{\mathrm {nuc}}}$
,
${\mathrm {dim}_{\mathrm {nuc}}}$
,
![]() ${\mathrm {dr}}$
, or
${\mathrm {dr}}$
, or
![]() $\mathrm {sr}$
of an extension, or of
$\mathrm {sr}$
of an extension, or of
![]() $A\otimes M_n$
, and applies these a total of
$A\otimes M_n$
, and applies these a total of
![]() $|G|-1$
times to the extensions in (4.5). We omit the details.
$|G|-1$
times to the extensions in (4.5). We omit the details.
We note in passing that if
![]() $\alpha $
is a partial action of a finite group G on A, and A satisfies P, then
$\alpha $
is a partial action of a finite group G on A, and A satisfies P, then
![]() $A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
also satisfies P. Indeed, A is Morita equivalent to an ideal I of
$A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
also satisfies P. Indeed, A is Morita equivalent to an ideal I of
![]() $A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
whose linear orbit under the bidual action
$A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
whose linear orbit under the bidual action
![]() $\hat {\hat {\alpha }}$
is all of
$\hat {\hat {\alpha }}$
is all of
![]() $A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
([Reference Abadie1, Theorem 6.1]). Since P is preserved by Morita equivalence and by passage to ideals, quotients and extensions, then
$A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G$
([Reference Abadie1, Theorem 6.1]). Since P is preserved by Morita equivalence and by passage to ideals, quotients and extensions, then
![]() $\hat {\hat {\alpha }}_g(I)$
, and each sum
$\hat {\hat {\alpha }}_g(I)$
, and each sum
![]() $\hat {\hat {\alpha }}_g(I)+\hat {\hat {\alpha }}_{g'}(I)$
, also satisfy P. So
$\hat {\hat {\alpha }}_g(I)+\hat {\hat {\alpha }}_{g'}(I)$
, also satisfy P. So
![]() $A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G=\sum _{g\in G}\hat {\hat {\alpha }}_g(I)$
satisfies P.
$A\rtimes _\alpha G\rtimes _{\hat {\alpha }}G=\sum _{g\in G}\hat {\hat {\alpha }}_g(I)$
satisfies P.
The fact that the preservation results for
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $A\rtimes _\alpha G$
from Theorem 4.7 look identical suggests that there may be a tighter connection between these algebras. Indeed, in the global setting we have
$A\rtimes _\alpha G$
from Theorem 4.7 look identical suggests that there may be a tighter connection between these algebras. Indeed, in the global setting we have
![]() $A^\alpha \sim _M A\rtimes _\alpha G$
whenever G is abelian and
$A^\alpha \sim _M A\rtimes _\alpha G$
whenever G is abelian and
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
; see Corollary 1.18 in [Reference Gardella, Hirshberg and Santiago13]. The situation for partial actions is much more complicated, and there exist partial actions of finite groups with finite Rokhlin dimension such that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
; see Corollary 1.18 in [Reference Gardella, Hirshberg and Santiago13]. The situation for partial actions is much more complicated, and there exist partial actions of finite groups with finite Rokhlin dimension such that
![]() $A^\alpha $
is not Morita equivalent to
$A^\alpha $
is not Morita equivalent to
![]() $A\rtimes _\alpha G$
.
$A\rtimes _\alpha G$
.
Example 4.8. Set
![]() $X=(0,2]$
and
$X=(0,2]$
and
![]() $U=(0,1)\cup (1,2)\subseteq X$
, and let
$U=(0,1)\cup (1,2)\subseteq X$
, and let
![]() $\sigma \in \mathrm {Homeo}(U)$
be given by
$\sigma \in \mathrm {Homeo}(U)$
be given by
![]() $\sigma (x)=x+1 \, \mathrm {mod}\, 2$
for all
$\sigma (x)=x+1 \, \mathrm {mod}\, 2$
for all
![]() $x\in U$
. Let
$x\in U$
. Let
![]() $\alpha $
be the partial action of
$\alpha $
be the partial action of
![]() $G={\mathbb {Z}}_2=\{-1,1\}$
on
$G={\mathbb {Z}}_2=\{-1,1\}$
on
![]() $A=C_0(X)$
induced by
$A=C_0(X)$
induced by
![]() $\sigma $
. This action is considered in Example 5.2 of [Reference Abadie, Gardella and Geffen2], where it is shown that
$\sigma $
. This action is considered in Example 5.2 of [Reference Abadie, Gardella and Geffen2], where it is shown that
![]() $C_0(X)^{{\mathbb {Z}}_2}$
is not Morita equivalent to
$C_0(X)^{{\mathbb {Z}}_2}$
is not Morita equivalent to
![]() $C_0(X)\rtimes _\alpha {\mathbb {Z}}_2$
.
$C_0(X)\rtimes _\alpha {\mathbb {Z}}_2$
.
We claim that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
. Let
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
. Let
![]() $F\subseteq C_0(X)$
be a finite set, and let
$F\subseteq C_0(X)$
be a finite set, and let
![]() $\varepsilon>0$
. For
$\varepsilon>0$
. For
![]() $\delta>0$
, let
$\delta>0$
, let
![]() $f_\delta \in C_0(X)$
and
$f_\delta \in C_0(X)$
and
![]() $e_\delta \in C_0(U)$
be given by
$e_\delta \in C_0(U)$
be given by
 $$ \begin{align*} f_\delta(x)&=\begin{cases} 1 & \mbox{if }x\geq \delta, \\ \mathrm{linear} & \mathrm{otherwise} \end{cases} \quad \mbox{and}\\ e_\delta(x)&=\begin{cases} 1 & \mbox{if }x\in [\delta,1-\delta]\cup [1+\delta,2-\delta], \\ \mathrm{linear} & \mathrm{otherwise}. \end{cases}\end{align*} $$
$$ \begin{align*} f_\delta(x)&=\begin{cases} 1 & \mbox{if }x\geq \delta, \\ \mathrm{linear} & \mathrm{otherwise} \end{cases} \quad \mbox{and}\\ e_\delta(x)&=\begin{cases} 1 & \mbox{if }x\in [\delta,1-\delta]\cup [1+\delta,2-\delta], \\ \mathrm{linear} & \mathrm{otherwise}. \end{cases}\end{align*} $$
Find
![]() $\delta \in (0,1/4)$
such that
$\delta \in (0,1/4)$
such that
![]() $\|e_\delta a-a\|<\varepsilon $
for all
$\|e_\delta a-a\|<\varepsilon $
for all
![]() $a\in F\cap C_0(U)$
and
$a\in F\cap C_0(U)$
and
![]() $\|f_\delta a-a\|<\varepsilon $
for all
$\|f_\delta a-a\|<\varepsilon $
for all
![]() $a\in F$
. Set
$a\in F$
. Set
It is easy to check that the above positive contractions are Rokhlin towers for
![]() $(F,\varepsilon )$
, thus showing that
$(F,\varepsilon )$
, thus showing that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq 1$
, as desired. (In fact, one can also show that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq 1$
, as desired. (In fact, one can also show that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\neq 0$
, so that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\neq 0$
, so that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
is actually 1.)
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
is actually 1.)
4.3 Unital partial actions
For unital partial actions, a different approach can be used to obtain information about the crossed product, leading to a result which is stronger than Theorem 4.7, in that here we only demand that the property in question pass to direct sums and summands, as opposed to general extensions and ideals; see Theorem 4.10. Most significantly, this implies that the UCT is preserved in this setting; note that the UCT is not in general known to pass to ideals or quotients and hence does not satisfy condition (E) in Theorem 4.7. The same applies to several properties of the K-theory. Additionally, we isolate the case of Rokhlin dimension zero, for which considerably more can be said with this approach.
In contrast to Example 4.8, we show next that
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $A\rtimes _\alpha G$
are always Morita equivalent whenever
$A\rtimes _\alpha G$
are always Morita equivalent whenever
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
and
![]() $\alpha $
is unital. Our proof is very different from the arguments used in [Reference Gardella, Hirshberg and Santiago13] and has the advantage of being applicable to global actions of groups that are not necessarily abelian, thus obtaining new information even in the global setting.
$\alpha $
is unital. Our proof is very different from the arguments used in [Reference Gardella, Hirshberg and Santiago13] and has the advantage of being applicable to global actions of groups that are not necessarily abelian, thus obtaining new information even in the global setting.
In the next proof, for
![]() $\xi \in A\rtimes _\alpha G$
we write
$\xi \in A\rtimes _\alpha G$
we write
![]() $\xi (g)\in A_g$
,
$\xi (g)\in A_g$
,
![]() $g\in G$
, for the coefficient of
$g\in G$
, for the coefficient of
![]() $u_g$
in
$u_g$
in
![]() $\xi $
, so that
$\xi $
, so that
![]() $\xi =\sum _{g\in G}\xi (g)u_g$
.
$\xi =\sum _{g\in G}\xi (g)u_g$
.
Theorem 4.9. Let
![]() $\alpha $
be a unital partial action of a finite group G on a
$\alpha $
be a unital partial action of a finite group G on a
![]() $C^*$
-algebra A with
$C^*$
-algebra A with
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
. Then
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
. Then
![]() $A^\alpha $
is Morita equivalent to
$A^\alpha $
is Morita equivalent to
![]() $A\rtimes _\alpha G$
.
$A\rtimes _\alpha G$
.
Proof Set
![]() $x_\alpha =\sum _{g\in G}1_g$
. Then
$x_\alpha =\sum _{g\in G}1_g$
. Then
![]() $x_\alpha $
is central and positive, and since
$x_\alpha $
is central and positive, and since
![]() $x_\alpha \geq 1$
, it is invertible. Moreover,
$x_\alpha \geq 1$
, it is invertible. Moreover,
![]() $x_\alpha $
belongs to
$x_\alpha $
belongs to
![]() $A^\alpha $
, since for
$A^\alpha $
, since for
![]() $h\in G$
we have
$h\in G$
we have
 $$ \begin{align*}\alpha_h(x_\alpha 1_{h^{-1}})=\sum_{g\in G}\alpha_h(1_g1_{h^{-1}})= \sum_{g\in G} 1_{hg}1_h=x_\alpha 1_h, \end{align*} $$
$$ \begin{align*}\alpha_h(x_\alpha 1_{h^{-1}})=\sum_{g\in G}\alpha_h(1_g1_{h^{-1}})= \sum_{g\in G} 1_{hg}1_h=x_\alpha 1_h, \end{align*} $$
where at the second step we used Remark 2.3. We define a Hilbert
![]() $A^\alpha $
-
$A^\alpha $
-
![]() $A\rtimes _{\alpha } G$
-bimodule structure on A as follows. For
$A\rtimes _{\alpha } G$
-bimodule structure on A as follows. For
![]() $a\in A^\alpha $
,
$a\in A^\alpha $
,
![]() $x\in A$
and
$x\in A$
and
![]() $\xi \in A\rtimes _{\alpha }G$
, set
$\xi \in A\rtimes _{\alpha }G$
, set
![]() $a\cdot x=ax$
(the product is taken in A) and
$a\cdot x=ax$
(the product is taken in A) and
![]() $x\cdot \xi = \sum \nolimits _{g\in G} \alpha _{g^{-1}}(x\xi (g))$
. The inner products are given by
$x\cdot \xi = \sum \nolimits _{g\in G} \alpha _{g^{-1}}(x\xi (g))$
. The inner products are given by
 $$ \begin{align*}_{A^\alpha}\langle{x,y}\rangle = \sum\limits_{g\in G}\alpha_g(xy^*1_{g^{-1}}) \quad \mbox{and} \quad \langle{x,y}\rangle_{A\rtimes_{\alpha}G}=\sum\limits_{g\in G} x^*\alpha_g(y1_{g^{-1}})u_g\end{align*} $$
$$ \begin{align*}_{A^\alpha}\langle{x,y}\rangle = \sum\limits_{g\in G}\alpha_g(xy^*1_{g^{-1}}) \quad \mbox{and} \quad \langle{x,y}\rangle_{A\rtimes_{\alpha}G}=\sum\limits_{g\in G} x^*\alpha_g(y1_{g^{-1}})u_g\end{align*} $$
for
![]() $a\in A^\alpha $
,
$a\in A^\alpha $
,
![]() $x,y\in A$
and
$x,y\in A$
and
![]() $\xi \in A\rtimes _\alpha G$
. (One readily checks that
$\xi \in A\rtimes _\alpha G$
. (One readily checks that
![]() $_{A^\alpha }\langle {x,y}\rangle $
belongs to
$_{A^\alpha }\langle {x,y}\rangle $
belongs to
![]() $A^\alpha $
.) The properties of the inner products are easily verified. For example, for
$A^\alpha $
.) The properties of the inner products are easily verified. For example, for
![]() $x\in A$
we have
$x\in A$
we have
 $$ \begin{align*}x_\alpha\sum\limits_{g\in G}x^*\alpha_g(x1_{g^{-1}})u_g=\bigg(\sum\limits_{g\in G}\alpha_{g}(x1_{g^{-1}})u_g\bigg)^*\bigg(\sum\limits_{g\in G}\alpha_{g}(x1_{g^{-1}})u_g\bigg)\geq 0, \end{align*} $$
$$ \begin{align*}x_\alpha\sum\limits_{g\in G}x^*\alpha_g(x1_{g^{-1}})u_g=\bigg(\sum\limits_{g\in G}\alpha_{g}(x1_{g^{-1}})u_g\bigg)^*\bigg(\sum\limits_{g\in G}\alpha_{g}(x1_{g^{-1}})u_g\bigg)\geq 0, \end{align*} $$
so
![]() $\langle {x,x}\rangle _{A\rtimes _{\alpha }G}=\sum \nolimits _{g\in G}x^*\alpha _g(x1_{g^{-1}})u_g\geq 0$
, with equality exactly when
$\langle {x,x}\rangle _{A\rtimes _{\alpha }G}=\sum \nolimits _{g\in G}x^*\alpha _g(x1_{g^{-1}})u_g\geq 0$
, with equality exactly when
![]() $x=0$
. One can also easily check the properties of a bimodule. For example, given
$x=0$
. One can also easily check the properties of a bimodule. For example, given
![]() $\xi \in A\rtimes _\alpha G$
and
$\xi \in A\rtimes _\alpha G$
and
![]() $x,y\in A$
, we have
$x,y\in A$
, we have
 $$ \begin{align*}\langle{x,y}\rangle_{A\rtimes_{\alpha}G}\cdot \xi&=\sum\limits_{g\in G} x^*\alpha_g(y1_{g^{-1}})u_g\sum\limits_{h\in G}\xi(h)u_h\\ &=\sum\limits_{g,h\in G}\alpha_g(\alpha_{g^{-1}}(x^*\alpha_g(y1_{g^{-1}}))\xi(h))u_{gh}\\ &= \sum\limits_{g,h\in G}\alpha_g(\alpha_{g^{-1}}(x^*1_g)y\xi(h))u_{gh}\\ &=\sum\limits_{g,h\in G}x^*\alpha_g(y\xi(h)1_{g^{-1}})u_{gh}\\ &=\sum\limits_{g,h\in G}x^*\alpha_{gh^{-1}}(y\xi(h)1_{hg^{-1}})u_{g}\\ &= \sum\limits_{g,h \in G} x^*\alpha_g(\alpha_{h^{-1}}(y\xi(h))1_{g^{-1}})u_g\\ &= \langle{x,y\cdot \xi}\rangle_{A\rtimes_{\alpha}G}.\end{align*} $$
$$ \begin{align*}\langle{x,y}\rangle_{A\rtimes_{\alpha}G}\cdot \xi&=\sum\limits_{g\in G} x^*\alpha_g(y1_{g^{-1}})u_g\sum\limits_{h\in G}\xi(h)u_h\\ &=\sum\limits_{g,h\in G}\alpha_g(\alpha_{g^{-1}}(x^*\alpha_g(y1_{g^{-1}}))\xi(h))u_{gh}\\ &= \sum\limits_{g,h\in G}\alpha_g(\alpha_{g^{-1}}(x^*1_g)y\xi(h))u_{gh}\\ &=\sum\limits_{g,h\in G}x^*\alpha_g(y\xi(h)1_{g^{-1}})u_{gh}\\ &=\sum\limits_{g,h\in G}x^*\alpha_{gh^{-1}}(y\xi(h)1_{hg^{-1}})u_{g}\\ &= \sum\limits_{g,h \in G} x^*\alpha_g(\alpha_{h^{-1}}(y\xi(h))1_{g^{-1}})u_g\\ &= \langle{x,y\cdot \xi}\rangle_{A\rtimes_{\alpha}G}.\end{align*} $$
The other properties can be shown similarly. Moreover, for
![]() $x\in A^\alpha $
, we have
$x\in A^\alpha $
, we have
In particular, A is a full left
![]() $A^\alpha $
-module. Finally, we claim that A is a full right
$A^\alpha $
-module. Finally, we claim that A is a full right
![]() $A\rtimes _{\alpha }G$
-module. For this, it suffices to show that given
$A\rtimes _{\alpha }G$
-module. For this, it suffices to show that given
![]() $t\in G$
,
$t\in G$
,
![]() $x\in A_t$
and
$x\in A_t$
and
![]() $\varepsilon>0$
, there exist
$\varepsilon>0$
, there exist
![]() $k~\in ~{\mathbb {N}}$
and
$k~\in ~{\mathbb {N}}$
and
![]() $a_1,b_1,\ldots , a_k, b_k\in A$
such that
$a_1,b_1,\ldots , a_k, b_k\in A$
such that
![]() $xu_t\approx _\varepsilon \sum \nolimits _{\ell =1}^{k}\langle {a_\ell ,b_\ell }\rangle _{A\rtimes _{\alpha }G}$
. Set
$xu_t\approx _\varepsilon \sum \nolimits _{\ell =1}^{k}\langle {a_\ell ,b_\ell }\rangle _{A\rtimes _{\alpha }G}$
. Set
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
and
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
and
![]() $\varepsilon _0=\varepsilon /2(d+1)|G|$
, and use Proposition 2.4 to find
$\varepsilon _0=\varepsilon /2(d+1)|G|$
, and use Proposition 2.4 to find
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying:
$j=0,\ldots ,d$
, satisfying:
-
(a)
 $\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_g$
for all
$\alpha _g(f_h^{(j)}1_{g^{-1}})=f_{gh}^{(j)}1_g$
for all
 $g,h\in G$
;
$g,h\in G$
; -
(b)
 $f_g^{(j)}f_h^{(j)}\approx _{\varepsilon _0} 0$
for all
$f_g^{(j)}f_h^{(j)}\approx _{\varepsilon _0} 0$
for all
 $j=0,\ldots ,d$
and all distinct
$j=0,\ldots ,d$
and all distinct
 $g,h\in G$
;
$g,h\in G$
; -
(c)
 $\sum _{g\in G}\sum _{j=0}^d f_g^{(j)}\approx _{\varepsilon _0}1$
.
$\sum _{g\in G}\sum _{j=0}^d f_g^{(j)}\approx _{\varepsilon _0}1$
.
Using at the last step that
![]() $x\in A_t$
, we get
$x\in A_t$
, we get
 $$ \begin{align*} \sum_{g\in G}\sum_{j=0}^d\langle{{f_{tg}^{(j)}}^{{1}/{2}}x^*,{f_g^{(j)}}^{{1}/{2}}}\rangle_{A\rtimes_{\alpha}G} &=\sum_{g,h\in G}\sum_{j=0}^d x{f_{tg}^{(j)}}^{{1}/{2}}\alpha_h({f_g^{(j)}}^{{1}/{2}}1_{h^{-1}})u_h\\[-1pt] &\stackrel{\mathrm{(a)}}{=}\sum_{g,h\in G}\sum_{j=0}^d x{f_{tg}^{(j)}}^{{1}/{2}}{f_{hg}^{(j)}}^{{1}/{2}}1_hu_h\\[-1pt] &\stackrel{\mathrm{(b)}}{\approx}_{{\varepsilon}/{2}}\sum_{g\in G}\sum_{j=0}^d xf_{tg}^{(j)}1_tu_t\\[-1pt] &\stackrel{\mathrm{(c)}}{\approx}_{\varepsilon_0} x1_tu_t=xu_t, \end{align*} $$
$$ \begin{align*} \sum_{g\in G}\sum_{j=0}^d\langle{{f_{tg}^{(j)}}^{{1}/{2}}x^*,{f_g^{(j)}}^{{1}/{2}}}\rangle_{A\rtimes_{\alpha}G} &=\sum_{g,h\in G}\sum_{j=0}^d x{f_{tg}^{(j)}}^{{1}/{2}}\alpha_h({f_g^{(j)}}^{{1}/{2}}1_{h^{-1}})u_h\\[-1pt] &\stackrel{\mathrm{(a)}}{=}\sum_{g,h\in G}\sum_{j=0}^d x{f_{tg}^{(j)}}^{{1}/{2}}{f_{hg}^{(j)}}^{{1}/{2}}1_hu_h\\[-1pt] &\stackrel{\mathrm{(b)}}{\approx}_{{\varepsilon}/{2}}\sum_{g\in G}\sum_{j=0}^d xf_{tg}^{(j)}1_tu_t\\[-1pt] &\stackrel{\mathrm{(c)}}{\approx}_{\varepsilon_0} x1_tu_t=xu_t, \end{align*} $$
as desired. We conclude that A is an
![]() $A^\alpha $
-
$A^\alpha $
-
![]() $A\rtimes _{\alpha }G$
-imprimitivity bimodule, so these
$A\rtimes _{\alpha }G$
-imprimitivity bimodule, so these
![]() $C^*$
-algebras are Morita equivalent, and the proof is complete.
$C^*$
-algebras are Morita equivalent, and the proof is complete.
Theorem 4.10. Let G be a finite group, and let
![]() $d\in {\mathbb {N}}$
. Let P be a property for
$d\in {\mathbb {N}}$
. Let P be a property for
![]() $C^*$
-algebras which is preserved by:
$C^*$
-algebras which is preserved by:
-
(S) passage to direct sums and summands;
-
(M) Morita equivalence;
-
(C) crossed products by global actions of G with
 ${\mathrm {dim}_{\mathrm {Rok}}}\leq d$
.
${\mathrm {dim}_{\mathrm {Rok}}}\leq d$
.
Let A be a unital
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha $
be a unital partial action of G on A. If
$\alpha $
be a unital partial action of G on A. If
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
and A satisfies P, then so do
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
and A satisfies P, then so do
![]() $A\rtimes _\alpha G$
and
$A\rtimes _\alpha G$
and
![]() $A^\alpha $
. A similar statement is true if
$A^\alpha $
. A similar statement is true if
![]() ${\mathrm {dim}_{\mathrm {Rok}}}$
is replaced everywhere by
${\mathrm {dim}_{\mathrm {Rok}}}$
is replaced everywhere by
![]() ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. In particular, the following hold.
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}$
. In particular, the following hold.
-
(1) If
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and A satisfies the UCT, then so do
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and A satisfies the UCT, then so do
 $A\rtimes _\alpha G$
and
$A\rtimes _\alpha G$
and
 $A^\alpha $
.
$A^\alpha $
. -
(2) If
 ${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
${\mathrm {dim}_{\mathrm {Rok}}^{\mathrm {c}}}(\alpha )<\infty $
and
 $K_\ast (A)$
is either trivial, free, torsion-free, or finitely generated, then the same holds for
$K_\ast (A)$
is either trivial, free, torsion-free, or finitely generated, then the same holds for
 $A\rtimes _\alpha G$
and
$A\rtimes _\alpha G$
and
 $A^\alpha $
.
$A^\alpha $
.
When
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )=0$
, it follows that the properties listed in the main theorem of [Reference Gardella8] pass from A to
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )=0$
, it follows that the properties listed in the main theorem of [Reference Gardella8] pass from A to
![]() $A^\alpha $
and
$A^\alpha $
and
![]() $A\rtimes _\alpha G$
. This includes having real rank zero, having stable rank one, being an AF/approximately interval (AI)/approximately circle (A
$A\rtimes _\alpha G$
. This includes having real rank zero, having stable rank one, being an AF/approximately interval (AI)/approximately circle (A
![]() $\mathbb{T}$
)-algebra, being purely infinite, the order on projections being determined by traces, being weakly semiprojective, and having K-groups which are either trivial, free, torsion-free, or finitely generated.
$\mathbb{T}$
)-algebra, being purely infinite, the order on projections being determined by traces, being weakly semiprojective, and having K-groups which are either trivial, free, torsion-free, or finitely generated.
Proof By Theorem 4.9 and condition (M), it suffices to show the result for
![]() $A\rtimes _\alpha G$
. Let
$A\rtimes _\alpha G$
. Let
![]() $(B,\beta )$
denote the globalization of
$(B,\beta )$
denote the globalization of
![]() $(A,\alpha )$
.
$(A,\alpha )$
.
Claim.
There exist central projections
![]() $p_1,\ldots , p_{|G|}\in A$
such that
$p_1,\ldots , p_{|G|}\in A$
such that
![]() $B\cong p_1A\oplus \cdots \oplus p_{|G|}A$
. Since A is a unital ideal in B and
$B\cong p_1A\oplus \cdots \oplus p_{|G|}A$
. Since A is a unital ideal in B and
![]() $B=\sum _{g\in G}\beta _g(A)$
, it suffices to show the following: if
$B=\sum _{g\in G}\beta _g(A)$
, it suffices to show the following: if
![]() $I,J$
are unital ideals in a
$I,J$
are unital ideals in a
![]() $C^*$
-algebra, then
$C^*$
-algebra, then
![]() $I+J\cong pI\oplus J$
for some central projection
$I+J\cong pI\oplus J$
for some central projection
![]() $p\in I$
. This follows by taking
$p\in I$
. This follows by taking
![]() $p=1_I-1_I1_J$
and letting
$p=1_I-1_I1_J$
and letting
![]() $\psi \colon I+J\to pI\oplus J$
be
$\psi \colon I+J\to pI\oplus J$
be
![]() $\psi (x)=(px,1_Jx)$
for all
$\psi (x)=(px,1_Jx)$
for all
![]() $x\in I+J$
. We omit the easy details.
$x\in I+J$
. We omit the easy details.
Assume that A satisfies P and that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
. By the claim above and (S), it follows that B satisfies P. By Theorem 3.4, we have
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
. By the claim above and (S), it follows that B satisfies P. By Theorem 3.4, we have
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, and hence by (C) the global crossed product
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
, and hence by (C) the global crossed product
![]() $B\rtimes _\beta G$
satisfies P. Finally, since
$B\rtimes _\beta G$
satisfies P. Finally, since
![]() $B\rtimes _\beta G\sim _M A\rtimes _\alpha G$
by Theorem 4.18 in [Reference Abadie, Gardella and Geffen2], the result follows from (M).
$B\rtimes _\beta G\sim _M A\rtimes _\alpha G$
by Theorem 4.18 in [Reference Abadie, Gardella and Geffen2], the result follows from (M).
For the properties listed in (1) and (2), the preservation conditions (S) and (M) are well-known, while (C) is part of Theorem 3.20 in [Reference Gardella, Hirshberg and Santiago13]. The properties mentioned in the last part of the statement are also known to satisfy (S) and (M), and for
![]() $d=0$
they also satisfy (C) by the main result in [Reference Gardella8].
$d=0$
they also satisfy (C) by the main result in [Reference Gardella8].
Remark 4.11. In the context of the above theorem, one can obtain bounds for
![]() ${\mathrm {dim}_{\mathrm {nuc}}}$
,
${\mathrm {dim}_{\mathrm {nuc}}}$
,
![]() ${\mathrm {dr}}$
,
${\mathrm {dr}}$
,
![]() $\mathrm {sr}$
, and
$\mathrm {sr}$
, and
![]() $\mathrm {RR}$
of
$\mathrm {RR}$
of
![]() $A\rtimes _\alpha G$
and
$A\rtimes _\alpha G$
and
![]() $A^\alpha $
that are much better than the ones in Theorem 4.7, particularly since they do not depend on the cardinality of G. For example, one gets
$A^\alpha $
that are much better than the ones in Theorem 4.7, particularly since they do not depend on the cardinality of G. For example, one gets
![]() ${\mathrm {dim}_{\mathrm {nuc}}}(A\rtimes _\alpha G)\leq ({\mathrm {dim}_{\mathrm {Rok}}}(\alpha )+1)({\mathrm {dim}_{\mathrm {nuc}}}(A)+1)-1$
.
${\mathrm {dim}_{\mathrm {nuc}}}(A\rtimes _\alpha G)\leq ({\mathrm {dim}_{\mathrm {Rok}}}(\alpha )+1)({\mathrm {dim}_{\mathrm {nuc}}}(A)+1)-1$
.
5 Topological partial actions
In this section, we study the Rokhlin dimension of topological partial actions. In Theorem 5.10, we will show that a topological partial action
![]() $G\curvearrowright X$
on a finite-dimensional space X has finite Rokhlin dimension if and only if it is free. The case of global actions is implicit in [Reference Hirshberg and Phillips17], and it is an easy consequence of the existence of local cross-sections for the quotient map
$G\curvearrowright X$
on a finite-dimensional space X has finite Rokhlin dimension if and only if it is free. The case of global actions is implicit in [Reference Hirshberg and Phillips17], and it is an easy consequence of the existence of local cross-sections for the quotient map
![]() $\pi \colon X\to X/G$
. However, the proof in the partial setting is considerably more complicated, since even for free partial actions there may not exist local cross-sections for
$\pi \colon X\to X/G$
. However, the proof in the partial setting is considerably more complicated, since even for free partial actions there may not exist local cross-sections for
![]() $\pi $
. The proof in our context is quite involved and will occupy the entire section.
$\pi $
. The proof in our context is quite involved and will occupy the entire section.
Definition 5.1. Let X be a topological space. A topological partial action of a discrete group G on X is given by a pair
![]() $((X_g)_{g\in G}, (\theta _g)_{g\in G})$
, consisting of open subsets
$((X_g)_{g\in G}, (\theta _g)_{g\in G})$
, consisting of open subsets
![]() $X_g\subseteq X$
and homeomorphisms
$X_g\subseteq X$
and homeomorphisms
![]() $\theta _g\colon X_{g^{-1}}\to X_g$
, satisfying
$\theta _g\colon X_{g^{-1}}\to X_g$
, satisfying
-
(1)
 $X_1=X$
and
$X_1=X$
and
 $\theta _1={\mathrm {id}}_X$
; and
$\theta _1={\mathrm {id}}_X$
; and -
(2)
 $\theta _g\circ \theta _h\subseteq \theta _{gh}$
for all
$\theta _g\circ \theta _h\subseteq \theta _{gh}$
for all
 $g,h\in G$
.
$g,h\in G$
.
We say that
![]() $\theta $
is free if
$\theta $
is free if
![]() $\theta _{g}(x)\neq x$
for all
$\theta _{g}(x)\neq x$
for all
![]() $g\in G\setminus \{1_G\}$
and all
$g\in G\setminus \{1_G\}$
and all
![]() $x\in X_{g^{-1}}$
.
$x\in X_{g^{-1}}$
.
Next, we show that finite Rokhlin dimension implies freeness in the above setting.
Proposition 5.2. Let X be a locally compact Hausdorff space, let G be a finite group, let
![]() $\theta $
be a topological partial action of G on X, and denote by
$\theta $
be a topological partial action of G on X, and denote by
![]() $\alpha $
the induced partial action of G on
$\alpha $
the induced partial action of G on
![]() $C_0(X)$
. If
$C_0(X)$
. If
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
, then
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
, then
![]() $\theta $
is free.
$\theta $
is free.
Proof Set
![]() $d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
, and assume that
$d={\mathrm {dim}_{\mathrm {Rok}}}(\alpha )$
, and assume that
![]() $d<\infty $
. Let
$d<\infty $
. Let
![]() $g\in G\setminus \{1\}$
be given. Arguing by contradiction, assume that
$g\in G\setminus \{1\}$
be given. Arguing by contradiction, assume that
![]() $F_g=\{x\in X_{g^{-1}}\colon \theta _{g}(x)=x\}$
is not empty, and fix
$F_g=\{x\in X_{g^{-1}}\colon \theta _{g}(x)=x\}$
is not empty, and fix
![]() $x\in F_g$
. Note that x belongs to
$x\in F_g$
. Note that x belongs to
![]() $X_g\cap X_{g^{-1}}$
. Let
$X_g\cap X_{g^{-1}}$
. Let
![]() $a\in C_0(X_{g^{-1}})$
be a positive contraction satisfying
$a\in C_0(X_{g^{-1}})$
be a positive contraction satisfying
![]() $a(x)=1$
. Choose
$a(x)=1$
. Choose
![]() $\varepsilon>0$
with
$\varepsilon>0$
with
![]() $\varepsilon < ({1}/{2(|G|(d+1)+1)^2})$
, and let
$\varepsilon < ({1}/{2(|G|(d+1)+1)^2})$
, and let
![]() $f_h^{(j)}\in C_0(X_h)$
, for
$f_h^{(j)}\in C_0(X_h)$
, for
![]() $h\in G$
, and
$h\in G$
, and
![]() $j=0,\ldots , d$
be Rokhlin towers for
$j=0,\ldots , d$
be Rokhlin towers for
![]() $(\{a, \alpha _g(a)\},\varepsilon )$
. Given
$(\{a, \alpha _g(a)\},\varepsilon )$
. Given
![]() $h\in G$
and
$h\in G$
and
![]() $j=0,\ldots ,d$
, we have:
$j=0,\ldots ,d$
, we have:
 $$ \begin{align*} \|f_h^{(j)}\alpha_g(f_h^{(j)}a)\|_\infty&\leq \|f_h^{(j)}(\underbrace{\alpha_g(f_h^{(j)}a)-f_{gh}^{(j)}\alpha_g(a)}_{\ \ \ \approx_\varepsilon 0})\|_\infty+ \|\underbrace{f_h^{(j)}f_{gh}^{(j)}}_{ \ \ \ \approx_\varepsilon 0}\alpha_g(a)\|_\infty<2\varepsilon. \end{align*} $$
$$ \begin{align*} \|f_h^{(j)}\alpha_g(f_h^{(j)}a)\|_\infty&\leq \|f_h^{(j)}(\underbrace{\alpha_g(f_h^{(j)}a)-f_{gh}^{(j)}\alpha_g(a)}_{\ \ \ \approx_\varepsilon 0})\|_\infty+ \|\underbrace{f_h^{(j)}f_{gh}^{(j)}}_{ \ \ \ \approx_\varepsilon 0}\alpha_g(a)\|_\infty<2\varepsilon. \end{align*} $$
Evaluating at x, we get
Since
![]() $\theta _{g^{-1}}(x)=x$
and
$\theta _{g^{-1}}(x)=x$
and
![]() $a(x)=1$
, we deduce that
$a(x)=1$
, we deduce that
for all
![]() $h\in G$
and
$h\in G$
and
![]() $j=0,\ldots ,d$
. Moreover, condition (3) from Definition 2.1 gives
$j=0,\ldots ,d$
. Moreover, condition (3) from Definition 2.1 gives
 $$ \begin{align*} \bigg|\sum\limits_{j=0}^{d}\sum\limits_{h\in G}f_h^{(j)}(x)a(x)-a(x)\bigg|\stackrel{a(x)=1}{=}\bigg|\sum\limits_{j=0}^{d}\sum\limits_{h\in G}f_h^{(j)}(x)-1\bigg|<\varepsilon,\end{align*} $$
$$ \begin{align*} \bigg|\sum\limits_{j=0}^{d}\sum\limits_{h\in G}f_h^{(j)}(x)a(x)-a(x)\bigg|\stackrel{a(x)=1}{=}\bigg|\sum\limits_{j=0}^{d}\sum\limits_{h\in G}f_h^{(j)}(x)-1\bigg|<\varepsilon,\end{align*} $$
so
![]() $\sum \nolimits _{j=0}^{d}\sum \nolimits _{h\in G}f_h^{(j)}(x)>1-\varepsilon $
. Using this at the second step, we get
$\sum \nolimits _{j=0}^{d}\sum \nolimits _{h\in G}f_h^{(j)}(x)>1-\varepsilon $
. Using this at the second step, we get
 $$ \begin{align*}|G|(d+1)\sqrt{2\varepsilon}\stackrel{(5.1)}{>}\sum\limits_{j=0}^{d}\sum\limits_{g\in G}f_g^{(j)}(x) >1-\varepsilon\geq 1-\sqrt{2\varepsilon}.\end{align*} $$
$$ \begin{align*}|G|(d+1)\sqrt{2\varepsilon}\stackrel{(5.1)}{>}\sum\limits_{j=0}^{d}\sum\limits_{g\in G}f_g^{(j)}(x) >1-\varepsilon\geq 1-\sqrt{2\varepsilon}.\end{align*} $$
This contradicts the choice of
![]() $\varepsilon $
, showing that
$\varepsilon $
, showing that
![]() $F_g$
is empty. Thus
$F_g$
is empty. Thus
![]() $\theta $
is free.
$\theta $
is free.
The rest of the section will be devoted to proving that free partial actions have finite Rokhlin dimension. The general strategy is as follows.
-
Step 1: Show that free decomposable partial actions have finite Rokhlin dimension.
-
Step 2: Show that an extension of topological partial actions with finite Rokhlin dimension again has finite Rokhlin dimension.
-
Step 3: Use the equivariant decomposition into successive extensions from Theorem 4.5 to conclude that the given action has finite Rokhlin dimension.
Using the results we proved in §4, we can easily establish the first step.
Proposition 5.3. Let G be a finite group, let
![]() $n\in \{1,\ldots ,|G|\}$
, let X be a locally compact space with
$n\in \{1,\ldots ,|G|\}$
, let X be a locally compact space with
![]() $\dim (X)<\infty $
, and let
$\dim (X)<\infty $
, and let
![]() $\sigma $
be a partial action of G on X with the n-decomposition property (see Definition
4.2
). Denote by
$\sigma $
be a partial action of G on X with the n-decomposition property (see Definition
4.2
). Denote by
![]() $\alpha $
the induced partial action of G on
$\alpha $
the induced partial action of G on
![]() $C_0(X)$
. If
$C_0(X)$
. If
![]() $\sigma $
is free, then
$\sigma $
is free, then
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq \dim (X)$
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq \dim (X)$
.
Proof Fix
![]() $\tau \in \mathcal {T}_n(G)$
. Then
$\tau \in \mathcal {T}_n(G)$
. Then
![]() $X_\tau $
is an open subset of X and thus
$X_\tau $
is an open subset of X and thus
![]() $\dim (X_\tau )\leq \dim (X)$
. By part (2) of Theorem 5.4 in [Reference Abadie, Gardella and Geffen2], the restricted global action of
$\dim (X_\tau )\leq \dim (X)$
. By part (2) of Theorem 5.4 in [Reference Abadie, Gardella and Geffen2], the restricted global action of
![]() $H_\tau $
on
$H_\tau $
on
![]() $X_\tau $
is free. Using Proposition 2.11 in [Reference Hirshberg and Phillips17] at the first step, it follows that
$X_\tau $
is free. Using Proposition 2.11 in [Reference Hirshberg and Phillips17] at the first step, it follows that
Thus, the result follows from Theorem 4.6.
Step 2 is considerably more complicated. Roughly speaking, one needs to lift Rokhlin towers from the quotient to the algebra, while at the same time respecting the domains of the partial action. If we did not care about respecting the domains (such as in the global case), the result would be an immediate consequence of the fact that the cone of
![]() ${\mathbb {C}}^n$
is projective. In our setting, the greatest difficulty lies in showing that this can be done in a way compatible with the domains, and for this we will need some lemmas that allow us to assume that the Rokhlin towers and their lifts are orthogonal; see Lemma 5.4 and Lemma 5.5. It is unclear whether these results hold without assuming that the algebra is commutative.
${\mathbb {C}}^n$
is projective. In our setting, the greatest difficulty lies in showing that this can be done in a way compatible with the domains, and for this we will need some lemmas that allow us to assume that the Rokhlin towers and their lifts are orthogonal; see Lemma 5.4 and Lemma 5.5. It is unclear whether these results hold without assuming that the algebra is commutative.
First, we show that for partial actions on commutative unital
![]() $C^*$
-algebras, the elements of each Rokhlin tower can be assumed to be exactly orthogonal.
$C^*$
-algebras, the elements of each Rokhlin tower can be assumed to be exactly orthogonal.
Lemma 5.4. Let
![]() $\alpha $
be a partial action of a finite group G on a unital, commutative
$\alpha $
be a partial action of a finite group G on a unital, commutative
![]() $C^*$
-algebra A, and let
$C^*$
-algebra A, and let
![]() $d\in {\mathbb {N}}$
. Then
$d\in {\mathbb {N}}$
. Then
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
if and only if for all
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq d$
if and only if for all
![]() $\varepsilon>0$
and every finite subset
$\varepsilon>0$
and every finite subset
![]() $F\subseteq A$
there exist positive contractions
$F\subseteq A$
there exist positive contractions
![]() $f_g^{(j)}\in A_g$
, for
$f_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying:
$j=0,\ldots ,d$
, satisfying:
-
(1)
 $\| \alpha _g(f_h^{(j)}a)- f_{gh}^{(j)}\alpha _g(a)\|<\varepsilon $
for all
$\| \alpha _g(f_h^{(j)}a)- f_{gh}^{(j)}\alpha _g(a)\|<\varepsilon $
for all
 $a\in F\cap A_{g^{-1}}$
;
$a\in F\cap A_{g^{-1}}$
; -
(2)
 $f_g^{(j)}f_h^{(j)}=0$
for all
$f_g^{(j)}f_h^{(j)}=0$
for all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
and for all
$g\neq h$
and for all
 $j=0,\ldots ,d$
;
$j=0,\ldots ,d$
; -
(3)
 $\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d}f_g^{(j)}-1\|<\varepsilon $
.
$\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d}f_g^{(j)}-1\|<\varepsilon $
.
Proof It is clear that any action satisfying conditions (1), (2), and (3) in the statement has Rokhlin dimension at most d (the approximate commutation condition from Definition 2.1 is vacuous since A is commutative). We therefore prove the non-trivial implication. Let
![]() $\varepsilon>0$
and let a finite subset
$\varepsilon>0$
and let a finite subset
![]() $F\subseteq A$
be given. Without loss of generality, we assume that F consists of positive contractions.
$F\subseteq A$
be given. Without loss of generality, we assume that F consists of positive contractions.
Fix
![]() $\varepsilon _0<1$
such that
$\varepsilon _0<1$
such that
![]() $(d+2)|G|^2\sqrt {\varepsilon _0}<\varepsilon $
, and choose positive contractions
$(d+2)|G|^2\sqrt {\varepsilon _0}<\varepsilon $
, and choose positive contractions
![]() $x_g^{(j)}\in A_g$
, for
$x_g^{(j)}\in A_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, satisfying:
$j=0,\ldots ,d$
, satisfying:
-
(a)
 $\| \alpha _g(x_h^{(j)}a)- x_{gh}^{(j)}\alpha _g(a)\|<\varepsilon _0$
for all
$\| \alpha _g(x_h^{(j)}a)- x_{gh}^{(j)}\alpha _g(a)\|<\varepsilon _0$
for all
 $a\in F\cap A_{g^{-1}}$
;
$a\in F\cap A_{g^{-1}}$
; -
(b)
 $\|x_g^{(j)}x_h^{(j)}\|<\varepsilon _0$
for all
$\|x_g^{(j)}x_h^{(j)}\|<\varepsilon _0$
for all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
and for all
$g\neq h$
and for all
 $j=0,\ldots ,d$
;
$j=0,\ldots ,d$
; -
(c)
 $\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d}x_g^{(j)}-1\|<\varepsilon _0$
.
$\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d}x_g^{(j)}-1\|<\varepsilon _0$
.
For
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
, set
$j=0,\ldots ,d$
, set
![]() $y_g^{(j)}=\sum \nolimits _{h\in G\setminus \{g\}}x_h^{(j)}$
and
$y_g^{(j)}=\sum \nolimits _{h\in G\setminus \{g\}}x_h^{(j)}$
and
Since A is commutative, we have
![]() $f_g^{(j)}\leq x_g^{(j)}$
and hence
$f_g^{(j)}\leq x_g^{(j)}$
and hence
![]() $f_g^{(j)}$
is a positive contraction in
$f_g^{(j)}$
is a positive contraction in
![]() $A_g$
. We will show that these elements satisfy the conditions in the statement. We begin by noting that the
$A_g$
. We will show that these elements satisfy the conditions in the statement. We begin by noting that the
![]() $f_g^{(j)}$
are very close to the
$f_g^{(j)}$
are very close to the
![]() $x_g^{(j)}$
.
$x_g^{(j)}$
.
Claim.
We have
![]() $\|x_g^{(j)}-f_g^{(j)}\|< |G|\sqrt {\varepsilon _0}$
for all
$\|x_g^{(j)}-f_g^{(j)}\|< |G|\sqrt {\varepsilon _0}$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
. To see this, since A is abelian, it is enough to prove that
$j=0,\ldots ,d$
. To see this, since A is abelian, it is enough to prove that
![]() $|x_g^{(j)}(t)-f_g^{(j)}(t)|\leq |G|\sqrt {\varepsilon _0}$
for every
$|x_g^{(j)}(t)-f_g^{(j)}(t)|\leq |G|\sqrt {\varepsilon _0}$
for every
![]() $t\in \mathrm {Spec}(A)$
. Fix
$t\in \mathrm {Spec}(A)$
. Fix
![]() $t\in \mathrm {Spec}(A)$
. We divide the proof into two cases.
$t\in \mathrm {Spec}(A)$
. We divide the proof into two cases.
Suppose that
![]() $x_g^{(j)}(t)\geq y^{(j)}_g(t)$
. Then
$x_g^{(j)}(t)\geq y^{(j)}_g(t)$
. Then
![]() $f_g^{(j)}(t)=x^{(j)}_g(t)-y_g^{(j)}(t)$
and hence
$f_g^{(j)}(t)=x^{(j)}_g(t)-y_g^{(j)}(t)$
and hence
 $$ \begin{align} x_g^{(j)}(t)-f_g^{(j)}(t)=y_g^{(j)}(t)=\sum\limits_{h\in G\setminus\{g\}}x_h^{(j)}(t).\end{align} $$
$$ \begin{align} x_g^{(j)}(t)-f_g^{(j)}(t)=y_g^{(j)}(t)=\sum\limits_{h\in G\setminus\{g\}}x_h^{(j)}(t).\end{align} $$
For
![]() $h\neq g$
, we have
$h\neq g$
, we have
![]() $x_h^{(j)}(t)\leq y_g^{(j)}(t)\leq x_g^{(j)}(t)$
, and thus
$x_h^{(j)}(t)\leq y_g^{(j)}(t)\leq x_g^{(j)}(t)$
, and thus
We conclude that
 $$ \begin{align*}|x_g^{(j)}(t)-f_g^{(j)}(t)| \stackrel{({5.2})}{\leq} \sum_{h\in G\setminus\{g\}}|x_h^{(j)}(t)| \stackrel{({5.3})}{<} (|G|-1)\sqrt{\varepsilon_0}< |G|\sqrt{\varepsilon_0}.\end{align*} $$
$$ \begin{align*}|x_g^{(j)}(t)-f_g^{(j)}(t)| \stackrel{({5.2})}{\leq} \sum_{h\in G\setminus\{g\}}|x_h^{(j)}(t)| \stackrel{({5.3})}{<} (|G|-1)\sqrt{\varepsilon_0}< |G|\sqrt{\varepsilon_0}.\end{align*} $$
Suppose that
![]() $x_g^{(j)}(t)\leq y^{(j)}_g(t)$
. Then
$x_g^{(j)}(t)\leq y^{(j)}_g(t)$
. Then
![]() $f_g^{(j)}(t)=0$
and hence
$f_g^{(j)}(t)=0$
and hence
![]() $x_g^{(j)}(t)-f_g^{(j)}(t)=x_g^{(j)}(t)$
. Moreover,
$x_g^{(j)}(t)-f_g^{(j)}(t)=x_g^{(j)}(t)$
. Moreover,
 $$ \begin{align} x_g^{(j)}(t)^2\leq \bigg(\sum\limits_{h\in G\setminus\{g\}}x_h^{(j)}(t)\bigg)x_g^{(j)}(t)\stackrel{\mathrm{(b)}}{\leq} (|G|-1)\varepsilon_0.\end{align} $$
$$ \begin{align} x_g^{(j)}(t)^2\leq \bigg(\sum\limits_{h\in G\setminus\{g\}}x_h^{(j)}(t)\bigg)x_g^{(j)}(t)\stackrel{\mathrm{(b)}}{\leq} (|G|-1)\varepsilon_0.\end{align} $$
Thus,
This proves the claim.
We check that the positive contractions
![]() $f_g^{(j)}$
for
$f_g^{(j)}$
for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d$
satisfy conditions (1), (2), and (3) in the statement. Conditions (1) and (3) follow immediately by combining the claim above with conditions (a) and (c), respectively, so we only check (2). Let
$j=0,\ldots ,d$
satisfy conditions (1), (2), and (3) in the statement. Conditions (1) and (3) follow immediately by combining the claim above with conditions (a) and (c), respectively, so we only check (2). Let
![]() $g,h\in G$
with
$g,h\in G$
with
![]() $g\neq h$
and let
$g\neq h$
and let
![]() $j=0,\ldots ,d$
. Using the inequalities
$j=0,\ldots ,d$
. Using the inequalities
![]() $x_g^{(j)}\leq y_h^{(j)}$
and
$x_g^{(j)}\leq y_h^{(j)}$
and
![]() $x_h^{(j)}\leq y_g^{(j)}$
(which are valid since
$x_h^{(j)}\leq y_g^{(j)}$
(which are valid since
![]() $g\neq h$
) at the second step, and the identity
$g\neq h$
) at the second step, and the identity
![]() $(z-w)_+(w-z)_+=0$
at the last step, we get
$(z-w)_+(w-z)_+=0$
at the last step, we get
 $$ \begin{align*} f_g^{(j)}f_h^{(j)}&= (x_g^{(j)}-y_g^{(j)})_+(x_h^{(j)}-y_h^{(j)})_+\\ &\leq (y_h^{(j)}-y_g^{(j)})_+(y_g^{(j)}-y_h^{(j)})_+=0. \\[-34pt] \end{align*} $$
$$ \begin{align*} f_g^{(j)}f_h^{(j)}&= (x_g^{(j)}-y_g^{(j)})_+(x_h^{(j)}-y_h^{(j)})_+\\ &\leq (y_h^{(j)}-y_g^{(j)})_+(y_g^{(j)}-y_h^{(j)})_+=0. \\[-34pt] \end{align*} $$
The following lemma deals with obtaining domain-respecting orthogonal lifts.
Lemma 5.5. Let A be a commutative
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $n\in {\mathbb {N}}$
, and let
$n\in {\mathbb {N}}$
, and let
![]() $J, A_1,\ldots , A_n$
be ideals in A. We set
$J, A_1,\ldots , A_n$
be ideals in A. We set
![]() $B=A/J$
with quotient map
$B=A/J$
with quotient map
![]() $\pi \colon A\to B$
, and
$\pi \colon A\to B$
, and
 $$ \begin{align*}B_j=\frac{A_j}{A_j\cap J}\cong \frac{A_j+J}{J}\end{align*} $$
$$ \begin{align*}B_j=\frac{A_j}{A_j\cap J}\cong \frac{A_j+J}{J}\end{align*} $$
for
![]() $j=1,\ldots ,n$
. For
$j=1,\ldots ,n$
. For
![]() $j=1,\ldots ,n$
, let
$j=1,\ldots ,n$
, let
![]() $x_j\in A_j$
be a positive contraction satisfying
$x_j\in A_j$
be a positive contraction satisfying
![]() $x_jx_k\in J$
for all
$x_jx_k\in J$
for all
![]() $k=1,\ldots ,n$
with
$k=1,\ldots ,n$
with
![]() $j\neq k$
. Then there exist pairwise orthogonal positive contractions
$j\neq k$
. Then there exist pairwise orthogonal positive contractions
![]() $y_j\in A_j$
, for
$y_j\in A_j$
, for
![]() $j=1,\ldots ,n$
, satisfying
$j=1,\ldots ,n$
, satisfying
![]() $\pi (y_j)=\pi (x_j)$
.
$\pi (y_j)=\pi (x_j)$
.
Proof We prove the lemma by induction on n, the case
![]() $n=1$
being trivial. Assume that
$n=1$
being trivial. Assume that
![]() $n=2$
, and let
$n=2$
, and let
![]() $x_1\in A_1$
and
$x_1\in A_1$
and
![]() $x_2\in A_2$
be positive contractions satisfying
$x_2\in A_2$
be positive contractions satisfying
![]() $x_1x_2\in J$
. Set
$x_1x_2\in J$
. Set
![]() $y_1=(x_1-x_2)_+$
and
$y_1=(x_1-x_2)_+$
and
![]() $y_2=(x_2-x_1)_+$
, which are positive contractions. Since A is abelian, we have
$y_2=(x_2-x_1)_+$
, which are positive contractions. Since A is abelian, we have
![]() $y_j\leq x_j$
and hence
$y_j\leq x_j$
and hence
![]() $y_j$
belongs to
$y_j$
belongs to
![]() $A_j$
for
$A_j$
for
![]() $j=1,2$
. Moreover,
$j=1,2$
. Moreover,
![]() $y_1y_2=0$
. Finally, using at the first step that
$y_1y_2=0$
. Finally, using at the first step that
![]() $\pi (x_1)\pi (x_2)=0$
, we get
$\pi (x_1)\pi (x_2)=0$
, we get
Similarly,
![]() $\pi (x_2)=\pi (y_2)$
. This proves the case
$\pi (x_2)=\pi (y_2)$
. This proves the case
![]() $n=2$
of the statement.
$n=2$
of the statement.
Assume now that we have proved the result for an integer
![]() $n\geq 2$
, and let us prove it for
$n\geq 2$
, and let us prove it for
![]() $n+1$
. Thus, let
$n+1$
. Thus, let
![]() $A_1,\ldots , A_{n+1}$
be ideals in A, and let
$A_1,\ldots , A_{n+1}$
be ideals in A, and let
![]() $x_1,\ldots , x_{n+1}$
be as in the statement. Set
$x_1,\ldots , x_{n+1}$
be as in the statement. Set
![]() $x=\sum _{j=1}^n x_j$
and define
$x=\sum _{j=1}^n x_j$
and define
![]() $y_{n+1}=(x_{n+1}-x)_+$
. Then
$y_{n+1}=(x_{n+1}-x)_+$
. Then
![]() $y_{n+1}$
is a positive contraction with
$y_{n+1}$
is a positive contraction with
![]() $y_{n+1}\leq x_{n+1}$
, and hence
$y_{n+1}\leq x_{n+1}$
, and hence
![]() $y_{n+1}\in A_{n+1}$
. Moreover, since
$y_{n+1}\in A_{n+1}$
. Moreover, since
![]() $\pi (x)\pi (x_{n+1})=0$
and using the same argument as in the case
$\pi (x)\pi (x_{n+1})=0$
and using the same argument as in the case
![]() $n=2$
, it follows that
$n=2$
, it follows that
![]() $\pi (y_{n+1})=\pi (x_{n+1})$
.
$\pi (y_{n+1})=\pi (x_{n+1})$
.
For
![]() $j=1,\ldots ,n$
, set
$j=1,\ldots ,n$
, set
![]() $z_j=(x_j-x_{n+1})_+$
, which is a positive contraction in
$z_j=(x_j-x_{n+1})_+$
, which is a positive contraction in
![]() $A_j$
with
$A_j$
with
![]() $z_j\leq x_j$
. Since
$z_j\leq x_j$
. Since
![]() $\pi (x_j)\pi (x_{n+1})=0$
for
$\pi (x_j)\pi (x_{n+1})=0$
for
![]() $j\leq n$
, it follows that
$j\leq n$
, it follows that
![]() $\pi (z_j)=\pi (x_j)$
. In particular, for
$\pi (z_j)=\pi (x_j)$
. In particular, for
![]() $1\leq j\neq k\leq n$
we have
$1\leq j\neq k\leq n$
we have
![]() $\pi (z_jz_k)=0$
, that is,
$\pi (z_jz_k)=0$
, that is,
![]() $z_jz_k \in J$
. By the inductive step applied to
$z_jz_k \in J$
. By the inductive step applied to
![]() $z_1,\ldots ,z_n$
, there exist orthogonal positive contractions
$z_1,\ldots ,z_n$
, there exist orthogonal positive contractions
![]() $y_j\leq z_j$
, for
$y_j\leq z_j$
, for
![]() $j=1,\ldots ,n$
, satisfying
$j=1,\ldots ,n$
, satisfying
![]() $\pi (y_j)=\pi (z_j)$
. Then
$\pi (y_j)=\pi (z_j)$
. Then
![]() $y_j\leq x_j$
and
$y_j\leq x_j$
and
![]() $\pi (y_j)=\pi (x_j)$
for
$\pi (y_j)=\pi (x_j)$
for
![]() $j=1,\ldots ,n+1$
. It remains to prove that the
$j=1,\ldots ,n+1$
. It remains to prove that the
![]() $y_1,\ldots ,y_{n+1}$
are pairwise orthogonal. By construction, the contractions
$y_1,\ldots ,y_{n+1}$
are pairwise orthogonal. By construction, the contractions
![]() $y_1,\ldots , y_n$
are pairwise orthogonal, so it suffices to check orthogonality with
$y_1,\ldots , y_n$
are pairwise orthogonal, so it suffices to check orthogonality with
![]() $y_{n+1}$
. For
$y_{n+1}$
. For
![]() $j=1,\ldots ,n$
, we have
$j=1,\ldots ,n$
, we have
using at the third step that A is commutative and
![]() $x\geq x_j$
.
$x\geq x_j$
.
We are now ready to prove that an extension of partial actions on commutative
![]() $C^*$
-algebras with finite Rokhlin dimension again has finite Rokhlin dimension. For use in this proof, we recall the following standard fact. Let A be a unital
$C^*$
-algebras with finite Rokhlin dimension again has finite Rokhlin dimension. For use in this proof, we recall the following standard fact. Let A be a unital
![]() $C^*$
-algebra, let J be an ideal in A, let
$C^*$
-algebra, let J be an ideal in A, let
![]() $\pi \colon A\to A/J$
denote the quotient map, let
$\pi \colon A\to A/J$
denote the quotient map, let
![]() $(e_\lambda )_{\lambda \in \Lambda }$
be any approximate identity for J, and let
$(e_\lambda )_{\lambda \in \Lambda }$
be any approximate identity for J, and let
![]() $a\in A$
. Then
$a\in A$
. Then
![]() $\|\pi (a)\|=\limsup \nolimits _{\lambda \in \Lambda }\|a(1-e_\lambda )\|$
.
$\|\pi (a)\|=\limsup \nolimits _{\lambda \in \Lambda }\|a(1-e_\lambda )\|$
.
Proposition 5.6. Let G be a finite group, let A be a commutative unital
![]() $C^*$
-algebra, let
$C^*$
-algebra, let
![]() $\alpha $
be a partial action of G on A, and let J be an
$\alpha $
be a partial action of G on A, and let J be an
![]() $\alpha $
-invariant ideal in A with a G-invariant approximate identity. Denote by
$\alpha $
-invariant ideal in A with a G-invariant approximate identity. Denote by
![]() $\overline {\alpha }$
the induced partial action of G on
$\overline {\alpha }$
the induced partial action of G on
![]() $A/J$
as in Proposition
2.6
. Then
$A/J$
as in Proposition
2.6
. Then
Proof Set
![]() $d_1={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_J)$
and
$d_1={\mathrm {dim}_{\mathrm {Rok}}}(\alpha |_J)$
and
![]() $d_2={\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })$
. Without loss of generality, we assume that
$d_2={\mathrm {dim}_{\mathrm {Rok}}}(\overline {\alpha })$
. Without loss of generality, we assume that
![]() $d_1,d_2<\infty $
. Let
$d_1,d_2<\infty $
. Let
![]() $\varepsilon>0$
and let
$\varepsilon>0$
and let
![]() $F\subseteq A$
be a finite subset. We abbreviate
$F\subseteq A$
be a finite subset. We abbreviate
![]() $B=A/J$
and
$B=A/J$
and
![]() $B_g= A_g/(A_g\cap J)$
for all
$B_g= A_g/(A_g\cap J)$
for all
![]() $g\in G$
. We denote by
$g\in G$
. We denote by
![]() $\pi \colon A\to B$
the canonical quotient map. We use Lemma 5.4 to choose positive contractions
$\pi \colon A\to B$
the canonical quotient map. We use Lemma 5.4 to choose positive contractions
![]() $x_g^{(j)}\in B_g$
, for
$x_g^{(j)}\in B_g$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots , d_2$
, satisfying:
$j=0,\ldots , d_2$
, satisfying:
-
(B.1)
 $\| \overline {\alpha }_g(x_h^{(j)}b)- x_{gh}^{(j)}\overline {\alpha }_g(b)\|<\varepsilon $
for all
$\| \overline {\alpha }_g(x_h^{(j)}b)- x_{gh}^{(j)}\overline {\alpha }_g(b)\|<\varepsilon $
for all
 $g,h\in G$
, for all
$g,h\in G$
, for all
 $j=0,\ldots ,d_2$
, and for all
$j=0,\ldots ,d_2$
, and for all
 $b\in \pi (F)\cap B_{g^{-1}}$
;
$b\in \pi (F)\cap B_{g^{-1}}$
; -
(B.2)
 $x_g^{(j)}x_h^{(j)}=0$
for all
$x_g^{(j)}x_h^{(j)}=0$
for all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
and for all
$g\neq h$
and for all
 $j=0,\ldots ,d_2$
;
$j=0,\ldots ,d_2$
; -
(B.3)
 $\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d_2}x_g^{(j)}-1\|<\varepsilon $
.
$\|\!\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d_2}x_g^{(j)}-1\|<\varepsilon $
.
Fix
![]() $j=0,\ldots ,d_2$
. Use Lemma 5.5 to find mutually orthogonal positive contractions
$j=0,\ldots ,d_2$
. Use Lemma 5.5 to find mutually orthogonal positive contractions
![]() $y_g^{(j)}\in A_g$
, for
$y_g^{(j)}\in A_g$
, for
![]() $g\in G$
, satisfying
$g\in G$
, satisfying
![]() $\pi (y^{(j)}_g)=x_g^{(j)}$
. Using that J has a G-invariant approximate identity, find a positive contraction
$\pi (y^{(j)}_g)=x_g^{(j)}$
. Using that J has a G-invariant approximate identity, find a positive contraction
![]() $q\in J$
satisfying:
$q\in J$
satisfying:
-
(a)
 $\alpha _g(qx)=q\alpha _g(x)$
for all
$\alpha _g(qx)=q\alpha _g(x)$
for all
 $x\in A_{g^{-1}}\cap J$
;
$x\in A_{g^{-1}}\cap J$
; -
(b)
 $\| (1-\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d} y_g^{(j)})(1-q)\|<\varepsilon $
;
$\| (1-\sum \nolimits _{g\in G}\sum \nolimits _{j=0}^{d} y_g^{(j)})(1-q)\|<\varepsilon $
; -
(c)
 $\| (\alpha _g(y_h^{(j)}a)-y_{gh}^{(j)}\alpha _g(a))(1-q)\|<\varepsilon $
for all
$\| (\alpha _g(y_h^{(j)}a)-y_{gh}^{(j)}\alpha _g(a))(1-q)\|<\varepsilon $
for all
 $a\in A_{g^{-1}}\cap F$
.
$a\in A_{g^{-1}}\cap F$
.
Claim.
![]() $\alpha _g(qa)=q\alpha _g(a)$
for all
$\alpha _g(qa)=q\alpha _g(a)$
for all
![]() $a\in A_{g^{-1}}$
. To prove this, let
$a\in A_{g^{-1}}$
. To prove this, let
![]() $(e_\lambda )_{\lambda \in \Lambda }$
be an approximate identity for
$(e_\lambda )_{\lambda \in \Lambda }$
be an approximate identity for
![]() $A_{g^{-1}}\cap J$
. Then
$A_{g^{-1}}\cap J$
. Then
![]() $(\alpha _g(e_\lambda ))_{\lambda \in \Lambda }$
is an approximate identity for
$(\alpha _g(e_\lambda ))_{\lambda \in \Lambda }$
is an approximate identity for
![]() $A_g\cap J$
. Fix
$A_g\cap J$
. Fix
![]() $a\in A_{g^{-1}}$
. In the next computation, we use at the third step condition (a) above with
$a\in A_{g^{-1}}$
. In the next computation, we use at the third step condition (a) above with
![]() $x=ae_\lambda $
, and the fact that
$x=ae_\lambda $
, and the fact that
![]() $qa$
belongs to
$qa$
belongs to
![]() $A_{g^{-1}}\cap J$
at the fourth step:
$A_{g^{-1}}\cap J$
at the fourth step:
This proves the claim.
Set
![]() $z_g^{(j)}=y_g^{(j)}(1-q)$
for
$z_g^{(j)}=y_g^{(j)}(1-q)$
for
![]() $g\in G$
and
$g\in G$
and
![]() $j=0,\ldots ,d_2$
. Then
$j=0,\ldots ,d_2$
. Then
for
![]() $g,h\in G$
with
$g,h\in G$
with
![]() $g\neq h$
and for
$g\neq h$
and for
![]() $j=0,\ldots ,d_2$
, since
$j=0,\ldots ,d_2$
, since
![]() $1-q$
is central. Let
$1-q$
is central. Let
![]() $g,h\in G$
, let
$g,h\in G$
, let
![]() $a\in F\cap A_{g^{-1}}$
, and let
$a\in F\cap A_{g^{-1}}$
, and let
![]() $j=0,\ldots ,d_2$
be given. Using the above claim at the second step, we get
$j=0,\ldots ,d_2$
be given. Using the above claim at the second step, we get
Furthermore,
 $$ \begin{align}\bigg\|\sum\limits_{g\in G}\sum\limits_{j=0}^{d_2}z_g^{(j)}-(1-q)\bigg\|<\varepsilon. \end{align} $$
$$ \begin{align}\bigg\|\sum\limits_{g\in G}\sum\limits_{j=0}^{d_2}z_g^{(j)}-(1-q)\bigg\|<\varepsilon. \end{align} $$
Set
![]() $F_J=\{qa\colon a\in F\}\cup \{q\}\subseteq J$
. Choose positive contractions
$F_J=\{qa\colon a\in F\}\cup \{q\}\subseteq J$
. Choose positive contractions
![]() $\xi _g^{(k)}\in A_g\cap J$
, for
$\xi _g^{(k)}\in A_g\cap J$
, for
![]() $g\in G$
and
$g\in G$
and
![]() $k=0,\ldots , d_1$
, satisfying:
$k=0,\ldots , d_1$
, satisfying:
-
(J.1)
 $\| \alpha _g(\xi _h^{(k)}c)- \xi _{gh}^{(k)}\alpha _g(c)\|<\varepsilon $
for all
$\| \alpha _g(\xi _h^{(k)}c)- \xi _{gh}^{(k)}\alpha _g(c)\|<\varepsilon $
for all
 $g,h\in G$
, for all
$g,h\in G$
, for all
 $k=0,\ldots ,d_1$
, and for all
$k=0,\ldots ,d_1$
, and for all
 $c\in F_J\cap J_{g^{-1}}$
;
$c\in F_J\cap J_{g^{-1}}$
; -
(J.2)
 $\|\xi _g^{(k)}\xi _h^{(k)}c\|<\varepsilon $
for all
$\|\xi _g^{(k)}\xi _h^{(k)}c\|<\varepsilon $
for all
 $g,h\in G$
with
$g,h\in G$
with
 $g\neq h$
, for all
$g\neq h$
, for all
 $k=0,\ldots ,d_1$
, and for all
$k=0,\ldots ,d_1$
, and for all
 $c\in F_J$
;
$c\in F_J$
; -
(J.3)
 $\|c-c(\sum \nolimits _{g\in G}\sum \nolimits _{k=0}^{d_1}\xi _g^{(k)})\|<\varepsilon $
for all
$\|c-c(\sum \nolimits _{g\in G}\sum \nolimits _{k=0}^{d_1}\xi _g^{(k)})\|<\varepsilon $
for all
 $c\in F_J$
.
$c\in F_J$
.
Set
![]() $\eta _g^{(k)}=\xi _g^{(k)}q$
for all
$\eta _g^{(k)}=\xi _g^{(k)}q$
for all
![]() $g\in G$
and
$g\in G$
and
![]() $k=0,\ldots , d_1$
. For
$k=0,\ldots , d_1$
. For
![]() $a\in F\cap A_{g^{-1}}$
, we have
$a\in F\cap A_{g^{-1}}$
, we have
because
![]() $qa\in J_{g^{-1}}\cap F_J$
. Since q is central (because A is commutative), we have
$qa\in J_{g^{-1}}\cap F_J$
. Since q is central (because A is commutative), we have
for
![]() $g,h\in G$
with
$g,h\in G$
with
![]() $g\neq h$
and for
$g\neq h$
and for
![]() $k=0,\ldots ,d_1$
. Further, taking
$k=0,\ldots ,d_1$
. Further, taking
![]() $c=q$
in (J.3) gives
$c=q$
in (J.3) gives
 $$ \begin{align} \bigg\| \sum\limits_{g\in G}\sum\limits_{k=0}^{d_1} \eta_g^{(k)}-q\bigg\| \leq \varepsilon. \end{align} $$
$$ \begin{align} \bigg\| \sum\limits_{g\in G}\sum\limits_{k=0}^{d_1} \eta_g^{(k)}-q\bigg\| \leq \varepsilon. \end{align} $$
For
![]() $g\in G$
and
$g\in G$
and
![]() $\ell =0,\ldots ,d_1+d_2+1$
, set
$\ell =0,\ldots ,d_1+d_2+1$
, set
 $$ \begin{align*}f_g^{(j)} = \left. \begin{cases} z_g^{(j)} & \text{for } \ell=0,\ldots,d_2, \\ \eta_g^{(\ell-d_2-1)} & \text{for } \ell=d_2+1,d_2+2,\ldots,d_1+d_2+1. \end{cases} \right.\end{align*} $$
$$ \begin{align*}f_g^{(j)} = \left. \begin{cases} z_g^{(j)} & \text{for } \ell=0,\ldots,d_2, \\ \eta_g^{(\ell-d_2-1)} & \text{for } \ell=d_2+1,d_2+2,\ldots,d_1+d_2+1. \end{cases} \right.\end{align*} $$
Then
![]() $\{f_g^{(j)}\colon g\in G, 0\leq \ell \leq d_1+d_2+1\}$
are Rokhlin towers for
$\{f_g^{(j)}\colon g\in G, 0\leq \ell \leq d_1+d_2+1\}$
are Rokhlin towers for
![]() $\alpha $
with respect to
$\alpha $
with respect to
![]() $(F,2\varepsilon )$
. Indeed, condition (1) follows from (5.5) and (5.8); condition (2) follows from (5.6) and (5.9); and condition (3) follows from (5.7) and (5.10).
$(F,2\varepsilon )$
. Indeed, condition (1) follows from (5.5) and (5.8); condition (2) follows from (5.6) and (5.9); and condition (3) follows from (5.7) and (5.10).
For technical reasons it will be more convenient to work with unital
![]() $C^*$
-algebras. In order to reduce to the unital case, we define the minimal partial unitization of a partial action. This unitization differs from the usual unitization of a global action, since the minimal partial unitization is never a global action, even if the original action was. For a
$C^*$
-algebras. In order to reduce to the unital case, we define the minimal partial unitization of a partial action. This unitization differs from the usual unitization of a global action, since the minimal partial unitization is never a global action, even if the original action was. For a
![]() $C^*$
-algebra A, we denote by
$C^*$
-algebra A, we denote by
![]() $A^+$
the unitization of A, which as a Banach space is isomorphic to
$A^+$
the unitization of A, which as a Banach space is isomorphic to
![]() $A\oplus {\mathbb {C}}$
.
$A\oplus {\mathbb {C}}$
.
Definition 5.7. Let G be a locally compact group, let A be a
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha =((A_g)_{g\in G}, (\alpha _g)_{g\in G})$
be a partial action of G on A. We define the minimal partial unitization
$\alpha =((A_g)_{g\in G}, (\alpha _g)_{g\in G})$
be a partial action of G on A. We define the minimal partial unitization
![]() $\alpha ^+$
of
$\alpha ^+$
of
![]() $\alpha $
to be the partial action of G on
$\alpha $
to be the partial action of G on
![]() $A^+$
determined by
$A^+$
determined by
![]() $A^+_g=A_g$
and
$A^+_g=A_g$
and
![]() $\alpha ^+_g=\alpha _g$
for all
$\alpha ^+_g=\alpha _g$
for all
![]() $g\in G\setminus \{1\}$
.
$g\in G\setminus \{1\}$
.
For later use, we record the following easy observation.
Remark 5.8. Let G be a finite group, let A be a commutative
![]() $C^*$
-algebra, and let
$C^*$
-algebra, and let
![]() $\alpha $
be a partial action of G on A. Then
$\alpha $
be a partial action of G on A. Then
![]() $(A,\alpha )$
is an equivariant ideal in
$(A,\alpha )$
is an equivariant ideal in
![]() $(A^+,\alpha ^+)$
, and hence
$(A^+,\alpha ^+)$
, and hence
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^+)$
by Proposition 2.6.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^+)$
by Proposition 2.6.
For a partial action
![]() $\theta $
of a group G on a locally compact space X, one defines its minimal partial compactification
$\theta $
of a group G on a locally compact space X, one defines its minimal partial compactification
![]() $\theta ^+$
analogously to Definition 5.7, only by compactifying the domain of the identity element and leaving the rest unchanged. It is clear that the partial action of G on
$\theta ^+$
analogously to Definition 5.7, only by compactifying the domain of the identity element and leaving the rest unchanged. It is clear that the partial action of G on
![]() $C(X^+)$
induced by
$C(X^+)$
induced by
![]() $\theta ^+$
can be canonically identified by the minimal partial unitization of the partial action induced by
$\theta ^+$
can be canonically identified by the minimal partial unitization of the partial action induced by
![]() $\theta $
.
$\theta $
.
One feature of the minimal partial unitization, in comparison with the unitization in the sense of global actions, is that the minimal partial unitization of a free action on a locally compact space is again free, as we show next. On the other hand, the unitization (in the global sense) of a free action is never free, since the point at infinity is necessarily fixed.
Lemma 5.9. Let G be a locally compact group, let X be a locally compact Hausdorff space, and let
![]() $\theta =((X_g)_{g\in G}, (\theta _g)_{g\in G})$
be a partial action of G on X. Then
$\theta =((X_g)_{g\in G}, (\theta _g)_{g\in G})$
be a partial action of G on X. Then
![]() $\theta $
is free if and only if
$\theta $
is free if and only if
![]() $\theta ^+$
is free.
$\theta ^+$
is free.
Proof It is clear that
![]() $\theta $
is free if
$\theta $
is free if
![]() $\theta ^+$
is free. Conversely, and arguing by contradiction, let
$\theta ^+$
is free. Conversely, and arguing by contradiction, let
![]() $g\in G\setminus \{1\}$
and
$g\in G\setminus \{1\}$
and
![]() $x\in X_{g^{-1}}^+$
satisfy
$x\in X_{g^{-1}}^+$
satisfy
![]() $\theta ^+_g(x)=x$
. Since
$\theta ^+_g(x)=x$
. Since
![]() $g\neq 1$
, this implies that
$g\neq 1$
, this implies that
![]() $x\in X_{g^{-1}}$
and
$x\in X_{g^{-1}}$
and
![]() $\theta _g(x)=x$
, which contradicts the fact that
$\theta _g(x)=x$
, which contradicts the fact that
![]() $\theta $
is free, as desired.
$\theta $
is free, as desired.
We have now arrived at the main result of this section.
Theorem 5.10. Let G be a finite group, let X be a locally compact space with
![]() $\dim (X)<\infty $
, let
$\dim (X)<\infty $
, let
![]() $\theta $
be a partial action of G on X, and let
$\theta $
be a partial action of G on X, and let
![]() $\alpha $
denote the partial action of G on
$\alpha $
denote the partial action of G on
![]() $C_0(X)$
induced by
$C_0(X)$
induced by
![]() $\theta $
. If
$\theta $
. If
![]() $\theta $
is free, then
$\theta $
is free, then
Proof We begin with a general fact.
Claim. Let
![]() $\beta $
be a free partial action of G on a unital commutative
$\beta $
be a free partial action of G on a unital commutative
![]() $C^*$
-algebra B with finite-dimensional spectrum. Suppose that there is an equivariant extension
$C^*$
-algebra B with finite-dimensional spectrum. Suppose that there is an equivariant extension
with
![]() $\delta $
decomposable and
$\delta $
decomposable and
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\gamma )<\infty $
. Then
${\mathrm {dim}_{\mathrm {Rok}}}(\gamma )<\infty $
. Then
By Proposition 4.4 in [Reference Abadie, Gardella and Geffen2],
![]() $(D,\delta )$
admits a G-invariant approximate identity. Since B is unital and commutative, by Proposition 5.6, we have
$(D,\delta )$
admits a G-invariant approximate identity. Since B is unital and commutative, by Proposition 5.6, we have
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\delta )+{\mathrm {dim}_{\mathrm {Rok}}}(\gamma )+1$
, so it suffices to show that
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )\leq {\mathrm {dim}_{\mathrm {Rok}}}(\delta )+{\mathrm {dim}_{\mathrm {Rok}}}(\gamma )+1$
, so it suffices to show that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\delta )$
is finite. Since
${\mathrm {dim}_{\mathrm {Rok}}}(\delta )$
is finite. Since
![]() $\beta $
is free, it is easy to see that so is
$\beta $
is free, it is easy to see that so is
![]() $\delta $
. Since
$\delta $
. Since
![]() $\delta $
is decomposable, the claim follows from Proposition 5.3.
$\delta $
is decomposable, the claim follows from Proposition 5.3.
We now prove the theorem. We will obtain the bound for
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^+)$
, which is enough by Remark 5.8. Since
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha ^+)$
, which is enough by Remark 5.8. Since
![]() $\alpha ^+$
is free by Lemma 5.9, upon replacing
$\alpha ^+$
is free by Lemma 5.9, upon replacing
![]() $\alpha $
with
$\alpha $
with
![]() $\alpha ^+$
we may assume that X is compact. By Theorem 6.1 in [Reference Abadie, Gardella and Geffen2], there are canonical equivariant extensions
$\alpha ^+$
we may assume that X is compact. By Theorem 6.1 in [Reference Abadie, Gardella and Geffen2], there are canonical equivariant extensions
for
![]() $2\leq k \leq |G|$
, satisfying the following properties:
$2\leq k \leq |G|$
, satisfying the following properties:
-
(1)
 $A^{(|G|)}=C(X)$
and
$A^{(|G|)}=C(X)$
and
 $\alpha ^{|G|}=\alpha $
;
$\alpha ^{|G|}=\alpha $
; -
(2)
 $\delta ^{(k)}$
has the k-decomposition property;
$\delta ^{(k)}$
has the k-decomposition property; -
(3)
 $\alpha ^{(1)}$
has the 1-decomposition property.
$\alpha ^{(1)}$
has the 1-decomposition property.
Note that all the partial actions involved are free (this is shown inductively, using that restrictions of free actions are free). Moreover,
![]() $A^{(k)}$
is unital and commutative for all
$A^{(k)}$
is unital and commutative for all
![]() $k=2,\ldots ,|G|$
. Note that
$k=2,\ldots ,|G|$
. Note that
![]() $\alpha ^{(1)}$
has Rokhlin dimension zero by Example 2.2. Applying the above claim to the extension in (5.11) with
$\alpha ^{(1)}$
has Rokhlin dimension zero by Example 2.2. Applying the above claim to the extension in (5.11) with
![]() $k=2$
, we get
$k=2$
, we get
Continuing inductively, after
![]() $|G|-1$
steps we deduce that
$|G|-1$
steps we deduce that
Suppose now that
![]() $\dim (X)$
is finite. For
$\dim (X)$
is finite. For
![]() $k=2,\ldots ,|G|$
, let
$k=2,\ldots ,|G|$
, let
![]() $Y_k$
denote the spectrum of
$Y_k$
denote the spectrum of
![]() $D^{(k)}$
. Since
$D^{(k)}$
. Since
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\delta ^{(k)})\leq \dim (Y_k)$
by Proposition 5.3, and
${\mathrm {dim}_{\mathrm {Rok}}}(\delta ^{(k)})\leq \dim (Y_k)$
by Proposition 5.3, and
![]() $\dim (Y_k)\leq \dim (X)$
, the dimensional estimate in the statement follows from (5.12).
$\dim (Y_k)\leq \dim (X)$
, the dimensional estimate in the statement follows from (5.12).
For clopen partial actions (that is, partial actions with clopen domains), no dimensionality assumptions on X are needed.
Proposition 5.11. Let G be a finite group, let X be a (not necessarily finite-dimensional) compact Hausdorff space, let
![]() $\theta $
be a free clopen partial action of G on X, and let
$\theta $
be a free clopen partial action of G on X, and let
![]() $\alpha $
denote the induced partial action of G on
$\alpha $
denote the induced partial action of G on
![]() $C(X)$
. Then
$C(X)$
. Then
In particular,
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
even if
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
even if
![]() $\dim (X)=\infty $
.
$\dim (X)=\infty $
.
Proof Denote by
![]() $(C(Y),\beta )$
the globalization of
$(C(Y),\beta )$
the globalization of
![]() $(C(X),\alpha )$
; see Proposition 3.5 in [Reference Abadie1], noting that the graph of
$(C(X),\alpha )$
; see Proposition 3.5 in [Reference Abadie1], noting that the graph of
![]() $\theta $
is closed. Note that
$\theta $
is closed. Note that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
by Theorem 3.4. Let
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )={\mathrm {dim}_{\mathrm {Rok}}}(\beta )$
by Theorem 3.4. Let
![]() $\sigma $
denote the action of G on Y induced by
$\sigma $
denote the action of G on Y induced by
![]() $\beta $
.
$\beta $
.
We claim that
![]() $\sigma $
is free. Note that
$\sigma $
is free. Note that
![]() $Y=\bigcup _{g\in G}\sigma _g(X)$
. Let
$Y=\bigcup _{g\in G}\sigma _g(X)$
. Let
![]() $g\in G$
and
$g\in G$
and
![]() $y\in Y$
satisfy
$y\in Y$
satisfy
![]() $\sigma _g(y)=y$
. Choose
$\sigma _g(y)=y$
. Choose
![]() $h\in G$
and
$h\in G$
and
![]() $x\in X$
such that
$x\in X$
such that
![]() $y=\sigma _h(x)$
, so that
$y=\sigma _h(x)$
, so that
![]() $\sigma _{h^{-1}gh}(x)=x$
. Thus x belongs to
$\sigma _{h^{-1}gh}(x)=x$
. Thus x belongs to
![]() $X\cap \sigma _{h^{-1}gh}(X)=X_{h^{-1}gh}$
, which is where
$X\cap \sigma _{h^{-1}gh}(X)=X_{h^{-1}gh}$
, which is where
![]() $\sigma _{hgh^{-1}}$
agrees with
$\sigma _{hgh^{-1}}$
agrees with
![]() $\theta _{hgh^{-1}}$
. Thus
$\theta _{hgh^{-1}}$
. Thus
![]() $\theta _{hgh^{-1}}(x)=x$
, and since
$\theta _{hgh^{-1}}(x)=x$
, and since
![]() $\theta $
is free, this implies that
$\theta $
is free, this implies that
![]() $hgh^{-1}=1_G$
and hence also
$hgh^{-1}=1_G$
and hence also
![]() $g=1_G$
. Hence
$g=1_G$
. Hence
![]() $\sigma $
is free.
$\sigma $
is free.
Since Y is compact, it follows from Theorem 4.2 in [Reference Gardella11] that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\beta )<\infty $
, and thus
${\mathrm {dim}_{\mathrm {Rok}}}(\beta )<\infty $
, and thus
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
.
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )<\infty $
.
We complete the proof by showing that
![]() ${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq \dim (X)$
. Note that
${\mathrm {dim}_{\mathrm {Rok}}}(\alpha )\leq \dim (X)$
. Note that
![]() $\dim (Y)=\dim (X)$
(this follows, for example, by the claim in the proof of Theorem 4.10). Using [Reference Hirshberg and Phillips17, Lemma 1.9] at the second step, we get
$\dim (Y)=\dim (X)$
(this follows, for example, by the claim in the proof of Theorem 4.10). Using [Reference Hirshberg and Phillips17, Lemma 1.9] at the second step, we get
Acknowledgments
The second named author was partially supported by the Deutsche Forschungsgemeinschaft’s (DFG, German Research Foundation) eigene Stelle, and by a Postdoctoral Research Fellowship from the Humboldt Foundation. The third named author was supported by a Kreitman Foundation Fellowship, a Minerva Fellowship Programme, and by an Israel Science Foundation grant no. 476/16. The second and third named authors were partially supported by the DFG through SFB 878 and under Germany’s Excellence Strategy EXC 2044–390685587, Mathematics Münster–Dynamics–Geometry–Structure, and also by ERC Advanced Grant 834267–AMAREC.