Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-25T19:44:15.547Z Has data issue: false hasContentIssue false
  • English
  • Français

Parameter rigid actions of simply connected nilpotent Lie groups

Published online by Cambridge University Press:  22 August 2012

HIROKAZU MARUHASHI
HIROKAZU MARUHASHI*
Affiliation:
Department of Mathematics, Kyoto University, Japan (email: [email protected])
Get access Rights & Permissions [Opens in a new window]

Abstract

We show that for a locally free 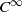$C^{\infty }$-action of a connected and simply connected nilpotent Lie group on a compact manifold, if every real-valued cocycle is cohomologous to a constant cocycle, then the action is parameter rigid. The converse is true if the action has a dense orbit. Using this, we construct parameter rigid actions of simply connected nilpotent Lie groups whose Lie algebras admit rational structures with graduations. This generalizes the results of dos Santos [Parameter rigid actions of the Heisenberg groups. Ergod. Th. & Dynam. Sys.27(2007), 1719–1735] concerning the Heisenberg groups.

Type
Research Article
Information
Ergodic Theory and Dynamical Systems , Volume 33 , Issue 6 , December 2013 , pp. 1864 - 1875
Copyright
Copyright © 2012 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

[1]Asaoka, M.. Deformation of locally free actions and the leafwise cohomology. arXiv:1012.2946.Google Scholar
[2]Corwin, L. and Greenleaf, F. P.. Representations of Nilpotent Lie Groups and Their Applications. Part 1:Basic Theory and Examples (Cambridge Studies in Advanced Mathematics, 18). Cambridge University Press, Cambridge, 1990.Google Scholar
[3]Katok, A. and Spatzier, R. J.. First cohomology of Anosov actions of higher rank abelian groups and applications to rigidity. Publ. Math. Inst. Hautes Études Sci. 79 (1994), 131–156.CrossRefGoogle Scholar
[4]Matsumoto, S. and Mitsumatsu, Y.. Leafwise cohomology and rigidity of certain Lie group actions. Ergod. Th. & Dynam. Sys. 23 (2003), 1839–1866.Google Scholar
[5]Mieczkowski, D.. The first cohomology of parabolic actions for some higher-rank abelian groups and representation theory. J. Mod. Dyn. 1 (2007), 61–92.Google Scholar
[6]Pereira, M. S. and dos Santos, N. M.. On the cohomology of foliated bundles. Proyecciones 21(2) (2002), 175–197.Google Scholar
[7]Ramírez, F. A.. Cocycles over higher-rank abelian actions on quotients of semisimple Lie groups. J. Mod. Dyn. 3 (2009), 335–357.CrossRefGoogle Scholar
[8]dos Santos, N. M.. Parameter rigid actions of the Heisenberg groups. Ergod. Th. & Dynam. Sys. 27 (2007), 1719–1735.Google Scholar