No CrossRef data available.
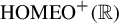 ${\textup {HOMEO}}^+(\mathbb R)$
${\textup {HOMEO}}^+(\mathbb R)$Published online by Cambridge University Press: 29 April 2021
We consider random walks on the group of orientation-preserving homeomorphisms of the real line
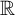 ${\mathbb R}$
. In particular, the fundamental question of uniqueness of an invariant measure of the generated process is raised. This problem was studied by Choquet and Deny [Sur l’équation de convolution
${\mathbb R}$
. In particular, the fundamental question of uniqueness of an invariant measure of the generated process is raised. This problem was studied by Choquet and Deny [Sur l’équation de convolution
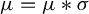 $\mu = \mu * \sigma $
. C. R. Acad. Sci. Paris250 (1960), 799–801] in the context of random walks generated by translations of the line. Nowadays the answer is quite well understood in general settings of strongly contractive systems. Here we focus on a broader class of systems satisfying the conditions of recurrence, contraction and unbounded action. We prove that under these conditions the random process possesses a unique invariant Radon measure on
$\mu = \mu * \sigma $
. C. R. Acad. Sci. Paris250 (1960), 799–801] in the context of random walks generated by translations of the line. Nowadays the answer is quite well understood in general settings of strongly contractive systems. Here we focus on a broader class of systems satisfying the conditions of recurrence, contraction and unbounded action. We prove that under these conditions the random process possesses a unique invariant Radon measure on
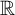 ${\mathbb R}$
. Our work can be viewed as following on from Babillot et al [The random difference equation
${\mathbb R}$
. Our work can be viewed as following on from Babillot et al [The random difference equation
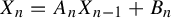 $X_n=A_n X_{n-1}+B_n$
in the critical case. Ann. Probab.25(1) (1997), 478–493] and Deroin et al [Symmetric random walk on
$X_n=A_n X_{n-1}+B_n$
in the critical case. Ann. Probab.25(1) (1997), 478–493] and Deroin et al [Symmetric random walk on
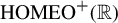 $\mathrm {HOMEO}^{+}(\mathbb {R})$
. Ann. Probab.41(3B) (2013), 2066–2089].
$\mathrm {HOMEO}^{+}(\mathbb {R})$
. Ann. Probab.41(3B) (2013), 2066–2089].