Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T06:15:49.806Z Has data issue: false hasContentIssue false
  • English
  • Français

On uniform distribution of polynomials and good universality

Published online by Cambridge University Press:  10 August 2018

RADHAKRISHNAN NAIR  and
ENTESAR NASR
RADHAKRISHNAN NAIR
Affiliation:
Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK email [email protected], [email protected]
ENTESAR NASR
Affiliation:
Mathematical Sciences, University of Liverpool, Liverpool L69 7ZL, UK email [email protected], [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Suppose $(k_{n})_{n\geq 1}$ is Hartman uniformly distributed and good universal. Also suppose 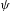$\unicode[STIX]{x1D713}$ is a polynomial with at least one coefficient other than 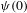$\unicode[STIX]{x1D713}(0)$ an irrational number. We adapt an argument due to Furstenberg to prove that the sequence 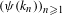$(\unicode[STIX]{x1D713}(k_{n}))_{n\geq 1}$ is uniformly distributed modulo one. This is used to give some new families of Poincaré recurrent sequences. In addition we show these sequences are also intersective and Glasner.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 40 , Issue 4 , April 2020 , pp. 992 - 1007
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Cambridge University Press, 2018

References

Ajtai, M., Havas, I. and Komlós, J.. Every group admits a bad topology. Studies in Pure Mathematics. Eds. Erdös, P., Alpár, L., Halász, G. and Sárközy, A.. Birkhäuser, Basel, 1983, pp. 21–34.Google Scholar
Alon, N. and Peres, Y.. Uniform dilations. Geom. Funct. Anal. 2(1) (1992), 1–28.Google Scholar
Asmar, N. H. and Nair, R.. Certain averages on the a-adic numbers. Proc. Amer. Math. Soc. 114(1) (1992), 21–28.Google Scholar
Bellow, A. and Losert, V.. On sequences of zero density in ergodic theory. Conference in Modern Analysis and Probability (New Haven, CT 1982) (Contemporary Mathematics, 26). American Mathematical Society, Providence, RI, 1984, pp. 49–60.Google Scholar
Berend, D. and Peres, Y.. Asymptotically dense dilations of sets on the circle. J. Lond. Math. Soc. (2) 47(1) (1993), 1–17.Google Scholar
Bergelson, V., Kolesnik, G., Madritsch, M., Son, Y. and Tichy, R.. Uniform distribution of prime powers and sets of recurrence and van der Corput sets in ℤk. Israel J. Math. 201(2) (2014), 729–760.Google Scholar
Bergelson, V. and Leibman, A.. A Weyl-type equidistribution theorem in finite characteristic. Adv. Math. 289 (2016), 928–950.Google Scholar
Bergelson, V. and Lesigne, E.. Van der Corput sets in ℤd. Colloq. Math. 110(1) (2008), 1–49.Google Scholar
Bertrand-Mathis, A.. Ensembles intersectifs et récurrence de Poincaré. Israel J. Math. 55(2) (1986), 184–198.Google Scholar
Blum, J. and Eisenberg, B.. Generalized summing sequences and the mean ergodic theorem. Proc. Amer. Math. Soc. 42 (1974), 423–429.Google Scholar
Boshernitzan, M.. Homogeneously distributed sequences and Poincaré sequences of integers of sublacunary growth. Monatsh. Math. 96(3) (1983), 173–181.Google Scholar
Boshernitzan, M., Kolesnik, G., Quas, A. and Wierdl, M.. Ergodic averaging sequences. J. Anal. Math. 95 (2005), 63–103.Google Scholar
Bourgain, J.. On the maximal ergodic theorem for certain subsets of the integers. Israel J. Math. 61(1) (1988), 39–72.Google Scholar
Drmota, M. and Tichy, R. F.. Sequences, Discrepancies and Applications (Lecture Notes in Mathematics, 1651). Springer, Berlin, 1997.Google Scholar
Furstenberg, H.. Strict ergodicity and transformation of the torus. Amer. J. Math. 83 (1961), 573–601.Google Scholar
Furstenberg, H.. Poincaré recurrence and number theory. Bull. Amer. Math. Soc. (N.S.) 5(3) (1981), 211–234.Google Scholar
Glasner, S.. Almost periodic sets and measures on the Torus. Israel J. Math. 32(2–3) (1979), 161–172.Google Scholar
Hua, L. K.. Sur une somme exponentielle. C. R. Acad. Sci. 210 (1940), 520–523.Google Scholar
Jaššová, A., Lertchoosakul, P. and Nair, R.. On variants of the Halton sequence. Monatsh. Math. 180(4) (2016), 743–764.Google Scholar
Kamarul Haili, H. and Nair, R.. On certain Glasner sets. Proc. Roy. Soc. Edinburgh Sect. A 133(4) (2003), 849–853.Google Scholar
Katznelson, Y.. An Introduction to Harmonic Analysis. Dover, New York, 1976.Google Scholar
Kristensen, S., Jaššová, A., Lertchoosakul, P. and Nair, R.. On recurrence in positive characteristic. Indag. Math. (N.S.) 26(2) (2015), 346–354.Google Scholar
Kuipers, L. and Niederreiter, H.. Uniform Distribution of Sequences. Wiley, New York, 1974.Google Scholar
Nair, R.. On certain solutions of the Diophantine equation x - y = p (z). Acta Arith. 62(1) (1992), 61–71.Google Scholar
Nair, R.. On polynomials in primes and J. Bourgain’s circle method approach to ergodic theorems II. Studia Math. 105(3) (1993), 207–233.Google Scholar
Nair, R.. On uniformly distributed sequences of integers and Poincaré recurrence. Indag. Math. (N.S.) 9(1) (1998), 55–63.Google Scholar
Nair, R.. On uniformly distributed sequences of integers and Poincaré recurrence II. Indag. Math. (N.S.) 9(3) (1998), 405–415.Google Scholar
Nair, R. and Velani, S. L.. Glasner sets and polynomials in primes. Proc. Amer. Math. Soc. 126(10) (1998), 2835–2840.Google Scholar
Nair, R. and Weber, M.. On random perturbation of some intersective set. Indag. Math. (N.S) 15(3) (2004), 373–381.Google Scholar
Oxtoby, J. C.. Ergodic sets. Bull. Amer. Math. Soc. 58 (1952), 116–136.Google Scholar
Sárközy, A.. On difference sets of sequences of integers. I. Acta Math. Acad. Sci. Hungar. 31(1–2) (1978), 125–149.Google Scholar
Sárközy, A.. On difference sets of sequences of integers. III. Acta Math. Acad. Sci. Hungar. 31(3–4) (1978), 355–386.Google Scholar
Sárközy, A.. On difference sets of sequences of integers. II. Ann. Univ. Sci. Budapest. Eötvös Sect. Math. 21 (1978), 45–53 (1979).Google Scholar
Sawyer, S.. Maximal inequalities of weak type. Ann. of Math. (2) 84 (1966), 157–174.Google Scholar
Thouvenot, J. P.. La convergence presque sûre des moyennes ergodiques suivant certaines sous-suites d’entiers (d’après Jean Bourgain), Séminaire Bourbaki, Vol. 1989/90. Astérisque 189–190 (1990), exp. no. 719, 133–153.Google Scholar
Urban, R. and Zienkiewicz, J.. Weak type (1,1) estimates for a class of discrete rough maximal functions. Math. Res. Lett. 14(2) (2007), 227–237.Google Scholar
Vaughan, R. C.. The Hardy–Littlewood Method (Cambridge Tracts in Mathematics, 125), 2nd edn. Cambridge University Press, Cambridge, 1997.Google Scholar
Viana, M. and Oliveira, K.. Foundations of Ergodic Theory (Cambridge Studies in Advanced Mathematics, 151). Cambridge University Press, Cambridge, 2016.Google Scholar
Weyl, H.. Über die Gleichverteilung von Zahlen mod. Eins. Math. Ann. 77(1) (1916), 313–352, Issue 3.Google Scholar