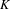Hostname: page-component-cd9895bd7-jn8rn Total loading time: 0 Render date: 2024-12-28T13:03:17.681Z Has data issue: false hasContentIssue false
  • English
  • Français

On the $K$-theory of 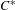$C^{\ast }$-algebras arising from integral dynamics

Published online by Cambridge University Press:  22 September 2016

SELÇUK BARLAK ,
TRON OMLAND  and
NICOLAI STAMMEIER
SELÇUK BARLAK
Affiliation:
Department of Mathematics and Computer Science, University of Southern Denmark, Campusvej 55, DK-5230 Odense M, Denmark email [email protected]
TRON OMLAND
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway email [email protected], [email protected]
NICOLAI STAMMEIER
Affiliation:
Department of Mathematics, University of Oslo, P.O. Box 1053 Blindern, NO-0316 Oslo, Norway email [email protected], [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate the 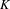$K$-theory of unital UCT Kirchberg algebras 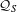${\mathcal{Q}}_{S}$ arising from families $S$ of relatively prime numbers. It is shown that 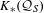$K_{\ast }({\mathcal{Q}}_{S})$ is the direct sum of a free abelian group and a torsion group, each of which is realized by another distinct 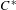$C^{\ast }$-algebra naturally associated to $S$. The 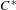$C^{\ast }$-algebra representing the torsion part is identified with a natural subalgebra 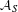${\mathcal{A}}_{S}$ of 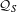${\mathcal{Q}}_{S}$. For the 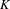$K$-theory of 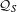${\mathcal{Q}}_{S}$, the cardinality of $S$ determines the free part and is also relevant for the torsion part, for which the greatest common divisor 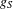$g_{S}$ of 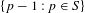$\{p-1:p\in S\}$ plays a central role as well. In the case where 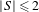$|S|\leq 2$ or 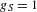$g_{S}=1$ we obtain a complete classification for 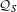${\mathcal{Q}}_{S}$. Our results support the conjecture that 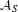${\mathcal{A}}_{S}$ coincides with 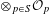$\otimes _{p\in S}{\mathcal{O}}_{p}$. This would lead to a complete classification of 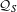${\mathcal{Q}}_{S}$, and is related to a conjecture about 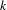$k$-graphs.

Type
Original Article
Information
Ergodic Theory and Dynamical Systems , Volume 38 , Issue 3 , May 2018 , pp. 832 - 862
Copyright
© Cambridge University Press, 2016 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Brownlowe, N., an Huef, A., Laca, M. and Raeburn, I.. Boundary quotients of the Toeplitz algebra of the affine semigroup over the natural numbers. Ergod. Th. & Dynam. Sys. 32(1) (2012), 35–62.Google Scholar
Barlak, S.. On the spectral sequence associated with the Baum–Connes conjecture for $\mathbb{Z}^{n}$ . Preprint, 2015, arXiv:1504.03298v2.Google Scholar
Barlak, S. and Szabó, G.. Sequentially split $\ast$ -homomorphisms between $C^{\ast }$ -algebras. Preprint, 2015, arXiv:1510.04555v2.Google Scholar
Bunce, J. W. and Deddens, J. A.. A family of simple C ∗ -algebras related to weighted shift operators. J. Funct. Anal. 19 (1975), 13–24.CrossRefGoogle Scholar
Brownlowe, N., Larsen, N. S. and Stammeier, N.. $C^{\ast }$ -algebras of algebraic dynamical systems and right LCM semigroups. Preprint, 2015, arXiv:1503.01599v1.Google Scholar
Brownlowe, N., Larsen, N. S. and Stammeier, N.. On C ∗ -algebras associated to right LCM semigroups. Trans. Amer. Math. Soc. published online 9 March 2016, doi:10.1090/tran/6638 (to appear in print).Google Scholar
Brownlowe, N., Ramagge, J., Robertson, D. and Whittaker, M. F.. Zappa–Szép products of semigroups and their C ∗ -algebras. J. Funct. Anal. 266(6) (2014), 3937–3967.CrossRefGoogle Scholar
Brownlowe, N. and Stammeier, N.. The boundary quotient for algebraic dynamical systems. J. Math. Anal. Appl. 438(2) (2016), 772–789.Google Scholar
Crisp, J. and Laca, M.. Boundary quotients and ideals of Toeplitz C ∗ -algebras of Artin groups. J. Funct. Anal. 242(1) (2007), 127–156.Google Scholar
Cuntz, J. and Li, X.. C ∗ -algebras associated with integral domains and crossed products by actions on adele spaces. J. Noncommut. Geom. 5(1) (2011), 1–37.Google Scholar
Combes, F.. Crossed products and Morita equivalence. Proc. Lond. Math. Soc. (3) 49(2) (1984), 289–306.Google Scholar
Cuntz, J.. C ∗ -algebras associated with the ax + b-semigroup over ℕ. K-theory and Noncommutative Geometry (EMS Series of Congress Reports) . European Mathematical Society, Zürich, 2008, pp. 201–215.Google Scholar
Cuntz, J.. A class of C ∗ -algebras and topological Markov chains II. Reducible chains and the Ext-functor for C ∗ -algebras. Invent. Math. 63 (1981), 25–40.Google Scholar
Cuntz, J. and Vershik, A.. C ∗ -algebras associated with endomorphisms and polymorphisms of compact abelian groups. Comm. Math. Phys. 321(1) (2013), 157–179.Google Scholar
Enders, D.. Semiprojectivity for Kirchberg algebras, Preprint, 2015, arXiv:1507.06091v1.Google Scholar
Evans, D. G.. On the K-theory of higher rank graph C ∗ -algebras. New York J. Math. 14 (2008), 1–31.Google Scholar
Fowler, N. J. and Sims, A.. Product systems over right-angled Artin semigroups. Trans. Amer. Math. Soc. 354(4) (2002), 1487–1509.Google Scholar
Glimm, J. G.. On a certain class of operator algebras. Trans. Amer. Math. Soc. 95 (1960), 318–340.Google Scholar
Hirshberg, I.. On C ∗ -algebras associated to certain endomorphisms of discrete groups. New York J. Math. 8 (2002), 99–109.Google Scholar
Hewitt, E. and Ross, K. A.. Abstract Harmonic Analysis. Vol. I (Grundlehren der Mathematischen Wissenschaften, 115) , 2nd edn. Springer, Berlin–New York, 1979.Google Scholar
Kasparov, G.. Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91(1) (1988), 147–201.Google Scholar
Katsura, T.. A class of C ∗ -algebras generalizing both graph algebras and homeomorphism C ∗ -algebras. IV. Pure infiniteness. J. Funct. Anal. 254(5) (2008), 1161–1187.Google Scholar
Kirchberg, E.. The Classification of Purely Infinite C ∗ -algebras Using Kasparov’s Theory (Fields Institute Communications) . American Mathematical Society, Providence, RI, to appear.Google Scholar
Kaliszewski, S., Omland, T. and Quigg, J.. Cuntz–Li algebras from a-adic numbers. Rev. Roumaine Math. Pures Appl. 59(3) (2014), 331–370.Google Scholar
Kumjian, A. and Pask, D.. Higher rank graph C ∗ -algebras. New York J. Math. 6 (2000), 1–20.Google Scholar
Laca, M.. From endomorphisms to automorphisms and back: dilations and full corners. J. Lond. Math. Soc. (2) 61(3) (2000), 893–904.Google Scholar
Li, X.. Semigroup C ∗ -algebras and amenability of semigroups. J. Funct. Anal. 262(10) (2012), 4302–4340.Google Scholar
Larsen, N. S. and Li, X.. The 2-adic ring C ∗ -algebra of the integers and its representations. J. Funct. Anal. 262(4) (2012), 1392–1426.Google Scholar
Li, X. and Norling, M. D.. Independent resolutions for totally disconnected dynamical systems II: C ∗ -algebraic case. J. Operator Theory 75(1) (2016), 163–193.Google Scholar
Loring, T. A.. Lifting Solutions to Perturbing Problems in C ∗ -algebras (Fields Institute Monographs, 8) . American Mathematical Society, Providence, RI, 1997.Google Scholar
Laca, M. and Raeburn, I.. Semigroup crossed products and the Toeplitz algebras of nonabelian groups. J. Funct. Anal. 139(2) (1996), 415–440.Google Scholar
Massey, W. S.. Exact couples in algebraic topology. I, II. Ann. of Math. (2) 56 (1952), 363–396.Google Scholar
Massey, W. S.. Exact couples in algebraic topology. III, IV, V. Ann. of Math. (2) 57 (1953), 248–286.Google Scholar
Nica, A.. C ∗ -algebras generated by isometries and Wiener–Hopf operators. J. Operator Theory 27(1) (1992), 17–52.Google Scholar
Omland, T.. C ∗ -algebras associated with a-adic numbers. Operator Algebra and Dynamics (Springer Proceedings in Mathematics and Statistics, 58) . Springer, Heidelberg, 2013, pp. 223–238.Google Scholar
Paschke, W. L.. K-theory for actions of the circle group on C ∗ -algebras. J. Operator Theory 6(1) (1981), 125–133.Google Scholar
Phillips, N. C.. A classification theorem for nuclear purely infinite simple C ∗ -algebras. Doc. Math. 5 (2000), 49–114.Google Scholar
Pimsner, M. V. and Voiculescu, D.-V.. Exact sequences for K-groups and Ext-groups of certain cross-product C ∗ -algebras. J. Operator Theory 4(1) (1980), 93–118.Google Scholar
Rørdam, M.. Classification of nuclear, simple C ∗ -algebras. Classification of Nuclear C ∗ -algebras. Entropy in Operator Algebras (Encyclopaedia of Mathematical Sciences, 126) . Springer, Berlin, 2002, pp. 1–145.Google Scholar
Raeburn, I. and Szymański, W.. Cuntz–Krieger algebras of infinite graphs and matrices. Trans. Amer. Math. Soc. 356(1) (2004), 39–59.CrossRefGoogle Scholar
Rosenberg, J. and Schochet, C.. The Künneth theorem and the universal coefficient theorem for Kasparov’s generalized K-functor. Duke Math. J. 55(2) (1987), 431–474.Google Scholar
Savinien, J. and Bellissard, J.. A spectral sequence for the K-theory of tiling spaces. Ergod. Th. & Dynam. Sys. 29(3) (2009), 997–1031.CrossRefGoogle Scholar
Schochet, C. L.. Topological methods for C ∗ -algebras. I. Spectral sequences. Pacific J. Math. 96(1) (1981), 193–211.Google Scholar
Stammeier, N.. A boundary quotient diagram for right LCM semigroups. Preprint, 2016, arXiv:1604.03172.Google Scholar
Stammeier, N.. On C ∗ -algebras of irreversible algebraic dynamical systems. J. Funct. Anal. 269(4) (2015), 1136–1179.Google Scholar
Williams, D. P.. Crossed Products of C ∗ -algebras (Mathematical Surveys and Monographs, 134) . American Mathematical Society, Providence, RI, 2007.Google Scholar
Zhang, S.. Certain C ∗ -algebras with real rank zero and their corona and multiplier algebras. I. Pacific J. Math. 155(1) (1992), 169–197.Google Scholar